Kiến thức về công thức va chạm mềm và các định luật bảo toàn cơ bản

Công thức va chạm mềm giúp giải quyết các bài toán về sự tương tác giữa các vật. Các định luật bảo toàn động lượng và cơ năng đóng vai trò then chốt trong quá trình va chạm. Bài viết phân tích chi tiết các trường hợp va chạm đàn hồi và không đàn hồi kèm ví dụ minh họa.

Công thức va chạm mềm trong vật lý

Va chạm mềm là hiện tượng phổ biến trong tự nhiên và đời sống. Đây là dạng va chạm không đàn hồi, động năng của hệ bị mất một phần do biến dạng vật chất.

Công thức va chạm mềm được xây dựng dựa trên định luật bảo toàn động lượng. Tôi thường giải thích cho học sinh bằng ví dụ hai viên bi sắt va chạm vào nhau rồi dính lại.

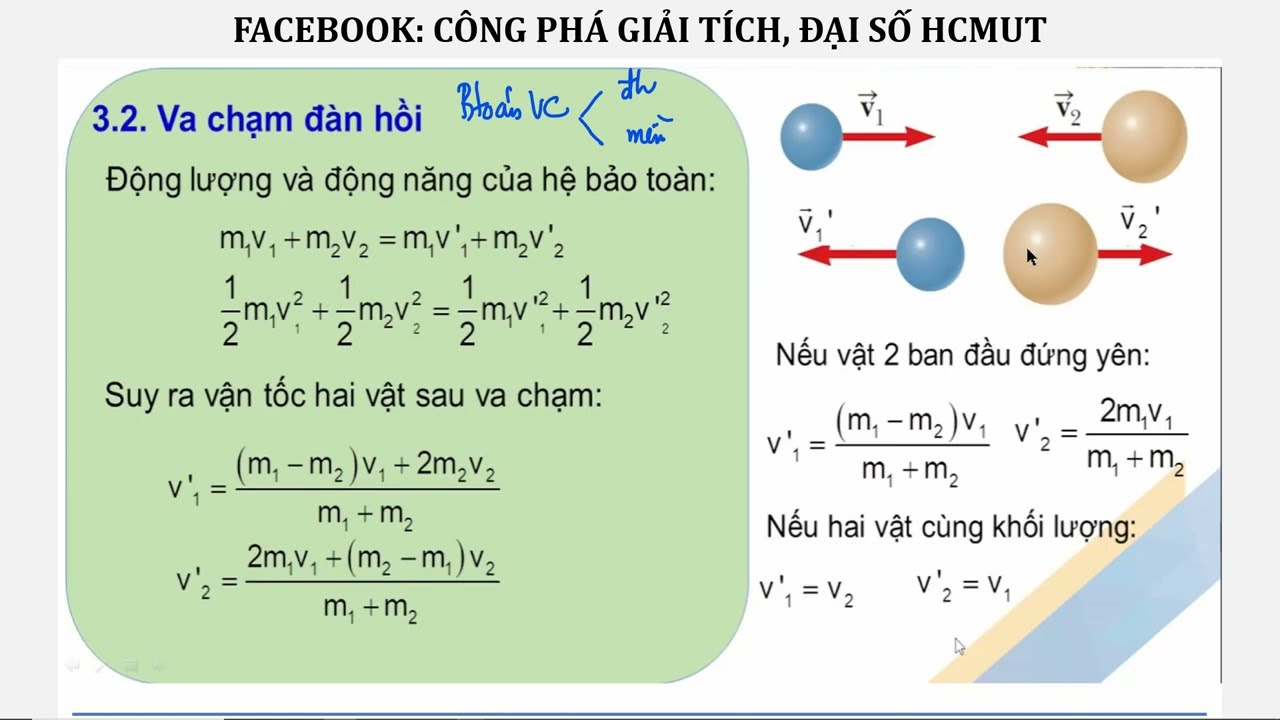
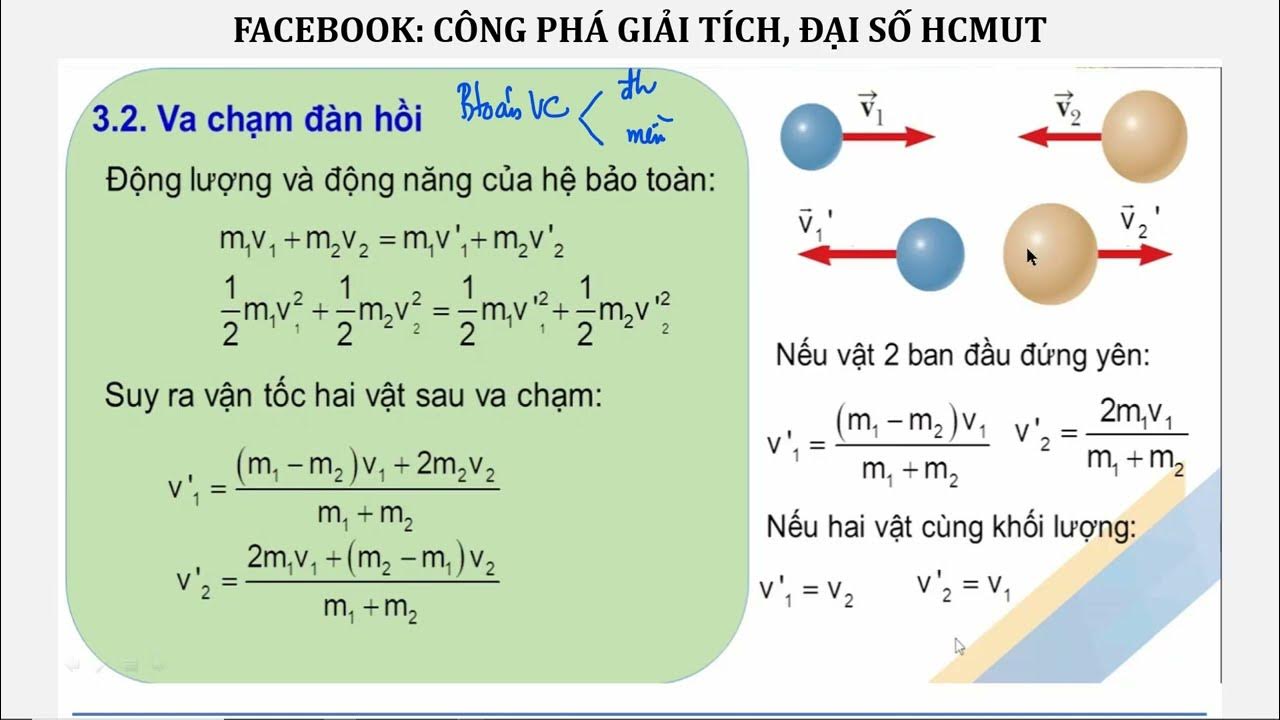
Công thức tổng quát:

m1v1 + m2v2 = (m1 + m2)v

Trong đó:

• m1, m2: khối lượng của vật 1 và vật 2 (kg)
• v1, v2: vận tốc ban đầu của vật 1 và vật 2 (m/s)
• v: vận tốc sau va chạm của khối lượng chung (m/s)

Một kinh nghiệm khi giải bài tập va chạm mềm là cần xác định rõ chiều chuyển động của các vật. Vận tốc cùng chiều mang dấu dương, ngược chiều mang dấu âm.

Ví dụ thực tế: Hai xe ô tô va chạm trực diện và dính chặt vào nhau. Đây là va chạm mềm điển hình, ta có thể áp dụng công thức trên để tính vận tốc sau va chạm của cả khối.

Lưu ý quan trọng khi sử dụng công thức: Động năng của hệ sau va chạm luôn nhỏ hơn tổng động năng ban đầu do có sự mất mát năng lượng trong quá trình va chạm.

Khái niệm và đặc điểm của va chạm mềm trong cơ học

Va chạm mềm là hiện tượng phổ biến trong cơ học, xảy ra khi hai vật tiếp xúc với nhau trong thời gian ngắn. Quá trình này làm thay đổi động lượng và động năng của các vật.

Trong va chạm mềm, các vật có thể biến dạng tạm thời hoặc vĩnh viễn. Điều này phụ thuộc vào tính chất vật liệu và năng lượng va chạm.

Va chạm mềm là gì và các trường hợp thường gặp

Va chạm mềm là quá trình hai vật tương tác trong đó có sự mất mát động năng do biến dạng hoặc ma sát. Đây là dạng va chạm phổ biến nhất trong thực tế.

Tôi thường lấy ví dụ về quả bóng tennis rơi xuống sân để học sinh dễ hình dung. Khi chạm sân, bóng bị biến dạng và nảy lên không cao bằng độ cao ban đầu.

Một trường hợp khác là va chạm giữa hai ô tô. Phần thân xe biến dạng hấp thụ một phần động năng, giúp giảm thiểu tác động lên người ngồi trong xe.

Phân biệt va chạm đàn hồi và va chạm không đàn hồi

Va chạm đàn hồi xảy ra khi động năng được bảo toàn hoàn toàn. Các vật chỉ biến dạng tạm thời và phục hồi nguyên trạng sau va chạm.

Va chạm không đàn hồi là trường hợp các vật dính vào nhau sau va chạm, động năng bị mất mát hoàn toàn do biến dạng. Bạn có thể tham khảo thêm về công thức va chạm đàn hồi để hiểu rõ hơn.

Hệ số phục hồi và ý nghĩa vật lý

Hệ số phục hồi k là đại lượng đặc trưng cho mức độ đàn hồi của va chạm, có giá trị từ 0 đến 1. Công thức tính:

k = |v2′

• v1’|/|v1 - v2|

Trong đó:

• v1, v2: vận tốc trước va chạm
• v1′, v2′: vận tốc sau va chạm

Hệ số k = 1 ứng với va chạm đàn hồi hoàn toàn, k = 0 ứng với va chạm không đàn hồi. Các va chạm thực tế thường có k nằm giữa 0 và 1.

Các định luật bảo toàn trong va chạm mềm

Va chạm mềm là hiện tượng hai vật va chạm vào nhau và dính lại thành một khối sau va chạm. Trong va chạm mềm, các định luật bảo toàn đóng vai trò quan trọng để phân tích chuyển động.

Các định luật này giúp ta hiểu được sự biến đổi về động lượng và năng lượng của hệ. Việc nắm vững các định luật sẽ giúp giải quyết nhiều bài toán phức tạp.

Định luật bảo toàn động lượng trong va chạm mềm

Định luật bảo toàn động lượng phát biểu rằng tổng động lượng của hệ trước và sau va chạm là không đổi. Công thức tổng quát:

m1v1 + m2v2 = (m1 + m2)v’

Trong đó:

• m1, m2: khối lượng của hai vật
• v1, v2: vận tốc trước va chạm
• v’: vận tốc chung sau va chạm

Qua 20 năm giảng dạy, tôi thường gợi ý học sinh hình dung như hai viên bi đất sét va chạm và dính vào nhau.

Định luật bảo toàn cơ năng và sự mất mát năng lượng

Trong va chạm mềm, định luật bảo toàn cơ năng không được bảo toàn hoàn toàn. Một phần năng lượng bị mất đi dưới dạng nhiệt và biến dạng.

Năng lượng mất mát được tính theo công thức:

ΔE = E1

• E2

E1 là năng lượng trước va chạm
E2 là năng lượng sau va chạm

Kinh nghiệm cho thấy học sinh dễ hiểu hơn khi so sánh với việc nắn đất sét

• năng lượng mất đi để làm biến dạng đất.

Mối quan hệ giữa động năng trước và sau va chạm

Động năng trước va chạm luôn lớn hơn động năng sau va chạm. Mối quan hệ được thể hiện qua công thức:

Wk1 = 1/2(m1v1² + m2v2²) > Wk2 = 1/2(m1 + m2)v’²

Sự chênh lệch này là do một phần động năng đã chuyển hóa thành nhiệt năng và năng lượng biến dạng trong quá trình va chạm.

Để minh họa, tôi thường cho học sinh thí nghiệm với hai viên bi đất sét

• sau va chạm chúng dính lại và chuyển động chậm hơn rõ rệt.

Phương pháp giải bài tập va chạm mềm

Va chạm mềm là hiện tượng hai vật va chạm vào nhau mà không giữ nguyên động năng. Việc nắm vững công thức va chạm mềm giúp giải quyết nhiều dạng bài tập phức tạp.

Khi giải các bài tập va chạm mềm, ta cần áp dụng định luật bảo toàn động lượng và tính đến sự mất mát động năng trong quá trình va chạm. Điều này khác với dao động cưỡng bức là gì vì không có ngoại lực tác động.

Các bước giải bài tập va chạm mềm cơ bản

Bước 1: Xác định vận tốc ban đầu của các vật trước va chạm
v1, v2 là vận tốc của vật 1 và vật 2 trước va chạm

Bước 2: Áp dụng định luật bảo toàn động lượng
m1v1 + m2v2 = m1u1 + m2u2
Trong đó u1, u2 là vận tốc sau va chạm

Bước 3: Sử dụng hệ số va chạm k
k = -(u2

• u1)/(v2 - v1)
  

Ví dụ minh họa và phân tích chi tiết

Hai vật khối lượng m1 = 2kg và m2 = 3kg chuyển động ngược chiều với vận tốc v1 = 4m/s và v2 = -2m/s. Sau va chạm, hệ số k = 0,5.

Áp dụng bảo toàn động lượng:
2×4 + 3×(-2) = 2u1 + 3u2

Thay k = 0,5 vào công thức:
0,5 = -(u2

• u1)/[(-2) - 4]

Giải hệ phương trình ta được:
u1 = -0,4 m/s
u2 = 1,6 m/s

Lưu ý quan trọng khi giải bài tập

Cần phân biệt rõ chiều dương và chiều âm khi giải bài tập. Chiều dương thường được chọn theo chiều chuyển động của vật có khối lượng lớn hơn.

Kiểm tra kết quả bằng cách tính động năng trước và sau va chạm. Động năng sau va chạm luôn nhỏ hơn động năng trước va chạm.

Với k = 1, va chạm là đàn hồi hoàn toàn. Với k = 0, va chạm là không đàn hồi. Các trường hợp còn lại là va chạm mềm một phần.

FAQ: Câu hỏi thường gặp về va chạm mềm

Trong quá trình giảng dạy, tôi nhận được rất nhiều câu hỏi từ học sinh về công thức va chạm mềm. Sau đây là những giải đáp cho các thắc mắc phổ biến nhất.

Sự khác biệt giữa va chạm mềm và va chạm cứng

Va chạm mềm xảy ra khi động năng của hệ không được bảo toàn hoàn toàn. Một phần động năng chuyển thành nhiệt năng và biến dạng.

Va chạm cứng ngược lại, động năng được bảo toàn hoàn toàn. Không có sự mất mát năng lượng trong quá trình va chạm.

Ví dụ điển hình là khi hai viên bi sắt va chạm (va chạm cứng) và hai viên đất sét va chạm (va chạm mềm).

Ứng dụng của va chạm mềm trong thực tế

Trong công nghiệp ô tô, các kỹ sư thiết kế cấu trúc xe dựa trên nguyên lý va chạm mềm. Phần đầu xe được làm từ vật liệu dễ biến dạng.

Điều này giúp hấp thụ lực va chạm, bảo vệ khoang hành khách khi xảy ra tai nạn. Đây là ứng dụng quan trọng nhất của va chạm mềm.

Trong thể thao, các tấm đệm bảo hộ cũng được thiết kế dựa trên nguyên lý này. Chúng giúp giảm thiểu chấn thương cho vận động viên.

Cách xác định hệ số phục hồi trong va chạm mềm

Hệ số phục hồi (k) được tính bằng tỉ số giữa vận tốc tương đối sau va chạm và vận tốc tương đối trước va chạm:

k = |(v2′

• v1′)| / |(v2 - v1)|

Trong đó:

• v1, v2: vận tốc các vật trước va chạm
• v1′, v2′: vận tốc các vật sau va chạm

Giá trị k luôn nằm trong khoảng từ 0 đến 1. Với va chạm mềm hoàn toàn, k = 0. Với va chạm đàn hồi hoàn toàn, k = 1.

Việc áp dụng công thức va chạm mềm đóng vai trò quan trọng trong nghiên cứu chuyển động của vật. Các định luật bảo toàn động lượng và cơ năng giúp giải thích chính xác quá trình va chạm giữa các vật. Thông qua hệ số phục hồi, ta có thể xác định mức độ mất mát năng lượng trong va chạm. Kiến thức này có nhiều ứng dụng thực tiễn trong kỹ thuật và đời sống hàng ngày.