Học thuộc công thức tính momen quán tính và các dạng bài tập cơ bản

Công thức tính momen quán tính giúp xác định khả năng chống lại sự thay đổi chuyển động quay của vật. Các công thức này phụ thuộc vào hình dạng, khối lượng và phân bố khối lượng của vật. Bài viết trình bày chi tiết các công thức cho thanh, đĩa, vòng tròn, hình trụ và quả cầu.

Công thức tính momen quán tính của vật rắn

Momen quán tính là đại lượng đặc trưng cho sự phân bố khối lượng của vật rắn đối với trục quay. Đây là khái niệm quan trọng trong cơ học.

Công thức tính momen quán tính của vật rắn được biểu diễn như sau:

I = ∑mi.ri²

Trong đó:

• I là momen quán tính (kg.m²)
• mi là khối lượng của phần tử thứ i (kg)
• ri là khoảng cách từ phần tử thứ i đến trục quay (m)

Với kinh nghiệm 20 năm giảng dạy, tôi thường ví von momen quán tính giống như “sức ì” của vật khi quay. Càng xa trục quay, momen quán tính càng lớn.

Ví dụ thực tế: Khi vận động viên trượt băng nghệ thuật muốn quay nhanh hơn, họ sẽ khép tay sát người. Điều này làm giảm khoảng cách r, từ đó giảm momen quán tính I.

Một số lưu ý khi tính momen quán tính:

• Đơn vị đo phải thống nhất trong hệ SI
• Với vật rắn đồng chất, có thể sử dụng tích phân thay cho tổng
• Momen quán tính phụ thuộc vào vị trí trục quay
• Giá trị momen quán tính luôn dương

Áp dụng công thức này giúp giải quyết nhiều bài toán về chuyển động quay trong vật lý. Đặc biệt quan trọng khi tính động năng quay và moment động lượng.

Khái niệm và ý nghĩa vật lý của momen quán tính

Momen quán tính đóng vai trò quan trọng trong việc mô tả chuyển động quay của vật thể. Nó thể hiện mức độ khó khăn khi làm thay đổi trạng thái chuyển động quay của vật.

Tương tự như khối lượng trong chuyển động tịnh tiến, momen quán tính là đại lượng đặc trưng cho quán tính của vật trong chuyển động quay. Giá trị của nó phụ thuộc vào phân bố khối lượng của vật so với trục quay.

Khi nghiên cứu về momen quán tính, chúng ta cần hiểu mối liên hệ với công thức tính momen ngẫu lực để có cái nhìn tổng quát về chuyển động quay.

Momen quán tính là gì và vai trò trong chuyển động quay

Momen quán tính được định nghĩa là tổng các tích của khối lượng các phần tử với bình phương khoảng cách từ phần tử đó đến trục quay. Công thức tổng quát:

I = Σ(mi.ri²)

Trong đó:

• I là momen quán tính
• mi là khối lượng phần tử thứ i
• ri là khoảng cách từ phần tử i đến trục quay

Momen quán tính có vai trò quyết định đến khả năng thay đổi trạng thái chuyển động quay. Vật có momen quán tính càng lớn càng khó thay đổi vận tốc góc.

Các yếu tố ảnh hưởng đến momen quán tính

Khối lượng và kích thước của vật là hai yếu tố chính ảnh hưởng đến momen quán tính. Với cùng một hình dạng, vật có khối lượng lớn hơn sẽ có momen quán tính lớn hơn.

Vị trí của trục quay cũng đóng vai trò quan trọng. Khi trục quay càng xa tâm khối lượng, momen quán tính càng lớn theo định lý trục song song Steiner.

Hình dạng và cách phân bố khối lượng của vật quyết định giá trị momen quán tính. Ví dụ: một thanh đồng chất quay quanh trục vuông góc với thanh có momen quán tính khác với khi quay quanh trục dọc theo thanh.

Đơn vị đo momen quán tính trong hệ SI

Trong hệ đơn vị SI, momen quán tính được đo bằng kg.m². Đây là đơn vị tổng hợp từ:

• Kilogram (kg): đơn vị khối lượng
• Mét vuông (m²): đơn vị khoảng cách bình phương

Việc hiểu rõ đơn vị đo giúp kiểm tra tính đúng đắn của kết quả tính toán. Trong thực tế, momen quán tính của vật thể thường có giá trị từ 10⁻⁶ đến 10⁶ kg.m².

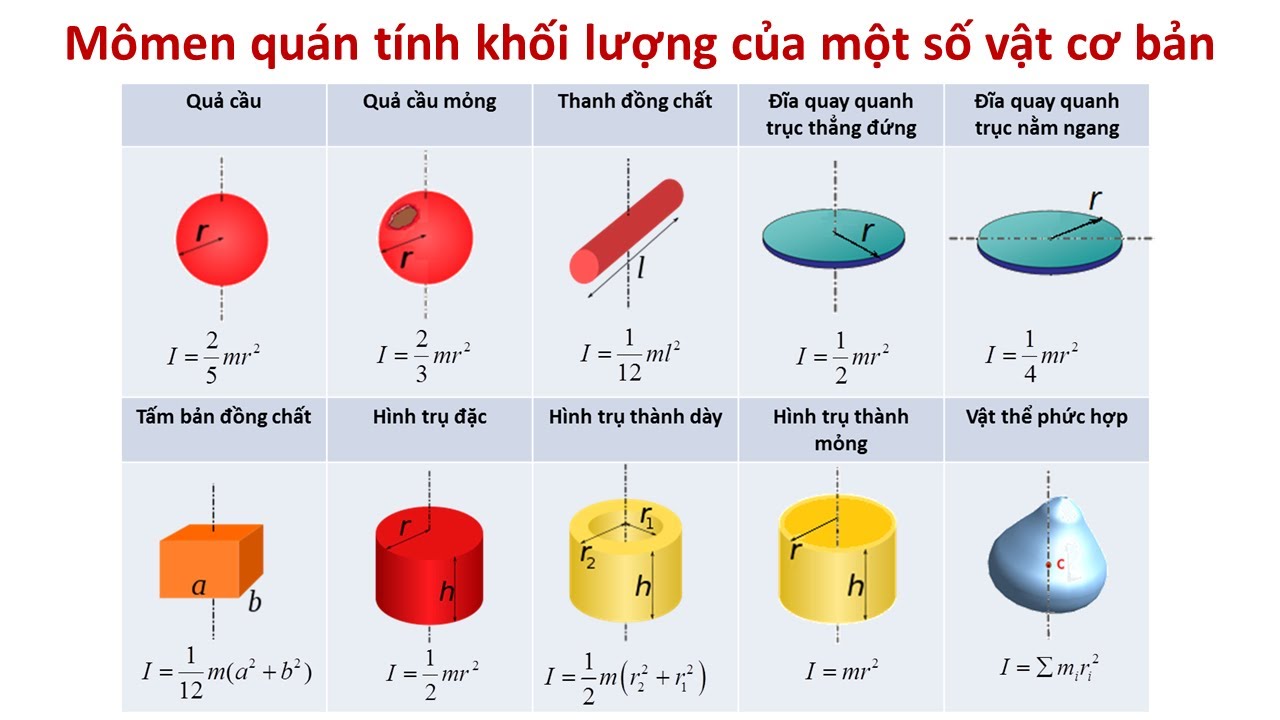
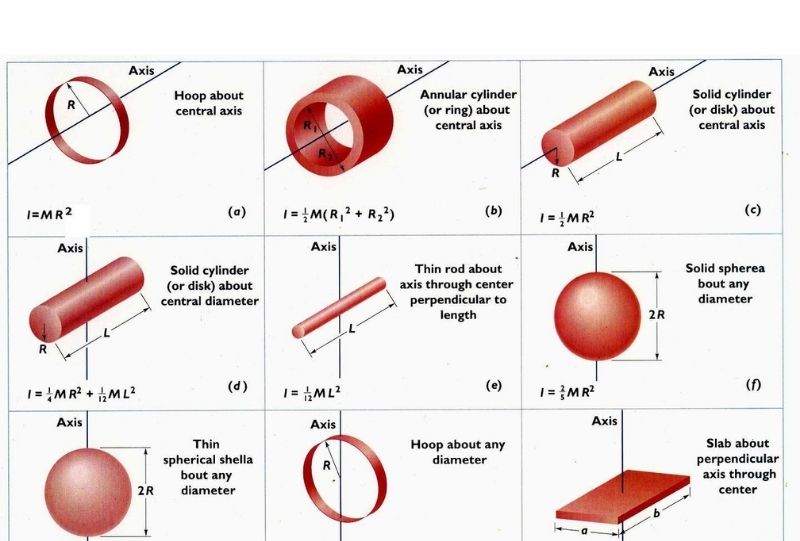
Công thức tính momen quán tính cho các vật thể cơ bản

Momen quán tính là đại lượng đặc trưng cho sự phân bố khối lượng của vật rắn quay quanh một trục. Công thức tính momen quán tính phụ thuộc vào hình dạng và kích thước của vật thể.

Để hiểu rõ hơn về momen quán tính, chúng ta cần nắm vững định luật hooke là gì và các công thức cơ bản cho từng dạng vật thể.

Momen quán tính của thanh đồng chất

Momen quán tính của thanh đồng chất quay quanh trục vuông góc với thanh và đi qua một đầu thanh được tính theo công thức:

I = (1/3)ML²

Trong đó:

• M là khối lượng của thanh
• L là chiều dài của thanh

Khi trục quay đi qua tâm thanh, momen quán tính sẽ là:

I = (1/12)ML²

Momen quán tính của đĩa tròn đồng chất

Momen quán tính của đĩa tròn đồng chất quay quanh trục vuông góc với mặt đĩa và đi qua tâm được xác định bởi:

I = (1/2)MR²

Trong đó:

• M là khối lượng của đĩa
• R là bán kính của đĩa

Công thức này thường được áp dụng cho các bánh đà trong máy móc và các thiết bị quay.

Momen quán tính của vòng tròn đồng chất

Momen quán tính của vòng tròn đồng chất quay quanh trục vuông góc với mặt vòng và đi qua tâm có dạng:

I = MR²

Với M là khối lượng và R là bán kính của vòng tròn. Công thức này đơn giản hơn so với đĩa tròn vì khối lượng tập trung ở chu vi.

Momen quán tính của hình trụ đặc

Momen quán tính của hình trụ đặc quay quanh trục đối xứng được tính theo công thức:

I = (1/2)MR²

Trong đó:

• M là khối lượng của hình trụ
• R là bán kính đáy hình trụ

Khi trục quay vuông góc với trục đối xứng và đi qua tâm khối, công thức sẽ là:

I = (1/4)MR² + (1/12)ML²

Momen quán tính của quả cầu đặc

Momen quán tính của quả cầu đặc quay quanh đường kính được xác định bởi:

I = (2/5)MR²

Trong đó:

• M là khối lượng của quả cầu
• R là bán kính của quả cầu

Công thức này không phụ thuộc vào trục quay đi qua tâm, do tính đối xứng của hình cầu.

Phương pháp giải bài tập momen quán tính

Momen quán tính là đại lượng đặc trưng cho sự phân bố khối lượng của vật rắn quay quanh một trục. Việc nắm vững cách giải bài tập momen quán tính giúp học sinh dễ dàng tiếp cận các bài toán phức tạp hơn.

Khi giải các bài tập về momen quán tính, việc áp dụng công thức chu kì con lắc đơn và công thức lực tương tác tĩnh điện thường xuyên xuất hiện trong các bài toán tổng hợp.

Các dạng bài tập thường gặp

Dạng 1: Tính momen quán tính của vật rắn đối với trục quay cố định. Đây là dạng bài cơ bản nhất, yêu cầu xác định I = Σmr².

Dạng 2: Tính momen quán tính của vật rắn đối với trục song song với trục đi qua khối tâm. Áp dụng định lý Steiner I = I₀ + md².

Dạng 3: Bài toán về động năng quay của vật rắn, sử dụng công thức Wđ = ½Iω². Loại bài này thường kết hợp với các định luật bảo toàn.

Phương pháp giải và mẹo làm bài

Bước 1: Xác định rõ dạng bài tập và các yếu tố đã cho trong đề bài. Vẽ hình minh họa nếu cần thiết.

Bước 2: Chọn hệ trục tọa độ phù hợp, xác định vị trí trục quay và khoảng cách từ các phần tử khối lượng đến trục.

Bước 3: Áp dụng công thức phù hợp với từng dạng bài. Với vật có hình dạng đặc biệt, sử dụng các công thức có sẵn.

Kinh nghiệm giảng dạy cho thấy học sinh thường mắc lỗi khi xác định khoảng cách r. Cần đặc biệt lưu ý r là khoảng cách vuông góc từ phần tử khối lượng đến trục quay.

Bài tập mẫu có lời giải chi tiết

Bài toán: Tính momen quán tính của một thanh đồng chất, chiều dài L = 1m, khối lượng M = 2kg đối với trục vuông góc với thanh và đi qua một đầu thanh.

Lời giải:

• Bước 1: Chia thanh thành các phần tử vi phân dx
• Bước 2: Khối lượng phần tử dm = (M/L)dx
• Bước 3: Momen quán tính của phần tử dI = x²dm
• Bước 4: Tích phân I = ∫(0→L) x²(M/L)dx = ML²/3 = 2/3 (kg.m²)

Qua ví dụ trên, ta thấy việc chia nhỏ vật thành các phần tử vi phân và tích phân là phương pháp hiệu quả để giải các bài toán phức tạp.

FAQ: Câu hỏi thường gặp về momen quán tính

Momen quán tính là một khái niệm quan trọng trong vật lý. Tôi sẽ giải đáp các thắc mắc phổ biến về đại lượng này.

Mối quan hệ giữa momen quán tính và động năng quay

Momen quán tính của vật rắn có mối liên hệ trực tiếp với động năng quay. Động năng quay được tính theo công thức:

Eđ = (1/2)Iω2

Trong đó:

• I là momen quán tính
• ω là vận tốc góc

Khi momen quán tính càng lớn, động năng quay càng tăng. Điều này giống như việc tính nồng độ phần trăm khi pha chế dung dịch vậy.

Cách xác định trục quay để tính momen quán tính

Việc xác định trục quay đúng rất quan trọng. Trục quay phải đi qua tâm khối của vật rắn đối xứng.

Với vật có hình dạng đều đặn như hình cầu, hình trụ, trục quay thường đi qua tâm đối xứng.

Đối với vật không đối xứng, cần xác định trọng tâm và cho trục quay đi qua đó để có kết quả chính xác.

Ứng dụng của momen quán tính trong thực tế

Momen quán tính được ứng dụng rộng rãi trong công nghiệp và đời sống. Bánh đà trong động cơ xe máy là ví dụ điển hình.

Các vận động viên trượt băng nghệ thuật cũng vận dụng nguyên lý này. Khi họ khép tay vào người, momen quán tính giảm giúp tăng tốc độ quay.

Trong thiết kế máy móc, hiểu về momen quán tính giúp tối ưu hiệu suất và độ bền của các chi tiết quay.

Việc áp dụng công thức tính momen quán tính đúng cách giúp giải quyết nhiều bài toán về chuyển động quay. Các công thức tính momen quán tính của thanh, đĩa, vòng tròn, hình trụ và quả cầu đã được trình bày chi tiết kèm ví dụ minh họa. Kiến thức này có ý nghĩa quan trọng trong việc tính toán và thiết kế các hệ thống cơ khí thực tế.