Học công thức tính momen ngẫu lực và ứng dụng trong chuyển động quay

Công thức tính momen ngẫu lực là kiến thức quan trọng trong chương trình vật lý. Momen ngẫu lực xuất hiện trong nhiều hiện tượng cơ học. Các ứng dụng thực tế của nó có trong máy móc và thiết bị kỹ thuật. Bài viết trình bày chi tiết cách tính toán và giải bài tập về momen ngẫu lực.

Công thức tính momen ngẫu lực

Momen ngẫu lực là đại lượng đặc trưng cho tác dụng quay của một ngẫu lực. Để tính được momen ngẫu lực, ta cần nắm rõ công thức tính momen ngẫu lực cơ bản.

Công thức tổng quát:

M = F × d

Trong đó:

• M: Momen ngẫu lực (đơn vị N.m)
• F: Độ lớn của lực (đơn vị N)
• d: Khoảng cách giữa hai lực song song ngược chiều (đơn vị m)

Khi áp dụng công thức, cần lưu ý chiều của momen ngẫu lực. Nếu ngẫu lực tạo ra chuyển động quay ngược chiều kim đồng hồ, momen dương. Ngược lại, momen âm khi chuyển động cùng chiều kim đồng hồ.

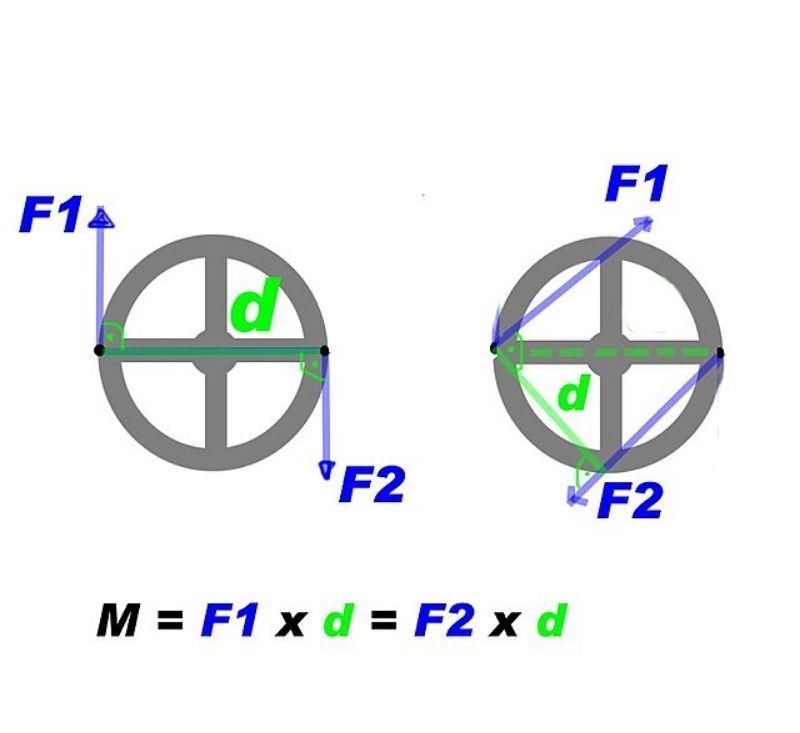
Ví dụ thực tế: Khi mở nắp chai nước, tay ta tạo ra một ngẫu lực. Lực F tác dụng lên nắp chai và khoảng cách d từ tâm nắp đến điểm đặt lực tạo thành momen ngẫu lực giúp xoay nắp chai.

Một kinh nghiệm giảng dạy của tôi là luôn yêu cầu học sinh vẽ hình minh họa trước khi tính toán. Điều này giúp xác định chính xác chiều của momen và tránh nhầm lẫn khi áp dụng công thức.

Khái niệm và đặc điểm của momen ngẫu lực trong vật lý

Momen ngẫu lực là một khái niệm quan trọng trong cơ học, đặc biệt khi nghiên cứu chuyển động quay của vật thể. Để hiểu rõ hơn về công thức momen ngẫu lực, ta cần nắm vững các thành phần cơ bản và đặc điểm của nó.

Định nghĩa momen ngẫu lực

Momen ngẫu lực là đại lượng đặc trưng cho tác dụng quay của một cặp lực có độ lớn bằng nhau, cùng phương, ngược chiều và không cùng nằm trên một đường thẳng. Giá trị của momen ngẫu lực được tính bằng tích của một lực trong cặp với khoảng cách giữa hai lực.

Trong quá trình giảng dạy, tôi thường lấy ví dụ về việc vặn một cái vít

• khi ta tác dụng lực vào cờ lê, càng xa điểm tác dụng thì càng dễ vặn. Điều này minh họa rất rõ vai trò của khoảng cách trong momen ngẫu lực.

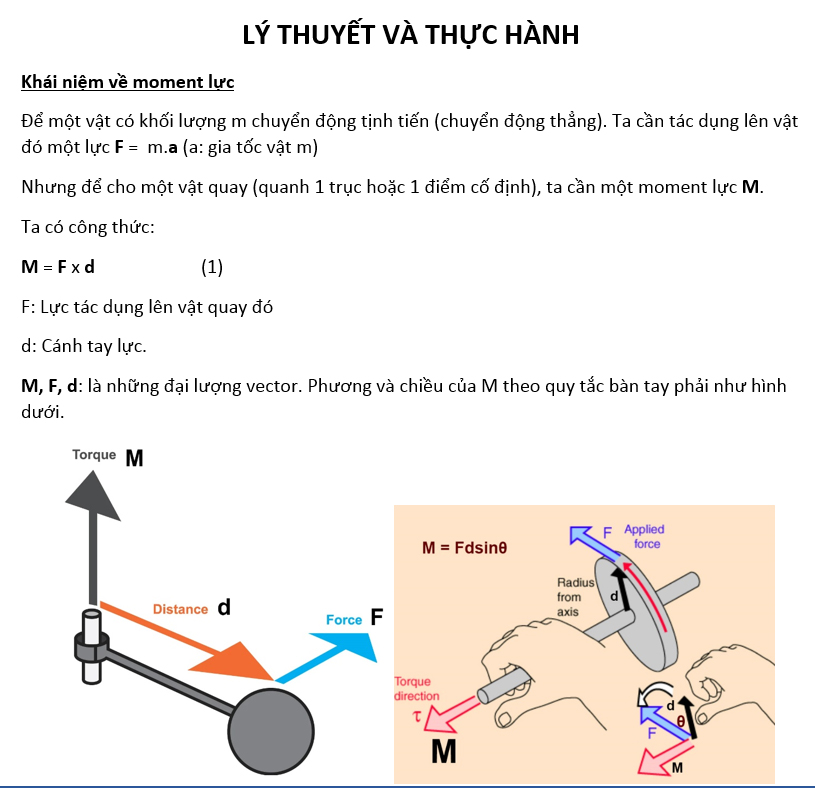
Đặc điểm và tính chất của ngẫu lực

Ngẫu lực có những đặc điểm độc đáo giúp phân biệt với các loại lực khác. Momen ngẫu lực không phụ thuộc vào vị trí điểm đặt của hệ quy chiếu, mà chỉ phụ thuộc vào độ lớn của lực và khoảng cách giữa hai lực.

Kinh nghiệm giảng dạy cho thấy học sinh thường nhầm lẫn giữa momen ngẫu lực và công thức tính momen quán tính. Hai khái niệm này hoàn toàn khác nhau về bản chất và cách áp dụng.

Vai trò của momen ngẫu lực trong chuyển động quay

Momen ngẫu lực đóng vai trò quyết định trong việc tạo ra chuyển động quay của vật. Nó là nguyên nhân làm thay đổi trạng thái chuyển động quay của vật, tương tự như lực trong chuyển động tịnh tiến.

Trong thực tế, momen ngẫu lực được ứng dụng rộng rãi trong các máy móc và thiết bị cơ khí. Ví dụ như trong động cơ ô tô, momen xoắn từ động cơ được truyền qua hệ thống truyền động để tạo ra chuyển động quay của bánh xe.

Cách tính momen ngẫu lực và các trường hợp áp dụng

Momen ngẫu lực là đại lượng đặc trưng cho tác dụng quay của ngẫu lực. Việc tính toán công thức tính momen ngẫu lực đóng vai trò quan trọng trong nhiều bài toán cơ học.

Khi giảng dạy về momen ngẫu lực, tôi thường liên hệ với việc vặn ốc vít. Lực càng vuông góc với cờ lê, momen càng lớn và việc vặn càng dễ dàng.

Công thức tổng quát tính momen ngẫu lực

Công thức tổng quát:

M = F × d

Trong đó:

• M là momen ngẫu lực (N.m)
• F là độ lớn của lực (N)
• d là khoảng cách giữa hai lực song song ngược chiều (m)

Tương tự như công thức tính thời gian rơi, công thức này cũng cần chú ý đơn vị đo.

Các trường hợp đặc biệt khi tính momen ngẫu lực

Trường hợp lực không vuông góc với cánh tay đòn:

M = F × d × sinα

α là góc giữa vector lực và cánh tay đòn.

Khi tính công thức tính công của lực lạ, ta cũng cần quan tâm đến góc α tương tự.

Trường hợp nhiều ngẫu lực tác dụng:

M = M1 + M2 + … + Mn

Momen tổng hợp bằng tổng đại số các momen thành phần.

Ví dụ minh họa và bài tập áp dụng

Bài tập 1: Tính momen ngẫu lực khi F = 10N, d = 0,5m
Giải:
M = F × d = 10 × 0,5 = 5 N.m

Bài tập 2: Tính momen khi F = 20N, d = 0,3m, α = 60°
Giải:
M = F × d × sin60° = 20 × 0,3 × 0,866 = 5,196 N.m

Kinh nghiệm giải nhanh: Vẽ hình minh họa sẽ giúp xác định chính xác góc α và cánh tay đòn d.

Ứng dụng của momen ngẫu lực trong thực tế

Momen ngẫu lực đóng vai trò quan trọng trong nhiều lĩnh vực kỹ thuật và đời sống. Công thức tính momen ngẫu lực M = F × r giúp ta hiểu rõ hơn về mối quan hệ giữa lực và khoảng cách.

Việc áp dụng momen ngẫu lực đúng cách sẽ tối ưu hóa hiệu quả công việc. Tôi thường lấy ví dụ về cánh tay đòn khi giảng dạy để học sinh dễ hình dung.

Ứng dụng trong máy móc và thiết bị

Trong động cơ ô tô, momen xoắn quyết định khả năng tăng tốc của xe. Lực từ pittông được truyền qua trục khuỷu tạo momen quay.

Các thiết bị nâng như cần cẩu sử dụng nguyên lý momen để nâng vật nặng. Khoảng cách từ điểm tựa đến vật càng xa, momen càng lớn.

Tôi từng hướng dẫn sinh viên thiết kế hệ thống bánh răng cho máy công nghiệp. Việc tính toán momen chính xác giúp máy hoạt động ổn định và bền bỉ.

Ứng dụng trong các bài toán kỹ thuật

Khi thiết kế cầu, kỹ sư phải tính toán momen uốn tác động lên các dầm. Điều này liên quan đến công thức tính năng lượng của con lắc lò xo.

Trong xây dựng, momen xoắn ảnh hưởng đến độ bền của cột và dầm. Kinh nghiệm cho thấy cần tăng cường cốt thép ở vị trí chịu momen lớn.

Các bài toán về công thức thế năng con lắc đơn thường xuất hiện khi phân tích dao động của kết cấu.

Mối liên hệ với các đại lượng vật lý khác

Momen ngẫu lực có mối quan hệ mật thiết với động năng quay. Khi momen tăng, vận tốc góc của vật cũng tăng theo.

Trong chuyển động quay, momen quán tính phụ thuộc vào phân bố khối lượng. Điều này ảnh hưởng trực tiếp đến momen ngẫu lực cần tạo ra.

Công suất trong chuyển động quay được tính bằng tích của momen và vận tốc góc. Đây là cơ sở để tính hiệu suất của máy móc.

FAQ: Câu hỏi thường gặp về momen ngẫu lực

Các câu hỏi thường gặp về momen ngẫu lực giúp học sinh hiểu rõ hơn về khái niệm quan trọng này trong vật lý. Tôi sẽ giải đáp chi tiết từng vấn đề mà các em hay thắc mắc.

Sự khác biệt giữa momen lực và momen ngẫu lực

Momen lực và momen ngẫu lực có sự khác biệt cơ bản về bản chất và tác dụng. Momen lực là tác dụng của một lực đơn lẻ gây ra chuyển động quay quanh một trục.

Trong khi đó, momen ngẫu lực là tác dụng của một cặp lực song song, ngược chiều và có độ lớn bằng nhau. Điều này tương tự như tác dụng của lực kéo về công thức trong dao động điều hòa.

Cách xác định chiều của momen ngẫu lực

Để xác định chiều của momen ngẫu lực, ta áp dụng quy tắc nắm tay phải. Ngón cái chỉ theo chiều của momen ngẫu lực, các ngón còn lại cuộn theo chiều quay.

Cách này giúp học sinh dễ nhớ và áp dụng, tương tự như xác định chiều dao động của Công thức con lắc đơn. Tôi thường hướng dẫn học sinh thực hành trực tiếp với bút chì để hiểu rõ hơn.

Mối quan hệ giữa momen ngẫu lực và chuyển động quay

Momen ngẫu lực tạo ra chuyển động quay thuần túy của vật. Khi momen ngẫu lực tác dụng, vật sẽ quay quanh trục đi qua trọng tâm.

Giá trị của momen ngẫu lực không phụ thuộc vào vị trí điểm đặt. Điều này khác với momen lực thông thường phụ thuộc vào khoảng cách từ điểm đặt đến trục quay.

Trong thực tế, momen ngẫu lực xuất hiện khi ta vặn một con ốc bằng cờ lê hoặc xoay nắp chai. Hiểu được nguyên lý này giúp ta thao tác hiệu quả hơn.

Việc áp dụng công thức tính momen ngẫu lực đóng vai trò quan trọng trong nghiên cứu chuyển động quay của vật thể. Các công thức tính toán đơn giản cùng với những ví dụ minh họa cụ thể giúp người học dễ dàng nắm bắt và vận dụng kiến thức vào thực tế. Momen ngẫu lực xuất hiện phổ biến trong các thiết bị máy móc và có mối liên hệ mật thiết với nhiều đại lượng vật lý khác trong chuyển động quay.