Công thức tính gia tốc rơi tự do và bài tập điển hình 

Công thức tính gia tốc rơi tự do là kiến thức quan trọng với môn Vật lý. Học sinh muốn giải bài tập và vượt qua các kì thi cần hiểu rõ khái niệm, cách tính cho từng dạng bài tập.

Gia tốc rơi tự do là gì?

Gia tốc rơi tự do là gia tốc của vật khi chuyển động rơi tự do. Đại lượng này ký hiệu là g, đơn vị tính m/s^2, còn gọi là gia tốc trọng tường hay gia tốc của trường trọng lực.

Tại một nơi nhất định trên Trái đất và gần mặt đất, các vật đều rơi tự do cùng một gia tốc. Tại những vĩ độ khác nhau, gia tốc thường là khoảng 9.8 m/s^2 hoặc 10 m/s^2..

Các vật rơi trong không khí nhanh hay chậm còn do lực cản của không khí tác động khác nhau. Rơi tự do trong chân không đã loại bỏ ảnh hưởng của không khí nên các vật rơi nhanh như nhau (Đây chính là hiện tượng rơi tự do).

Nghiên cứu đo lường giá trị của gia tốc trọng trường:

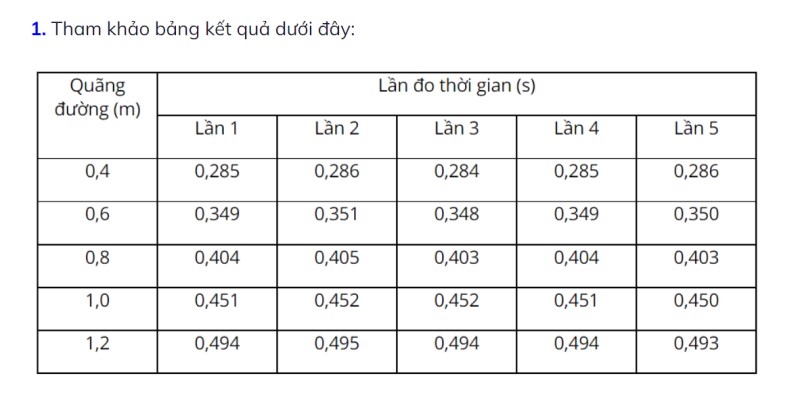
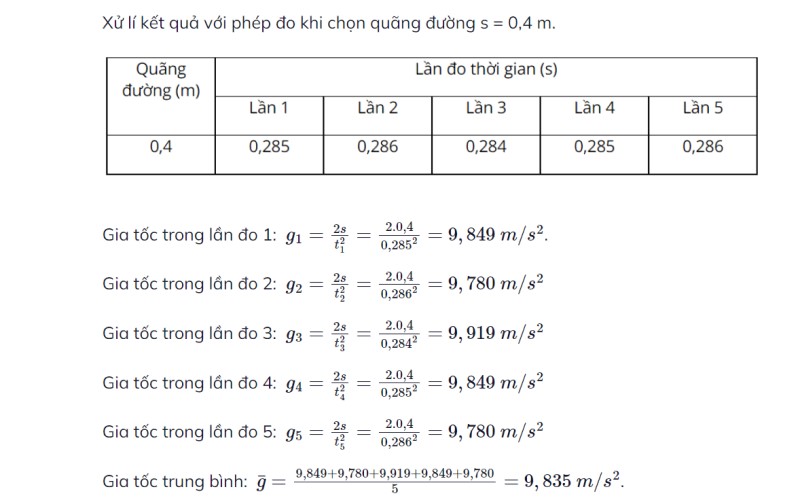
Tính chất của hiện tượng rơi tự do

Phương của sự rơi tự do thẳng đứng, giống với phương của dây rọi, chiều chuyển động từ trên hướng xuống. Lưu ý, tính chất của chuyển động này thẳng nhanh dần đều.

Các bài tập về công thức tính gia tốc rơi tự do

Các bài toán liên quan đến gia tốc rơi tự do được ứng dụng rất phổ biến. Một số bài toán được đưa ra đều có cách giải chi tiết, học sinh có thể tham khảo để chuẩn bị cho những kỳ thi sắp tới.

1. Tìm gia tốc tự do tại một nơi có độ cao bằng nửa bán kính trái đất. Biết giá trị gia tốc trọng trường là g = 10m/s^2.

Gia tốc khi vật ở mặt đất là: g = GM/R^2 = 10m/s^2 => g(h) = GM/(R+H)^2 = 40/(3/2 x R)^2 = 40/9 (m/s^2).

2. Biết gia tốc rơi tự do trên bề mặt của mặt trăng là 1.6m/s^2, R(MT) = 1740 km. Vậy g = 1/9g(MT) khi ở độ cao nào so với mặt trăng?

Gia tốc ở mặt trăng g(T) = GM(T)/R(T)^2

Gia tốc ở độ cao h: g(h) = GM(T)/(R(T) + h)^2 => g(T)/g(h) = [R(T) +h]^2/R(T)^2 = 9. Vậy h = 3480km.

Giải bài tập liên quan sự rơi tự do

Có nhiều dạng bài tập liên quan đến sự rơi tự do. Tùy từng đặc điểm các dạng khác nhau, bạn có thể tìm ra cách giải cho bài toán mình gặp phải.

Dạng 1: Bài toán tính quãng đường, vận tốc và thời gian

Đối với bài này, bạn cần dùng công thức gồm:

• Tính quãng đường: S = h = 1/2 x g x (t^2).
• Công thức vận tốc: v = g x t.

Đề vài mẫu số 1: Một vật được thả rơi tự do khi chạm đất có v = 20m/s. Xác định độ cao vật được thả rơi, với g = 10m/s^2.

Đối với đề bài này, bạn xác định thời gian từ công thức v = v0 + gt => t = v/g = 2s.

Độ cao vật được thả rơi là h = S = 1/2 x g x (t^2) = 1/2 x 10 x (2^2) = 20m.

Đề bài mẫu số 2: Cho độ cao 100m, người ta bắt đầu thả vật chiều thẳng đứng với v = 10m/s, g = 10m/s^2.

1. Xác định sau bao lâu vật này sẽ chạm chất?
2. Tính vận tốc của vật lúc vừa chạm đất

Giải bài:

6. S = v0 x t + 1/2 x g x (t^2) => 100 = 10t + 5(t^2) => t = 6.2s hoặc -16.2s.

Thời gian chỉ nhận giá trị riêng nên chọn đáp án 6.2s.

6. Vận tốc khi vật chạm đất là: v = v0 + gt = 10 + 10 x 6.2 = 72m/s.

Dạng 2: Tìm quãng đường được đi trong khoảng thời gian n giây

Quãng đường vật đi trong giây thứ n, công thức tính gồm:

• Quãng đường vật đi trong n giây: S1 = 1/2 x g x (n^2).
• Quãng đường đi trong (n-1) giây: S2 = 1/2 x g x (n-1)^2.

=> Quãng đường vật đi trong giây thứ n là dS = S1

• S2.

• S2.

Đề bài gợi ý: Vật rơi tự do tại vị trí có g = 10 m/s^2, làm theo các yêu cầu:

1. Quãng đường đi trong 5s đầu tiên.
2. Quãng đường vật đi trong giây thứ 4 và giây thứ 5.

Giải bài:

1. Quãng đường vật đi trong 5s đầu: S5 = 1/2 x g x (t5)^2 = 1/2 x 10 x 5^2 = 125m.
2. Quãng đường vật đi trong 4s đầu là: S4 = 1/2 x g x (t4)^2 = 1/2 x 10 x 4^2 = 80m.

Quãng đường vật đó đã đi trong giây thứ 5 là: S5

• S4 = 125 - 80 = 45m.

Quãng đường vật đi trong 3s đầu là: S3 = 1/2 x g x (t3)^2 = 1/2 x 10 x 3^2 =45m.

Quãng đường vật đi trong giây thứ 4 là: S4

• S3 = 80 - 45 = 35m.

Dạng 3: Tính quãng đường đi được trong n giây cuối

Dạng bài này yêu cầu xác định quãng đường vật đi trong n giây cuối. Cách tính áp dụng lần lượt theo các bước:

• Bước 1: Xác định quãng đường đi trong t giây: S1 = 1/2 x g x (t^2).
• Bước 2: Tính quãng đường đi trong (t
  • n) giây: S2 = 1/2 x g x (t - n)^2.

=> Quãng đường đi trong n giây cuối là: dS = S1  - S2.

Đề bài minh họa: Vật rơi tự do không vận tốc đầu với độ cao 80m xuống mặt đất. Tính quãng đường vật rơi trong 0.5 giây cuối cùng, biết g = 10m/s^2.

Ta có: S = 1/2 x g x (t^2) => 80 = 1/2 x 10 x (t^2) => t = 4s.

Quãng đường vật đi trong 3.5s đầu là: S1 = 1/2 x g x (t^2) = 1/2 x 10 x (3.5)^2 = 61.25m.

Quãng đường vật rơi trong 0.5s cuối là: dS = S

• S1 = 80 - 61.25 = 18.75m.

Kết luận

Xác định công thức tính gia tốc rơi tự do và những yếu tố liên quan đều căn cứ vào công thức. Để có được kết quả tốt nhất trong các kỳ thì, bạn nên luyện các bài tập mẫu để giải bài chuẩn hơn.