Công thức tính độ dịch chuyển chi tiết | Lý thuyết độ dịch chuyển

Công thức tính độ dịch chuyển cho biết khoảng cách của vật khi thay đổi vị trí. Khái niệm này khác với quãng đường và có vai trò quan trọng trong quá trình xác định vận tốc, thời gian nên bạn cần ghi nhớ kỹ.

Công thức tính độ dịch chuyển là gì và lý thuyết cụ thể

Công thức độ dịch chuyển xác định khoảng cách giữa hai vị trí đầu

• cuối của vật sau khi vật này thay đổi vị trí. Có thể hiểu đây là độ dài được đo từ vị trí ban đầu với vị trí hiện tại của vật.

Điều kiện để xác định được độ dịch chuyển là vật phải di chuyển (dời) theo một hướng xác định. Trên đồ thị, đại lượng này được biểu diễn bằng mũi tên nối vị trí đầu và cuối.

Thuật ngữ này khác với quãng đường di chuyển của vật nên bạn cần chú ý phân biệt. Nó là đại lượng vectơ, độ lớn tỉ lệ với độ dài, cho biết khoảng cách giữa hai điểm vị trí cũng như hướng dịch chuyển của vật.

Công thức xác định độ dịch chuyển của vật chính xác: Δx = x2 − x1.

Dựa trên đồ thị sẽ có phương trình như sau: d = v0.t + 1/2.a.t^2, trong đó v0 là vận tốc ban đầu, t là đại lượng thời gian và a biểu thị gia tốc vật.

Trong chuyển động thẳng đều, độ dịch chuyển sẽ bằng với quãng đường. Công thức tính lúc này là d = s = v.t với v là vận tốc còn t là thời gian di chuyển.

Lưu ý rằng khi vật chuyển động theo chiều dương nhưng sau đó đổi chiều thì lúc này vận tốc là một số âm nhưng tốc độ vẫn là một số dương.

Trường hợp vật di chuyển từ vị trí này đến vị trí kia bằng nhiều đoạn khác nhau thì phải áp dụng công thức tính độ dịch chuyển tổng hợp. Dạng chính của công thức này là phép cộng vectơ.

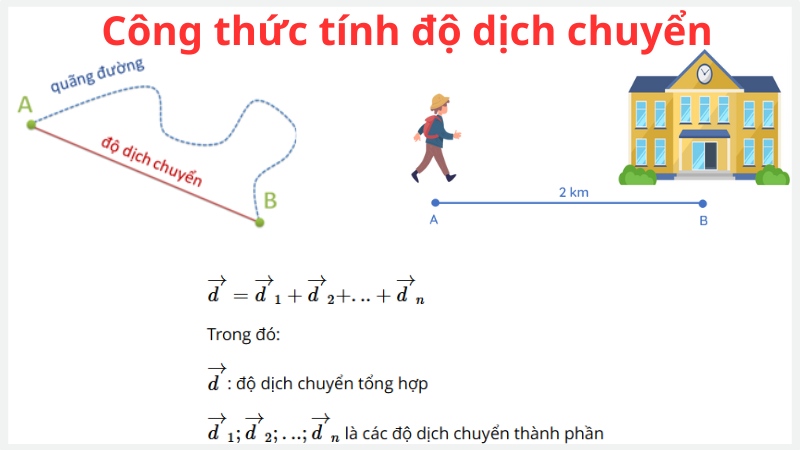
Đồ thị độ dịch chuyển của một vật

Đại lượng này có thể được biểu diễn thông qua đồ thị để xác định sự thay đổi vị trí. Thông qua việc vẽ đồ thị thời gian

• độ dịch chuyển có thể tính được vận tốc của một vật.

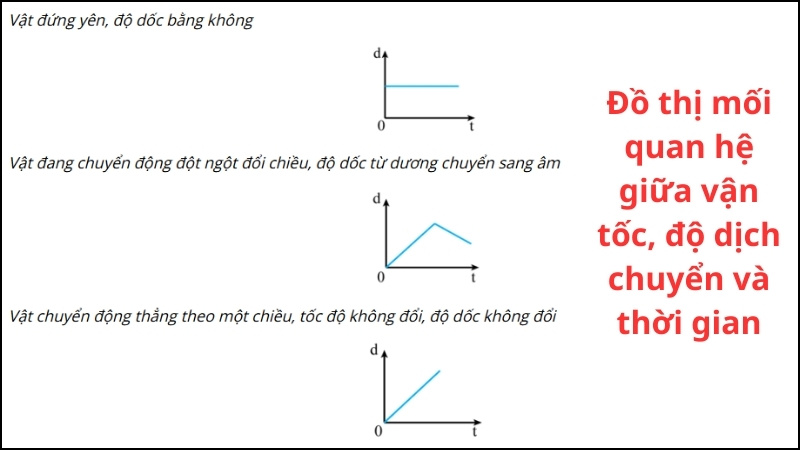
Cách này thường được thực hiện sau khi đã áp dụng công thức tính độ dịch chuyển để có kết quả d chính xác.

Để hoàn thành cần xác định các đại lượng và thực hiện vẽ lần lượt:

• Bước 1: Xây dựng hệ tọa độ với Ox
  • Oy, gốc là vị trí của vật mốc, thông thường trong thực tế trục hoành Ox  sẽ có hướng Tây Đông còn trục tung Oy có hướng Bắc Nam.
• Bước 2: Xác định mốc thời gian để tiến hành đi khoảng cách từ thời điểm bắt đầu cho đến thời điểm cần xác định để tính độ dịch chuyển.
• Bước 3: Nối vị trí đầu và cuối của chuyển động, lưu ý độ dài phải tỉ lệ với độ lớn của d.
• Bước 4: Xác định vận tốc dựa trên độ dốc của độ dịch chuyển, có thể là âm hoặc dương.

Để hiểu rõ hơn về đồ thị độ dịch chuyển và ứng dụng cụ thể bạn hãy xem ví dụ:

Phân biệt độ dịch chuyển và quãng đường đi được chi tiết

Như đã trình bày ở phần khái niệm, hai đại lượng này khác nhau về cả bản chất, cách tính. Điểm chung duy nhất là chúng phản ánh chuyển động của một vật, có sự thay đổi vị trí.

Quãng đường là đại lượng được sử dụng vô cùng phổ biến nhưng không phải lúc nào cũng đúng khi mô tả khoảng cách giữa hai vị trí của vật. Từ điểm bắt đầu, vật có thể di chuyển theo nhiều hướng để tới được điểm hiện tại.

Thế nên bản chất của quãng đường là đại lượng vô hướng. Nó phản ánh tổng khoảng cách mà vật đi được.

Độ dịch chuyển là một đại lượng có hướng, xét từ điểm ban đầu mà vật đứng. Cách tính là lấy vị trí cuối trừ vị trí đầu để ra khoảng cách với một hướng xác định.

Bài tập ứng dụng công thức tính độ dịch chuyển

Đề 1:

Đề 2:

Kết luận

Công thức tính độ dịch chuyển giúp bạn xác định hướng đi của vật và khoảng cách hai điểm đầu cuối. Đây là đại lượng cần thiết để tính được vận tốc cũng như thời gian di chuyển của vật.