Tìm hiểu công thức tính độ cao h và các ứng dụng trong thực tế

Công thức tính độ cao h là kiến thức quan trọng trong chương trình vật lý phổ thông. Độ cao h giúp xác định vị trí của vật trong không gian ba chiều. Các phương pháp tính toán độ cao h đều dựa trên nguyên lý hình học và lượng giác cơ bản.

Công thức tính độ cao h

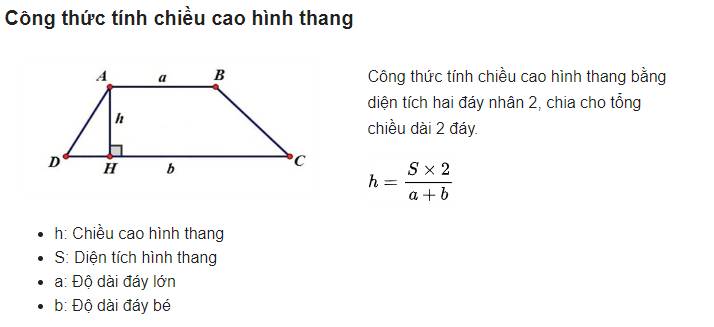
Độ cao h là khoảng cách từ chân đường vuông góc đến đỉnh của một hình. Để tính công thức tính độ cao h, ta cần dựa vào diện tích và cạnh đáy của hình.

Công thức tổng quát:

h = (2 × S) ÷ a

Trong đó:

• h: độ cao cần tính
• S: diện tích hình
• a: độ dài cạnh đáy

Ví dụ thực tế khi tôi giảng dạy cho học sinh lớp 8: Một tam giác có diện tích 24cm2, cạnh đáy 8cm. Áp dụng công thức trên:

h = (2 × 24) ÷ 8 = 6cm

Một số lưu ý quan trọng khi sử dụng công thức:

• Đơn vị của h và a phải thống nhất
• Với hình chữ nhật, h chính là chiều cao
• Với hình thang, h là khoảng cách giữa 2 đáy song song

Kinh nghiệm 20 năm giảng dạy cho thấy học sinh thường nhầm lẫn giữa chiều cao và cạnh xiên. Chiều cao luôn vuông góc với cạnh đáy và ngắn nhất so với các đường xiên.

Để kiểm tra kết quả tính h đúng hay sai, ta có thể thay ngược vào công thức tính diện tích S = (a × h) ÷ 2. Nếu ra đúng diện tích ban đầu thì kết quả chính xác.

Các thành phần và ý nghĩa trong công thức tính độ cao h

Trong vật lý, công thức tính độ cao h là một phương trình quan trọng để xác định khoảng cách theo chiều thẳng đứng từ một điểm đến mặt phẳng tham chiếu.

Công thức cơ bản được biểu diễn:

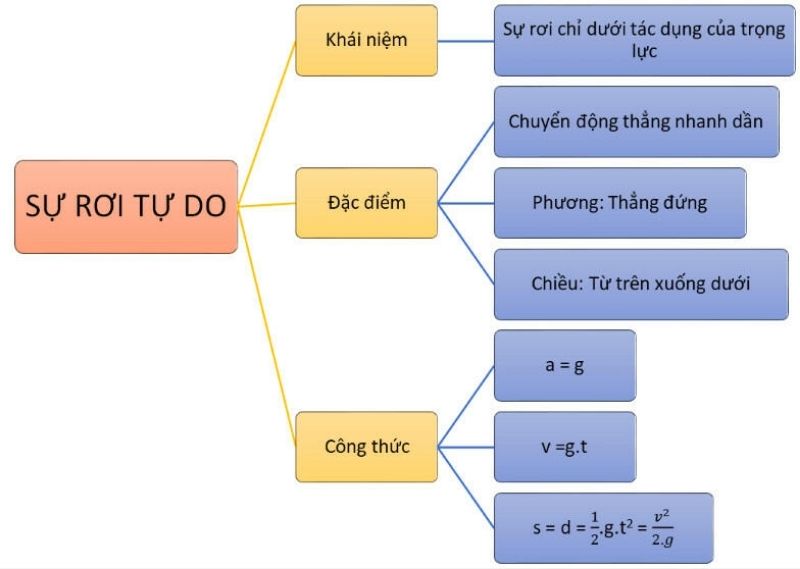
h = h0 + v0t + (1/2)gt²

Trong đó:

• h: độ cao tại thời điểm t
• h0: độ cao ban đầu
• v0: vận tốc ban đầu theo phương thẳng đứng
• g: gia tốc trọng trường
• t: thời gian chuyển động

Các đại lượng cơ bản trong công thức

Mỗi thành phần trong công thức đóng vai trò riêng biệt:

h0 thể hiện vị trí xuất phát của vật, có thể bằng 0 nếu vật xuất phát từ mặt đất.

v0t biểu thị quãng đường vật đi được nếu chỉ có vận tốc ban đầu, không chịu ảnh hưởng của trọng lực.

(1/2)gt² phản ánh ảnh hưởng của trọng lực lên chuyển động của vật theo thời gian.

Đơn vị đo độ cao h

Trong hệ SI, độ cao h được đo bằng mét (m). Tuy nhiên có thể quy đổi sang các đơn vị khác:

• mét = 100 centimét
• kilômét = 1000 mét

Khi giải bài tập, cần đặc biệt chú ý quy đổi các đơn vị về cùng hệ đo để tránh sai sót.

Ý nghĩa vật lý của độ cao h

Độ cao h cho biết vị trí của vật trong không gian theo phương thẳng đứng. Đây là đại lượng quan trọng trong:

Tính toán thế năng của vật:

E = mgh

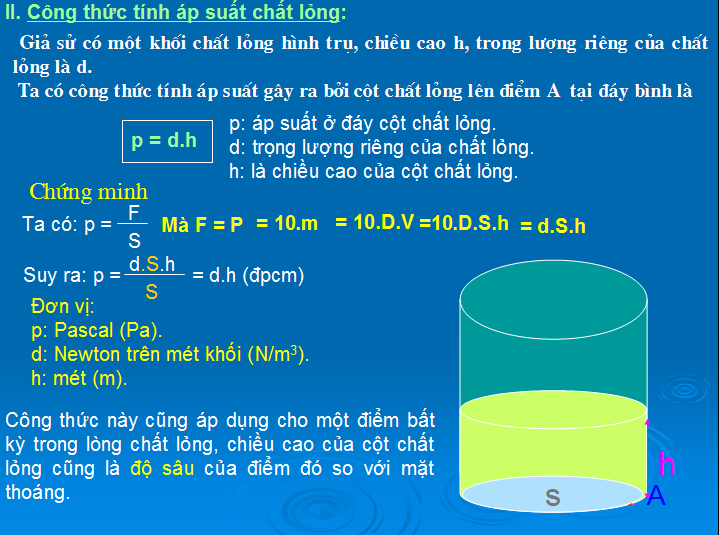
Xác định áp suất thủy tĩnh:

p = ρgh

Trong 20 năm giảng dạy, tôi thường nhắc học sinh rằng độ cao h giống như “thước đo” vị trí của vật so với mặt đất.

Cách áp dụng công thức tính độ cao h trong thực tế

Công thức tính độ cao h được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Từ xây dựng công trình đến thiết kế nội thất, việc tính toán chính xác độ cao là yếu tố then chốt.

Trong quá trình giảng dạy, tôi thường lấy ví dụ về việc tính độ cao của một tòa nhà. Học sinh sẽ dễ dàng hình dung và áp dụng công thức khi nhìn thấy các ví dụ thực tế.

Khi gặp lỗi Error: 529 trong quá trình tính toán, cần kiểm tra lại các thông số đầu vào. Đây là lỗi thường gặp do nhập sai dữ liệu hoặc đơn vị đo không đồng nhất.

Các bước tính độ cao h

Bước 1: Thu thập đầy đủ các thông số cần thiết như góc nghiêng, khoảng cách và các điều kiện ràng buộc.

Bước 2: Chuyển đổi các đơn vị đo về cùng một hệ thống để tránh sai số trong tính toán.

Bước 3: Áp dụng công thức và kiểm tra kết quả bằng phương pháp ước lượng sơ bộ.

Lưu ý khi sử dụng công thức

Kinh nghiệm cho thấy việc làm tròn số cần được thực hiện một cách hợp lý. Không nên làm tròn quá sớm trong quá trình tính toán.

Các đơn vị đo phải thống nhất từ đầu đến cuối. Đây là nguyên nhân phổ biến dẫn đến sai số trong kết quả cuối cùng.

Nên vẽ sơ đồ minh họa trước khi tính toán để hình dung rõ bài toán và tránh nhầm lẫn các thông số.

Sai số thường gặp và cách khắc phục

Sai số do dụng cụ đo đạc là vấn đề phổ biến nhất. Cần sử dụng thiết bị đo có độ chính xác cao và định kỳ hiệu chuẩn.

Sai số do phương pháp tính toán thường xuất phát từ việc bỏ qua các yếu tố ảnh hưởng. Cần xem xét đầy đủ các điều kiện thực tế.

Để giảm thiểu sai số, nên thực hiện đo đạc nhiều lần và lấy giá trị trung bình. Phương pháp này giúp kết quả đáng tin cậy hơn.

Bài tập ví dụ về tính độ cao h

Để giúp các em nắm vững công thức tính độ cao h, tôi sẽ hướng dẫn chi tiết qua các bài tập điển hình. Với hơn 20 năm kinh nghiệm giảng dạy, tôi nhận thấy việc làm nhiều bài tập sẽ giúp ghi nhớ công thức tốt hơn.

Bài tập mẫu có lời giải chi tiết

Bài 1: Một vật dao động điều hòa với phương trình x = 5cos(2πt + π/6) cm. Tính độ cao h của vật tại thời điểm t = 1/12 s.

Lời giải:

• Bước 1: Xác định biên độ A = 5 cm
• Bước 2: Thay t = 1/12 vào phương trình

x = 5cos(2π.1/12 + π/6) = 5cos(π/6 + π/6) = 5cos(π/3) = 2,5 cm

• Bước 3: Áp dụng công thức h = A
  • x = 5 - 2,5 = 2,5 cm

Các dạng bài tập thường gặp

Qua thực tế giảng dạy, tôi thường gặp 3 dạng bài tập chính:

Dạng 1: Cho phương trình dao động, tìm h tại một thời điểm
Dạng 2: Tìm h khi biết vận tốc và gia tốc
Dạng 3: Xác định h từ công thức tính biên độ góc là gì

Phương pháp giải nhanh

Khi giải các bài tập về độ cao, tôi thường hướng dẫn học sinh áp dụng quy tắc sau:

Xác định ngay biên độ A từ phương trình dao động. Sau đó tính li độ x tại thời điểm cần tìm. Cuối cùng áp dụng công thức h = A

• x sẽ ra kết quả nhanh chóng và chính xác.

Một mẹo nhỏ là vẽ đồ thị dao động để hình dung rõ hơn về độ cao h. Điều này giúp học sinh tránh nhầm lẫn giữa các đại lượng.

FAQ: Câu hỏi thường gặp về cách tính độ cao h

Khi tính toán độ cao h, nhiều học sinh thường gặp khó khăn và thắc mắc. Tôi sẽ giải đáp một số câu hỏi phổ biến nhất để giúp các em nắm vững hơn.

Làm sao để tránh sai sót khi tính độ cao h?

Để tính chính xác độ cao h, việc đầu tiên là xác định rõ tam giác cần tính. Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn giữa các cạnh.

Cách tốt nhất là vẽ hình tam giác thật rõ ràng và ghi chú các số liệu đã cho. Điều này giúp tránh nhầm lẫn giữa các cạnh và góc.

Ngoài ra, cần kiểm tra kết quả bằng cách thế ngược vào công thức ban đầu. Nếu kết quả phù hợp thì độ cao h đã tính đúng.

Có thể áp dụng công thức này cho mọi trường hợp không?

Công thức tính độ cao h áp dụng được cho mọi tam giác. Tuy nhiên cần lưu ý một số trường hợp đặc biệt.

Với tam giác vuông, độ cao h trùng với một cạnh góc vuông. Khi đó không cần dùng công thức phức tạp.

Với tam giác tù, độ cao h có thể nằm ngoài tam giác. Trong trường hợp này vẫn áp dụng công thức bình thường nhưng cần chú ý khi vẽ hình.

Những lỗi phổ biến khi sử dụng công thức

Lỗi thường gặp nhất là nhầm lẫn giữa các cạnh khi thay số vào công thức. Học sinh cần ghi nhớ cạnh đáy và độ cao tương ứng.

Một số em quên bình phương các số hạng hoặc nhầm dấu trong công thức. Tôi khuyên các em nên viết từng bước tính toán.

Ngoài ra, việc không kiểm tra đơn vị đo cũng gây sai sót. Cần quy đổi các đơn vị về cùng hệ trước khi tính toán.

Việc áp dụng công thức tính độ cao h đòi hỏi sự chính xác và cẩn thận trong từng bước tính toán. Các thành phần trong công thức có mối liên hệ chặt chẽ và ý nghĩa vật lý rõ ràng. Thông qua các bài tập mẫu và phương pháp giải nhanh, người học dễ dàng nắm vững cách vận dụng công thức này vào thực tế. Việc tránh các sai sót thường gặp giúp kết quả tính toán luôn chính xác.