Thuộc lòng công thức thấu kính phân kì và ứng dụng trong quang học

Công thức thấu kính phân kì giúp xác định chính xác vị trí và tính chất ảnh của vật qua thấu kính. Các phương pháp tính toán tiêu cự, độ tụ được trình bày chi tiết kèm ví dụ minh họa. Bài viết cung cấp hướng dẫn vẽ ảnh và giải bài tập thực tế về thấu kính phân kì.

Công thức thấu kính phân kì và các thành phần cơ bản

Thấu kính phân kì là loại thấu kính có khả năng làm phân tán các tia sáng song song với trục chính sau khi đi qua thấu kính. Đây là một trong những kiến thức quan trọng trong quang học.

Công thức cơ bản của thấu kính phân kì được biểu diễn như sau:

1/f = 1/d + 1/d’

Trong đó:

• f: Tiêu cự của thấu kính (đơn vị: m)
• d: Khoảng cách từ vật đến thấu kính (đơn vị: m)
• d’: Khoảng cách từ ảnh đến thấu kính (đơn vị: m)

Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn về dấu của các đại lượng. Với thấu kính phân kì, tiêu cự f luôn mang giá trị âm. Bạn có thể tham khảo thêm công thức tính f thấu kính để hiểu rõ hơn.

Một điểm đặc biệt của thấu kính phân kì là ảnh tạo thành luôn là ảnh ảo, nhỏ hơn vật và cùng chiều với vật. Điều này giúp chúng ta dễ dàng phân biệt với thấu kính hội tụ.

Khi giải các bài tập về thấu kính phân kì, việc đầu tiên là xác định đúng dấu của các đại lượng. Sau đó áp dụng công thức trên để tìm ra kết quả chính xác.

Đặc điểm và cấu tạo của thấu kính phân kì trong quang học

Thấu kính phân kì là loại thấu kính có phần giữa mỏng hơn phần rìa. Khi ánh sáng đi qua, các tia sáng bị tách ra xa nhau tạo thành chùm phân kì.

Cấu tạo của thấu kính phân kì gồm hai mặt cong lõm hoặc một mặt phẳng và một mặt lõm. Tiêu cự của thấu kính phân kì luôn mang giá trị âm theo công thức thấu kính mỏng.

Các đặc điểm thấu kính phân kì cơ bản bao gồm độ hội tụ âm, tiêu điểm ảo và khả năng tạo ảnh ảo nhỏ hơn vật thật.

Cấu tạo và nguyên lý hoạt động của thấu kính phân kì

Thấu kính phân kì có cấu tạo đặc trưng với phần rìa dày hơn phần tâm. Điều này tạo nên hiệu ứng phân tán ánh sáng khi tia sáng đi qua.

Khi tia sáng song song với trục chính đi qua thấu kính, chúng bị khúc xạ và tách ra xa trục chính. Các tia ló có đường kéo dài cắt nhau tại tiêu điểm ảo phía trước thấu kính.

Nguyên lý này giúp thấu kính phân kì tạo ra ảnh ảo, nhỏ hơn và thẳng đứng so với vật thật.

So sánh thấu kính phân kì và hội tụ

Thấu kính phân kì và hội tụ khác nhau thế nào thể hiện qua hình dạng và tính chất quang học. Thấu kính hội tụ có phần giữa dày hơn rìa và tạo ảnh thật, trong khi thấu kính phân kì ngược lại.

Về tiêu cự, thấu kính hội tụ có tiêu cự dương và tiêu điểm thật. Ngược lại, thấu kính phân kì có tiêu cự âm và tiêu điểm ảo.

Khả năng tạo ảnh cũng khác biệt rõ rệt. Thấu kính hội tụ có thể tạo cả ảnh thật lẫn ảnh ảo, còn thấu kính phân kì chỉ tạo được ảnh ảo.

Vai trò của thấu kính phân kì trong các thiết bị quang học

Thấu kính phân kì đóng vai trò quan trọng trong việc khắc phục các tật của mắt. Nó được sử dụng làm kính mắt cho người cận thị để điều chỉnh tiêu cự.

Trong kính thiên văn Galileo, thấu kính phân kì được dùng làm thị kính. Sự kết hợp với thấu kính hội tụ giúp tạo ảnh rõ nét và đứng thẳng của vật quan sát.

Các máy chiếu phim cũng sử dụng thấu kính phân kì để điều chỉnh kích thước chùm tia sáng. Điều này giúp tối ưu chất lượng hình ảnh trên màn chiếu.

Hướng dẫn tính toán với công thức thấu kính phân kì

Thấu kính phân kì có đặc điểm làm tia sáng phân tán ra xa trục chính. Việc tính toán với loại thấu kính này đòi hỏi sự cẩn thận và chính xác.

Để tính toán chính xác với công thức thấu kính phân kì, ta cần nắm vững các quy ước về dấu và các công thức cơ bản. Tiêu cự của thấu kính phân kì luôn mang giá trị âm.

Cách tính tiêu cự và độ tụ của thấu kính phân kì

Tiêu cự của thấu kính phân kì được tính theo công thức:

f = -R/2 (với R là bán kính cong của thấu kính)

Độ tụ D của thấu kính được tính bằng nghịch đảo của tiêu cự (đơn vị đi-ốp):

D = 1/f

công thức tính độ tụ của một thấu kính giúp ta xác định khả năng hội tụ hoặc phân kì của tia sáng.

Các bước xác định vị trí và tính chất ảnh

Bước 1: Xác định vị trí vật theo công thức:
d = -u (u là khoảng cách từ vật đến thấu kính)

Bước 2: Tính khoảng cách ảnh qua công thức thấu kính:
1/f = 1/d + 1/d’

Bước 3: Tính độ bội giác:
G = -d’/d

Ví dụ minh họa về tính toán thấu kính phân kì

Cho thấu kính phân kì có tiêu cự f = -20cm. Vật thật AB cao 2cm đặt cách thấu kính 30cm.

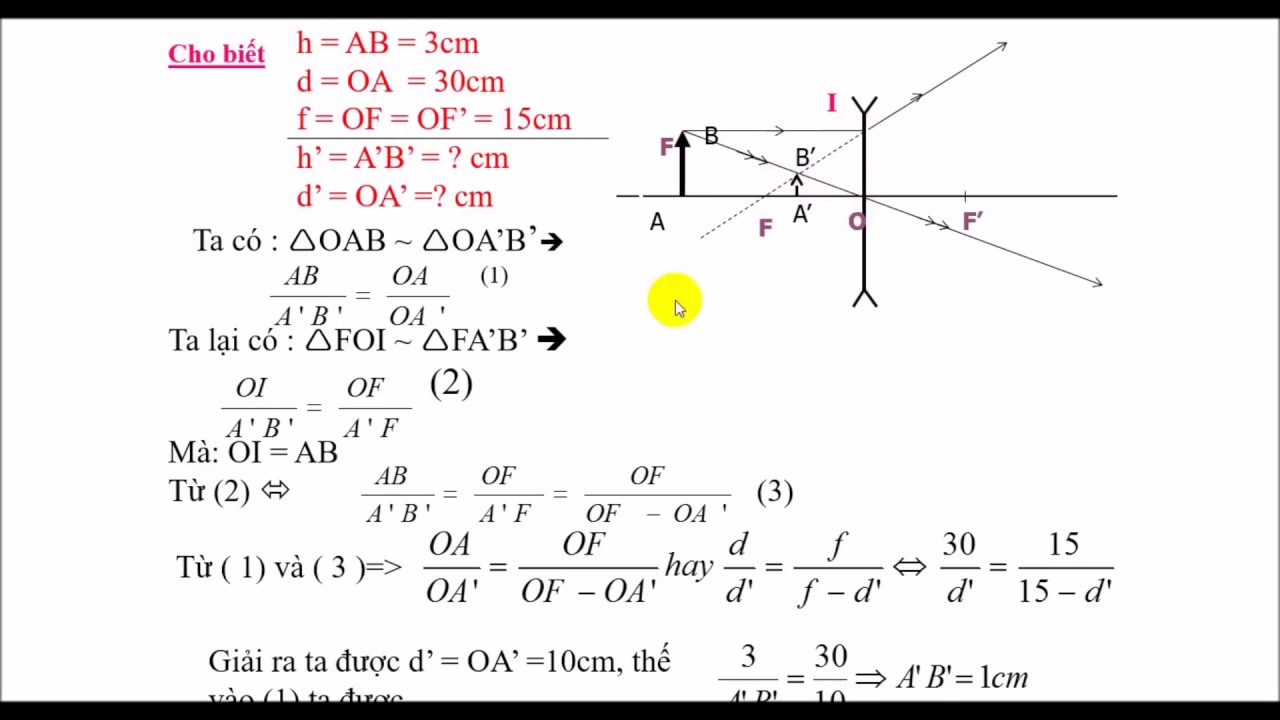
Áp dụng công thức:
1/f = 1/d + 1/d’
1/-20 = 1/30 + 1/d’

Giải ra: d’ = -12cm

Độ bội giác:
G = -d’/d = -(-12)/30 = 0,4

Vậy ảnh A’B’ cao 0,8cm, là ảnh ảo và cùng chiều với vật.

Phương pháp vẽ ảnh qua thấu kính phân kì

Thấu kính phân kì có đặc điểm làm tia sáng phân tán ra xa trục chính. Việc vẽ ảnh qua thấu kính phân kì cần tuân theo các nguyên tắc cơ bản về quang học.

Để vẽ ảnh chính xác, ta cần nắm vững các tia sáng đặc biệt và quy tắc vẽ. Khi áp dụng công thức về góc lệch trong thấu kính, ta sẽ xác định được vị trí ảnh một cách chính xác.

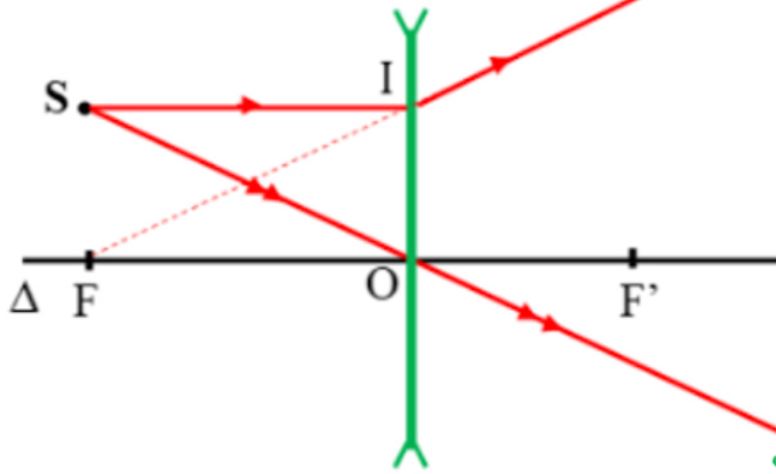
Các tia sáng đặc biệt trong thấu kính phân kì

Tia sáng song song với trục chính sau khi qua thấu kính sẽ phân kì theo hướng như xuất phát từ tiêu điểm ảnh F’.

Tia sáng đi qua quang tâm O của thấu kính sẽ đi thẳng không đổi hướng. Đây là tia quan trọng giúp xác định vị trí ảnh.

Tia sáng hướng về tiêu điểm vật F sau khi qua thấu kính sẽ đi song song với trục chính. Trong quá trình giảng dạy, tôi thường nhấn mạnh đặc điểm này.

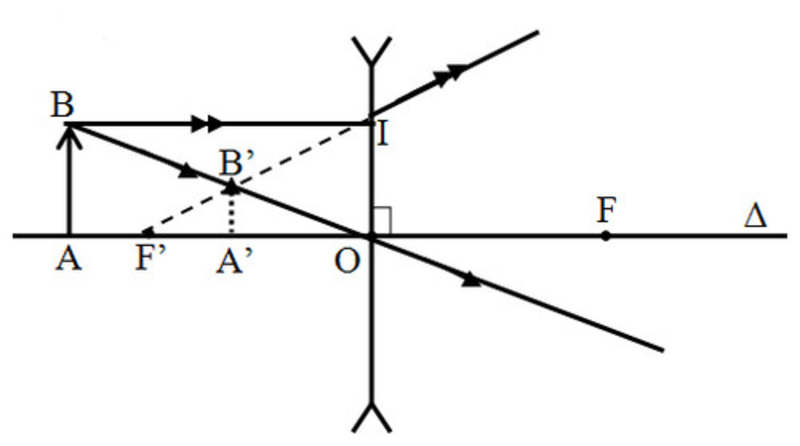
Quy tắc vẽ ảnh của vật qua thấu kính phân kì

Bước 1: Vẽ vật thẳng AB vuông góc với trục chính.

Bước 2: Vẽ 2 trong 3 tia sáng đặc biệt xuất phát từ điểm A:

• Tia song song trục chính
• Tia qua quang tâm O
• Tia hướng về tiêu điểm vật F

Bước 3: Xác định ảnh A’ tại giao điểm của các tia ló hoặc đường kéo dài của chúng.

Bài tập thực hành vẽ ảnh

Cho thấu kính phân kì có tiêu cự f = -10cm, vật thật AB cao 2cm đặt cách thấu kính 15cm.

Giải:

• Vẽ trục chính và đánh dấu F, F’, O
• Vẽ vật AB vuông góc với trục chính
• Vẽ tia song song và tia qua O
• Xác định A’ tại giao điểm
• Vẽ ảnh A’B’ vuông góc với trục chính

Kết quả cho thấy ảnh A’B’ là ảnh ảo, cùng chiều với vật và nhỏ hơn vật.

Ứng dụng thực tế và bài tập về thấu kính phân kì

Thấu kính phân kì có vai trò quan trọng trong nhiều ứng dụng thực tiễn. Tôi sẽ phân tích chi tiết các ứng dụng và cách giải bài tập về loại thấu kính này.

Ứng dụng trong đời sống và khoa học kỹ thuật

Thấu kính phân kì trong đời sống được ứng dụng rộng rãi trong các thiết bị quang học. Chúng là thành phần không thể thiếu trong kính viễn thị giúp điều chỉnh tật viễn thị.

Trong y học, thấu kính phân kì được dùng trong các thiết bị nội soi. Nó giúp mở rộng góc nhìn và quan sát được nhiều chi tiết bên trong cơ thể.

Các máy chiếu phim cũng sử dụng thấu kính phân kì để điều chỉnh kích thước hình ảnh. Điều này giúp tạo ra hình ảnh rõ nét trên màn chiếu lớn.

Bài tập mẫu và phương pháp giải

Khi giải bài tập thấu kính phân kì, cần nắm vững các công thức cơ bản. Tương tự như công thức lăng kính, ta cần xác định rõ các thông số.

Ví dụ: Một vật đặt cách thấu kính phân kì 30cm. Tiêu cự của thấu kính là -20cm. Tìm vị trí và tính chất ảnh.

Bước 1: Áp dụng công thức thấu kính 1/f = 1/d’

• 1/d
  

• 1/30
  

Các lỗi thường gặp khi giải bài tập

Học sinh thường nhầm lẫn dấu của tiêu cự thấu kính phân kì. Tiêu cự của thấu kính phân kì luôn mang giá trị âm.

Một lỗi phổ biến khác là quên kiểm tra tính chất của ảnh. Ảnh qua thấu kính phân kì luôn là ảnh ảo, cùng chiều và nhỏ hơn vật.

Việc vẽ đường truyền tia sáng cũng gây khó khăn. Cần vẽ ít nhất 2 tia đặc biệt để xác định vị trí ảnh chính xác.

FAQ: Câu hỏi thường gặp về thấu kính phân kì

Các câu hỏi thường gặp về thấu kính phân kì giúp học sinh nắm vững kiến thức cơ bản. Tôi sẽ giải đáp những thắc mắc phổ biến nhất sau 20 năm giảng dạy môn Vật lý.

Cách phân biệt thấu kính phân kì và hội tụ

Thấu kính phân kì có đặc điểm dễ nhận biết là phần giữa mỏng hơn phần rìa. Khi sờ vào bề mặt, bạn sẽ thấy phần trung tâm lõm xuống.

Ngược lại, thấu kính hội tụ có phần giữa dày hơn phần rìa và phần trung tâm lồi lên. Điều này tạo ra sự khác biệt về đường đi của tia sáng.

Cách đơn giản nhất để phân biệt là đặt thấu kính cách tờ giấy khoảng 20cm. Nếu ảnh thu được nhỏ hơn vật thì đó là thấu kính phân kì.

Những sai lầm khi sử dụng công thức thấu kính phân kì

Sai lầm phổ biến nhất là quên đặt dấu âm cho tiêu cự f của thấu kính phân kì. Tiêu cự của thấu kính phân kì luôn mang giá trị âm.

Nhiều học sinh cũng nhầm lẫn khi xác định chiều của ảnh. Ảnh qua thấu kính phân kì luôn cùng chiều với vật và là ảnh ảo.

Một lỗi khác là áp dụng sai công thức phóng đại. Độ phóng đại của thấu kính phân kì luôn nhỏ hơn 1, tức là ảnh luôn nhỏ hơn vật.

Mẹo ghi nhớ công thức thấu kính phân kì

Tôi thường hướng dẫn học sinh ghi nhớ công thức thông qua hình ảnh “ba anh em”: 1/f = 1/d’

• 1/d. Ba phân số này luôn đi cùng nhau.

Để nhớ dấu của tiêu cự, liên tưởng đến chữ P trong “Phân kì” giống như dấu trừ (-). Vì vậy tiêu cự f luôn mang dấu âm.

Một cách khác là liên hệ với thực tế: Thấu kính phân kì làm tia sáng phân tán ra xa trục chính nên tiêu điểm nằm về phía trái của thấu kính, do đó f < 0.

Việc áp dụng công thức thấu kính phân kì đòi hỏi sự hiểu biết chính xác về cấu tạo và đặc điểm của loại thấu kính này. Các công thức tính toán tiêu cự, độ tụ và phương pháp vẽ ảnh là kiến thức nền tảng trong quang học. Thấu kính phân kì có vai trò quan trọng trong nhiều thiết bị quang học và ứng dụng thực tiễn. Nắm vững các quy tắc tính toán và phương pháp vẽ ảnh giúp giải quyết hiệu quả các bài tập về thấu kính phân kì.