Tìm hiểu công thức phản xạ toàn phần và các ứng dụng trong thực tiễn
Công thức phản xạ toàn phần giúp giải thích cơ chế truyền ánh sáng trong cáp quang. Hiện tượng này xảy ra khi ánh sáng đi từ môi trường chiết suất lớn sang nhỏ. Các ứng dụng thực tiễn của nó có trong y học và công nghệ thông tin.
Công thức phản xạ toàn phần và ý nghĩa vật lý
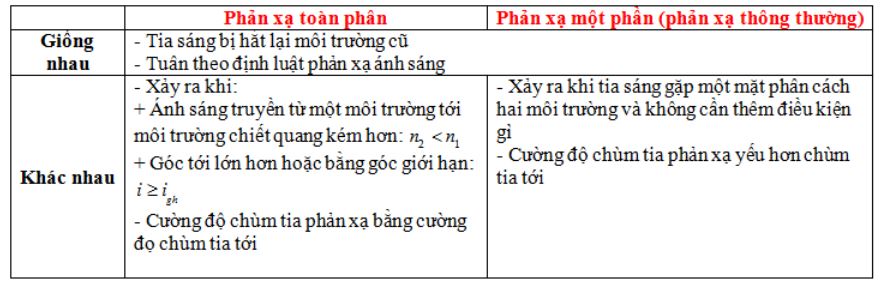
Hiện tượng phản xạ toàn phần là khi ánh sáng truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém và góc tới lớn hơn góc giới hạn. Lúc này, tia sáng sẽ phản xạ hoàn toàn trở lại môi trường ban đầu.
Công thức phản xạ toàn phần được xác định thông qua góc giới hạn φgh theo công thức:
sin φgh = n2/n1
Trong đó:
- φgh là góc giới hạn phản xạ toàn phần
- n1 là chiết suất của môi trường chiết quang hơn
- n2 là chiết suất của môi trường chiết quang kém
Qua 20 năm giảng dạy, tôi thường ví von hiện tượng này giống như một tấm gương hoàn hảo. Khi góc tới lớn hơn góc giới hạn, tia sáng bị “bật” ngược lại như bóng cao su va vào tường.
Ứng dụng quan trọng của hiện tượng này là trong cáp quang viễn thông. Tín hiệu ánh sáng truyền trong lõi thủy tinh được phản xạ toàn phần liên tục, giúp thông tin đi xa mà không bị suy hao.
Một ví dụ thực tế là khi nhìn từ dưới mặt nước lên, ta thấy mặt nước như một tấm gương phản chiếu. Đây chính là do góc nhìn của ta lớn hơn góc giới hạn, tạo nên hiện tượng phản xạ toàn phần.
Điều kiện xảy ra hiện tượng phản xạ toàn phần trong môi trường quang học
Điều kiện phản xạ toàn phần là yếu tố quyết định để tia sáng bị phản xạ hoàn toàn tại mặt phân cách giữa hai môi trường trong suốt. Hiện tượng này có ý nghĩa quan trọng trong các ứng dụng quang học như cáp quang và kính lăng kính.
Để hiểu rõ hơn về hiện tượng này, chúng ta cần phân tích hai điều kiện cơ bản. Việc nắm vững các điều kiện này giúp tính toán chính xác công thức tính quang thông và các bài toán liên quan.
Điều kiện về môi trường truyền ánh sáng
Ánh sáng phải truyền từ môi trường chiết quang nhiều hơn sang môi trường chiết quang ít hơn. Điều này có nghĩa chiết suất môi trường thứ nhất (n1) phải lớn hơn chiết suất môi trường thứ hai (n2).
Trong thực tế giảng dạy, tôi thường lấy ví dụ về tia sáng truyền từ nước (n = 1,33) ra không khí (n = 1). Học sinh dễ dàng hình dung vì đây là hiện tượng thường gặp trong cuộc sống.
Điều kiện về góc tới
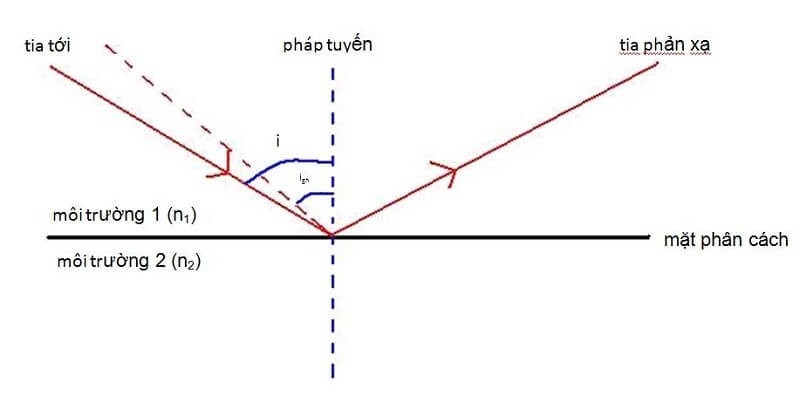
Góc tới i phải lớn hơn góc tới hạn ih của hai môi trường đó. Khi góc tới bằng góc tới hạn, tia khúc xạ sẽ đi sát mặt phân cách giữa hai môi trường.
Nếu góc tới nhỏ hơn góc tới hạn, ánh sáng sẽ khúc xạ bình thường. Ngược lại, khi góc tới lớn hơn góc tới hạn, tia sáng sẽ bị phản xạ toàn phần.
Công thức tính góc tới hạn
Công thức tính góc tới hạn được biểu diễn:
sin ih = n2/n1
Trong đó:
- ih là góc tới hạn
- n1 là chiết suất môi trường thứ nhất
- n2 là chiết suất môi trường thứ hai
Ví dụ minh họa
Tính góc tới hạn khi ánh sáng truyền từ nước (n1 = 1,33) ra không khí (n2 = 1):
sin ih = 1/1,33 = 0,752
ih = 48,8°
Vậy khi góc tới i > 48,8° thì xảy ra hiện tượng phản xạ toàn phần. Đây là nguyên lý hoạt động của nhiều thiết bị quang học hiện đại.
Phương pháp xác định góc giới hạn phản xạ toàn phần
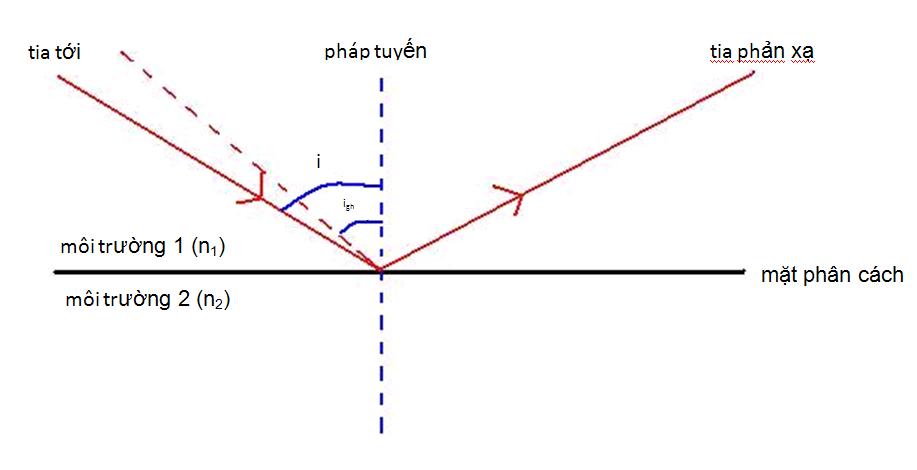
Góc giới hạn phản xạ toàn phần là góc tới nhỏ nhất để xảy ra hiện tượng phản xạ toàn phần. Khi ánh sáng truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém, góc khúc xạ sẽ lớn hơn góc tới.
Để xác định góc giới hạn, ta cần biết chiết suất của hai môi trường và áp dụng định luật Snell. Tại góc giới hạn, góc khúc xạ bằng 90 độ và tia khúc xạ nằm dọc theo mặt phân cách giữa hai môi trường.
Trong thực tế, hiện tượng phản xạ toàn phần được ứng dụng rộng rãi trong cáp quang, kính thiên văn và các thiết bị quang học khác. Tôi thường lấy ví dụ về cáp quang để giúp học sinh hiểu rõ hơn về nguyên lý này.
Các bước tính góc giới hạn
Bước 1: Xác định chiết suất của hai môi trường (n1 và n2)
Công thức tính góc giới hạn:
sin ih = n2/n1
Trong đó:
- ih là góc giới hạn
- n1 là chiết suất môi trường thứ nhất (chiết quang hơn)
- n2 là chiết suất môi trường thứ hai (chiết quang kém)
Bước 2: Thay số và tính toán
- Đưa các giá trị n1, n2 vào công thức
- Tính sin ih
- Dùng máy tính để tìm góc ih (lấy arcsin của kết quả)
Bài tập mẫu có lời giải chi tiết
Bài toán: Tính góc giới hạn khi ánh sáng truyền từ nước (n1 = 1,33) ra không khí (n2 = 1).
Lời giải:
Áp dụng công thức: sin ih = n2/n1
Thay số: sin ih = 1/1,33 = 0,752
Dùng máy tính: ih = arcsin(0,752) = 48,8°
Vậy góc giới hạn phản xạ toàn phần là 48,8°. Điều này có nghĩa nếu góc tới lớn hơn 48,8° thì ánh sáng sẽ phản xạ toàn phần, không có tia khúc xạ ra không khí.
Kinh nghiệm của tôi khi giảng dạy là luôn nhắc học sinh kiểm tra xem n1 có lớn hơn n2 không. Nếu không thỏa mãn điều kiện này thì không thể có hiện tượng phản xạ toàn phần.
Ứng dụng của hiện tượng phản xạ toàn phần trong thực tế
Ứng dụng phản xạ toàn phần đã mang lại nhiều đột phá trong công nghệ và khoa học hiện đại. Hiện tượng này giúp ánh sáng truyền đi mà không bị tổn thất năng lượng đáng kể. Tôi sẽ phân tích chi tiết các ứng dụng quan trọng nhất trong đời sống.
Cáp quang và truyền tín hiệu
Phản xạ toàn phần trong cáp quang là ứng dụng phổ biến nhất của hiện tượng này. Cáp quang gồm lõi thủy tinh trong suốt và vỏ bọc có chiết suất thấp hơn.
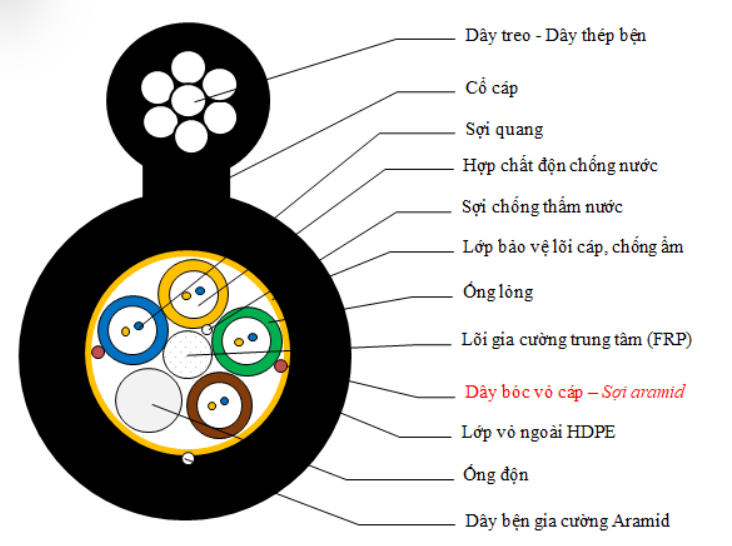
Tín hiệu ánh sáng truyền trong lõi sẽ liên tục phản xạ toàn phần tại bề mặt phân cách giữa lõi và vỏ. Nhờ đó, tín hiệu có thể truyền đi xa hàng trăm kilomet mà không bị suy giảm nhiều.
Theo số liệu từ Viện Khoa học và Công nghệ Việt Nam, tốc độ truyền tin qua cáp quang có thể đạt tới 1Tbps
- nhanh gấp hàng nghìn lần so với cáp đồng truyền thống.
Ứng dụng trong các thiết bị quang học
Kính lúp, kính hiển vi và ống nhòm đều tận dụng hiện tượng phản xạ toàn phần. Các lăng kính trong thiết bị được thiết kế để tạo góc tới lớn hơn góc giới hạn.
Điều này giúp ánh sáng phản xạ hoàn toàn mà không bị tán xạ ra ngoài. Nhờ đó hình ảnh quan sát được rõ nét và sắc nét hơn.
Trong thực tế giảng dạy, tôi thường dùng một thí nghiệm đơn giản với ly nước và laser để minh họa nguyên lý này cho học sinh hiểu rõ hơn.
Ứng dụng trong y học
Nội soi là ứng dụng quan trọng của phản xạ toàn phần trong y học. Ống nội soi sử dụng bó sợi quang học để dẫn ánh sáng vào cơ thể.
Ánh sáng phản xạ từ các mô sẽ theo đường ngược lại để tạo hình ảnh rõ nét. Kỹ thuật này giúp bác sĩ quan sát được bên trong cơ thể mà không cần phẫu thuật.
Công nghệ laser trong phẫu thuật mắt cũng áp dụng nguyên lý tương tự. Tia laser được dẫn chính xác đến vị trí cần điều trị nhờ hệ thống gương và lăng kính phản xạ toàn phần.
Bài tập về phản xạ toàn phần và phương pháp giải
Phản xạ toàn phần là hiện tượng quang học thường gặp trong thực tế. Tôi sẽ hướng dẫn các em giải các dạng bài tập phản xạ toàn phần phổ biến.
Để giải tốt các bài tập này, các em cần nắm vững điều kiện xảy ra phản xạ toàn phần. Đó là góc tới phải lớn hơn góc tới hạn và ánh sáng truyền từ môi trường chiết suất lớn sang môi trường chiết suất nhỏ hơn.
Bài tập về xác định góc tới hạn
Bài tập xác định góc tới hạn thường yêu cầu tính góc tới hạn khi biết chiết suất của hai môi trường. Công thức tính góc tới hạn là:
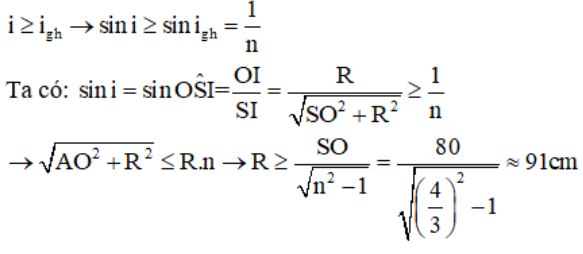
sin(ih) = n2/n1
Trong đó:
- ih là góc tới hạn
- n1 là chiết suất môi trường thứ nhất (môi trường chiết suất lớn)
- n2 là chiết suất môi trường thứ hai (môi trường chiết suất nhỏ)
Ví dụ: Tính góc tới hạn khi ánh sáng truyền từ nước (n1 = 1,33) ra không khí (n2 = 1).
Ta có: sin(ih) = 1/1,33 = 0,752
Vậy ih = 48,8°
Bài tập về chiết suất môi trường
Dạng bài tập này yêu cầu xác định chiết suất phản xạ toàn phần của môi trường khi biết góc tới hạn. Đây là dạng bài ngược lại với dạng trên.
Công thức tính chiết suất:
n1 = n2/sin(ih)
Khi ánh sáng truyền từ môi trường này sang môi trường khác, ta luôn có:
n1.sin(i1) = n2.sin(i2)
Kinh nghiệm giải là cần xác định rõ môi trường có chiết suất lớn và nhỏ trước khi áp dụng công thức.
Bài tập tổng hợp
Bài tập tổng hợp thường kết hợp nhiều kiến thức về phản xạ toàn phần. Các em cần:
- Xác định điều kiện xảy ra phản xạ toàn phần
- Vẽ sơ đồ đường truyền của tia sáng
- Áp dụng các công thức tính góc tới hạn và chiết suất
Một mẹo nhỏ khi giải bài tập là luôn kiểm tra kết quả bằng cách thế ngược lại vào công thức ban đầu.
FAQ: Câu hỏi thường gặp về phản xạ toàn phần
- Định luật phản xạ toàn phần là gì?
Khi ánh sáng truyền từ môi trường chiết quang hơn sang môi trường chiết quang kém, nếu góc tới lớn hơn góc giới hạn thì tia sáng sẽ phản xạ toàn phần trở lại môi trường ban đầu.
- Công thức phản xạ toàn phần được tính như thế nào?
Góc giới hạn phản xạ toàn phần được tính theo công thức:
sin ih = n2/n1
Trong đó:
- ih: góc giới hạn
- n1: chiết suất môi trường thứ nhất (môi trường chiết quang hơn)
- n2: chiết suất môi trường thứ hai (môi trường chiết quang kém)
- Tại sao cần có góc tới lớn hơn góc giới hạn?
Khi góc tới nhỏ hơn góc giới hạn, ánh sáng vẫn khúc xạ sang môi trường thứ hai. Chỉ khi góc tới lớn hơn góc giới hạn, hiện tượng phản xạ toàn phần mới xảy ra.
- Ứng dụng của phản xạ toàn phần là gì?
Phản xạ toàn phần được ứng dụng trong cáp quang truyền tín hiệu, kính thiên văn phản xạ và các thiết bị quang học khác để truyền dẫn ánh sáng với tổn hao rất nhỏ.
- Làm thế nào để xác định môi trường chiết quang hơn và kém?
Môi trường có chiết suất lớn hơn được gọi là môi trường chiết quang hơn. Ví dụ: nước (n=1,33) chiết quang hơn không khí (n=1).
Các kiến thức về công thức phản xạ toàn phần giúp giải thích nhiều hiện tượng quang học trong tự nhiên. Việc nắm vững công thức tính góc tới hạn, điều kiện xảy ra và các ứng dụng thực tế tạo nền tảng quan trọng cho học sinh tiếp cận các bài toán phức tạp hơn. Đặc biệt, hiện tượng này đóng vai trò then chốt trong công nghệ truyền tín hiệu quang học và các thiết bị y tế hiện đại.
Bài viết liên quan

Học công thức số phóng đại vật thật và ứng dụng trong quang học
Tìm hiểu công thức số phóng đại với vật thật trong quang học, cách tính và ứng dụng trong kính lúp, kính hiển vi, gương và thấu kính. Giải thích chi tiết các đặc điểm và ý nghĩa vật lý.

Ghi nhớ công thức tính vị trí ảnh và các phương pháp xác định chính xác
Tìm hiểu công thức tính vị trí ảnh trong quang học với các phương pháp xác định qua gương phẳng, gương cầu và thấu kính. Hướng dẫn chi tiết kèm bài tập minh họa.

Thông tin về công thức kính thiên văn và cách tính toán cơ bản
Tổng hợp các công thức kính thiên văn cơ bản về độ phóng đại, tiêu cự, khẩu độ, độ phân giải và góc trường. Hướng dẫn chi tiết cách tính toán kèm ví dụ thực tế.
Ghi nhớ công thức thấu kính mỏng và các ứng dụng trong quang học
Tìm hiểu công thức thấu kính mỏng với cách tính tiêu cự, độ tụ và số phóng đại. Phân tích chi tiết các trường hợp tạo ảnh qua thấu kính hội tụ, phân kỳ cùng ứng dụng thực tiễn.

Học công thức tính quang thông tổng và ứng dụng trong chiếu sáng
Tìm hiểu công thức tính quang thông tổng và các thành phần cơ bản trong đo lường ánh sáng. Hướng dẫn chi tiết cách tính, đo đạc và ứng dụng thực tế cho đèn LED.

Ghi nhớ công thức tính độ phóng đại kính hiển vi và cách áp dụng
Tìm hiểu công thức tính độ phóng đại ảnh của kính hiển vi qua cấu tạo, nguyên lý hoạt động và cách áp dụng trong thực tế. Bài giảng chi tiết dành cho học sinh phổ thông.

