Ghi nhớ công thức lực hồi phục và các ứng dụng trong vật lý

Công thức lực hồi phục giúp xác định độ lớn và chiều của lực tác động lên vật đàn hồi. Lực này đóng vai trò quan trọng trong các dao động cơ học. Các ứng dụng thực tế của nó xuất hiện trong thiết kế giảm xóc xe và đệm lò xo.

Công thức lực hồi phục là gì?

Lực hồi phục là lực xuất hiện khi vật đàn hồi bị biến dạng và có xu hướng đưa vật về trạng thái ban đầu. Công thức lực hồi phục được biểu diễn bằng định luật Hooke:

F = -kx

Trong đó:

• F là lực hồi phục (đơn vị N)
• k là độ cứng của lò xo (đơn vị N/m)
• x là độ biến dạng của vật (đơn vị m)
• Dấu (-) thể hiện chiều của lực hồi phục ngược với chiều biến dạng

Qua 20 năm giảng dạy, tôi thường ví von lực hồi phục giống như “sức bật” của một lò xo. Khi bạn ấn lò xo xuống, nó sẽ nén lại và có xu hướng bật ngược trở lại vị trí cũ.

Để dễ nhớ công thức, các bạn có thể liên tưởng: k là “khả năng” chống lại biến dạng của vật, còn x là mức độ “xê dịch” khỏi vị trí cân bằng. Nhân hai yếu tố này ta được lực hồi phục F.

Ví dụ thực tế: Khi kéo một lò xo có độ cứng k = 100 N/m ra khỏi vị trí cân bằng một đoạn x = 0,2m, lực hồi phục sẽ là:
F = -k.x = -(100)(0,2) = -20N
Dấu (-) cho thấy lực hồi phục có chiều ngược với chiều kéo lò xo.

Các thành phần và ý nghĩa trong công thức lực hồi phục

Công thức lực hồi phục được biểu diễn bởi biểu thức:

F = -k.Δl

Đây là một trong những công thức quan trọng trong cơ học.

Lực hồi phục là lực có xu hướng kéo vật về vị trí cân bằng ban đầu. Giống như một chiếc lò xo bị nén, nó luôn muốn trở về trạng thái tự nhiên.

Trong quá trình giảng dạy, tôi thường ví von lực này như “sức mạnh nội tại” của vật, giúp học sinh dễ hình dung hơn về bản chất của nó.

Hệ số độ cứng k và ý nghĩa vật lý

Hệ số k đặc trưng cho độ cứng của vật đàn hồi. Đơn vị của k là N/m (Newton trên mét).

Giá trị k càng lớn thì vật càng khó biến dạng. Tôi thường lấy ví dụ về hai loại lò xo: lò xo cứng trong bút bi và lò xo mềm trong đồ chơi trẻ em.

Khi giải các bài tập liên quan đến công thức định luật bảo toàn đông lượng lớp 10, việc xác định chính xác hệ số k rất quan trọng.

Độ biến dạng Δl và cách xác định

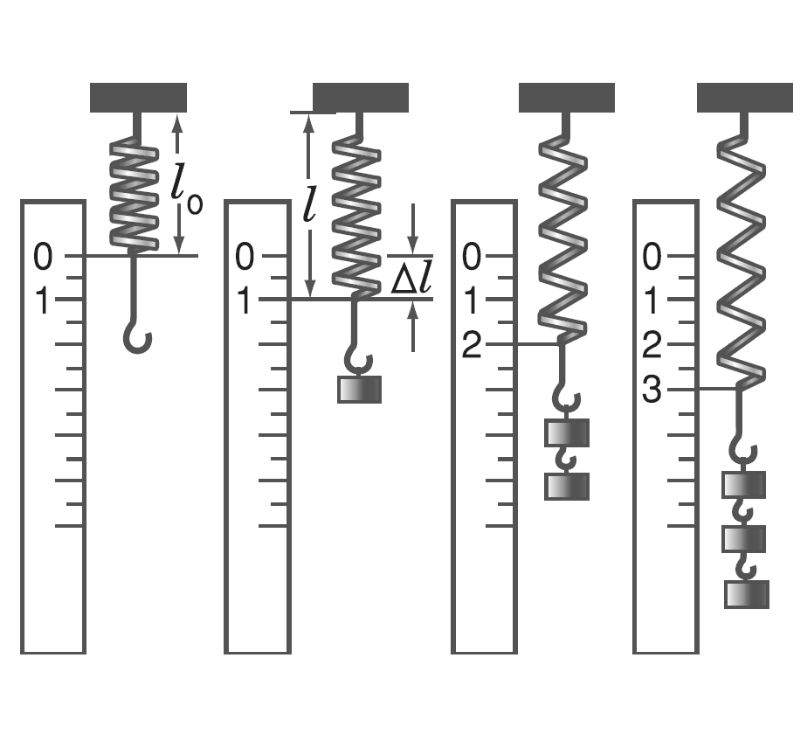
Độ biến dạng Δl là hiệu số giữa chiều dài khi bị biến dạng và chiều dài ban đầu của vật. Đơn vị tính bằng mét (m).

Công thức tính độ biến dạng:

Δl = l

• l₀

Trong đó:

• l: chiều dài sau khi biến dạng
• l₀: chiều dài ban đầu

Để xác định chính xác Δl, cần đo đạc cẩn thận và sử dụng thước có độ chính xác phù hợp.

Dấu âm trong công thức và nguyên nhân

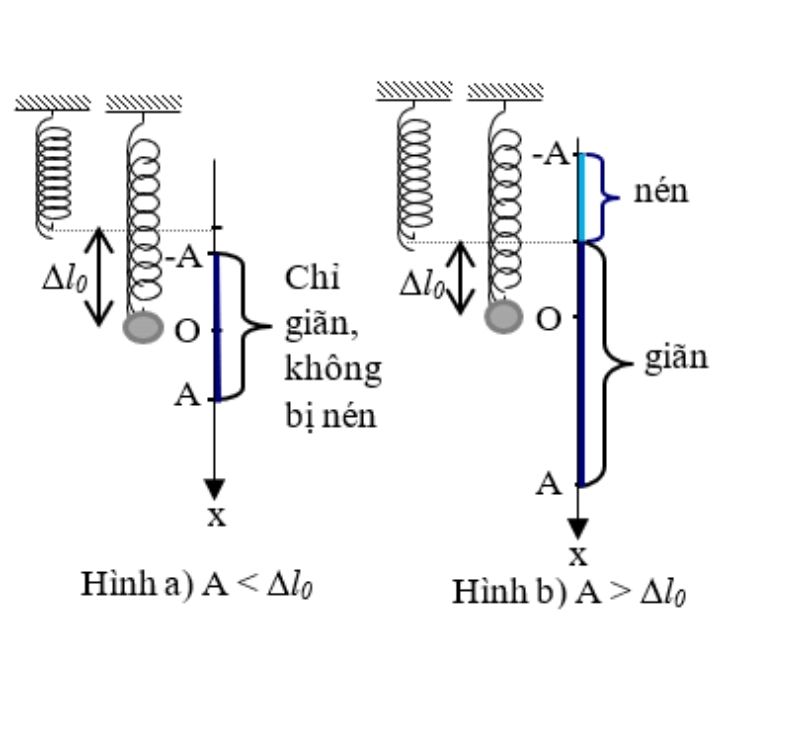
Dấu âm trong công thức tính lực phục hồi thể hiện chiều của lực luôn ngược với chiều biến dạng.

Khi vật bị kéo dãn (Δl > 0), lực hồi phục hướng về phía làm vật co lại. Ngược lại, khi vật bị nén (Δl < 0), lực hồi phục có xu hướng đẩy vật ra.

Qua 20 năm giảng dạy, tôi nhận thấy nhiều học sinh thường bỏ qua dấu âm. Điều này dẫn đến sai lầm nghiêm trọng khi xác định chiều của lực.

Ứng dụng của lực hồi phục trong thực tế và kỹ thuật

Lực hồi phục đóng vai trò quan trọng trong nhiều ứng dụng kỹ thuật và đời sống. Nguyên lý hoạt động dựa trên khả năng phục hồi trạng thái ban đầu của vật liệu đàn hồi khi chịu tác động lực.

Các ứng dụng phổ biến bao gồm hệ thống giảm xóc xe, đệm lò xo và thiết bị đo lường. Tôi sẽ phân tích chi tiết từng ứng dụng cụ thể.

Con lắc lò xo và dao động điều hòa

Con lắc lò xo là ví dụ điển hình về dao động điều hòa dưới tác dụng của lực hồi phục. Khi kéo vật nặng ra khỏi vị trí cân bằng, lò xo sinh ra lực kéo vật về vị trí ban đầu.

Trong cách tính mạch lc, dao động điều hòa của con lắc lò xo được ứng dụng để tạo ra mạch cộng hưởng điện từ. Đây là nguyên lý cơ bản của các thiết bị thu phát sóng.

Tôi thường ví von con lắc lò xo như một người nhảy dây

• luôn có xu hướng trở về vị trí cân bằng sau mỗi lần nhảy lên xuống.

Các thiết bị giảm xóc và đệm

Hệ thống giảm xóc xe máy và ô tô sử dụng lò xo để hấp thụ và giảm chấn động. Khi xe đi qua ổ gà, lò xo bị nén và sau đó giãn ra để đưa xe về vị trí cân bằng.

Đệm lò xo trong nệm và ghế sofa cũng hoạt động theo nguyên lý tương tự. Chúng biến dạng khi chịu tải trọng và phục hồi khi tải trọng được gỡ bỏ.

Theo nghiên cứu của Viện Khoa học Vật liệu, các loại lò xo thép không gỉ có khả năng chịu tải và phục hồi tốt nhất, tuổi thọ trung bình 10-15 năm.

Ứng dụng trong máy đo lực

Cân lò xo là thiết bị đo lực đơn giản dựa trên độ giãn của lò xo. Độ giãn tỷ lệ thuận với lực tác dụng theo định luật Hooke.

Các máy đo lực hiện đại kết hợp lò xo với cảm biến điện tử để cho kết quả chính xác hơn. Tôi thường hướng dẫn học sinh thực hành với cân lò xo để hiểu rõ mối quan hệ giữa lực và độ biến dạng.

Trong phòng thí nghiệm, việc hiệu chuẩn cân lò xo rất quan trọng để đảm bảo độ chính xác của phép đo. Cần kiểm tra định kỳ và thay thế khi lò xo bị mất đàn hồi.

Bài tập và phương pháp giải về lực hồi phục

Lực hồi phục là một khái niệm quan trọng trong vật lý, liên quan trực tiếp đến dao động điều hòa. Việc nắm vững công thức lực hồi phục giúp giải quyết nhiều bài tập phức tạp.

Khi giải các bài tập về lực hồi phục, ta thường phải kết hợp với công thức lực li tâm và công thức lực lorenxo để có lời giải hoàn chỉnh.

Các dạng bài tập thường gặp

Dạng 1: Xác định biên độ dao động dựa vào lực hồi phục cực đại. Đây là dạng bài tập cơ bản nhất về lực hồi phục.

Dạng 2: Tính năng lượng dao động của vật thông qua lực hồi phục. Dạng này đòi hỏi hiểu rõ mối quan hệ giữa lực và năng lượng.

Dạng 3: Xác định vị trí của vật khi biết lực hồi phục tại thời điểm t. Bài tập này cần vận dụng phương trình dao động điều hòa.

Phương pháp giải và mẹo làm bài

Bước đầu tiên là xác định chiều của lực hồi phục. Lực luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lệch x.

Công thức cơ bản cần nhớ:
F = -kx
Trong đó: k là độ cứng của lò xo, x là độ lệch khỏi vị trí cân bằng.

Khi giải bài tập phức tạp, cần vẽ sơ đồ lực để phân tích rõ các thành phần lực tác dụng lên vật.

Bài tập minh họa có lời giải chi tiết

Bài toán: Một vật khối lượng 100g dao động điều hòa với biên độ 5cm. Tại li độ 3cm, lực hồi phục có độ lớn 1,2N. Tính chu kỳ dao động của vật.

Lời giải:
Bước 1: Áp dụng công thức F = -kx
Tại x = 0,03m: |F| = k.|x| → 1,2 = k.0,03 → k = 40 (N/m)

Bước 2: Tính chu kỳ dao động
T = 2π√(m/k) = 2π√(0,1/40) = 0,314 (s)

Vậy chu kỳ dao động của vật là 0,314 giây.

FAQ: Câu hỏi thường gặp về lực hồi phục

Lực hồi phục là một khái niệm quan trọng trong vật lý. Tôi sẽ giải đáp những thắc mắc phổ biến về lực hồi phục mà học sinh thường gặp phải.

Sự khác biệt giữa lực hồi phục và lực đàn hồi

Lực đàn hồi xuất hiện khi vật bị biến dạng đàn hồi, có xu hướng đưa vật về hình dạng ban đầu. Còn lực hồi phục tác dụng lên vật để đưa vật về vị trí cân bằng.

Lực đàn hồi tuân theo định luật Hooke, tỷ lệ thuận với độ biến dạng. Trong khi đó, lực hồi phục phụ thuộc vào vị trí của vật so với vị trí cân bằng.

Mối quan hệ giữa lực hồi phục và năng lượng thế

Năng lượng thế là năng lượng tích trữ trong vật do vị trí của nó. Lực hồi phục có thể tính được từ đạo hàm của năng lượng thế:

F = -dU/dx

Trong đó:

• F là lực hồi phục
• U là năng lượng thế
• x là độ dịch chuyển

Dấu trừ cho thấy lực hồi phục luôn hướng về vị trí cân bằng, nơi năng lượng thế đạt cực tiểu.

Các yếu tố ảnh hưởng đến độ lớn lực hồi phục

Độ lớn của lực hồi phục phụ thuộc vào nhiều yếu tố khác nhau. Qua 20 năm giảng dạy, tôi nhận thấy học sinh dễ nhớ nhất khi phân tích từng yếu tố.

Yếu tố đầu tiên là độ lệch khỏi vị trí cân bằng. Vật càng xa vị trí cân bằng, lực hồi phục càng lớn.

Yếu tố thứ hai là đặc tính của hệ dao động. Ví dụ với con lắc lò xo, độ cứng k của lò xo quyết định độ lớn lực hồi phục theo công thức F = -kx.

Việc áp dụng công thức lực hồi phục đóng vai trò quan trọng trong nghiên cứu chuyển động của vật. Các thành phần trong công thức như hệ số độ cứng k và độ biến dạng Δl tạo nên mối quan hệ tuyến tính giữa lực và độ biến dạng. Công thức này giải thích nhiều hiện tượng vật lý phổ biến và ứng dụng rộng rãi trong thiết kế các thiết bị kỹ thuật như con lắc lò xo, giảm xóc và đệm.