Ghi nhớ công thức độ hụt khối đơn giản, nhanh chóng

Tìm hiểu công thức tính độ hụt khối và vận dụng thành thạo chúng vào các bài tập kiểm tra. Đây là một trong những kiến thức quan trọng giúp bạn đạt được thành tích tốt trong kỳ thi sắp tới.

Độ hụt khối là gì?

Độ hụt khối hay còn gọi là độ hụt khối của hạt nhân là sự chênh lệch của khối lượng thực tế của hạt nhân với tổng khối lượng của neutron và proton tạo ra nó. Trong vật lý, độ hụt khối có ký hiệu là m.

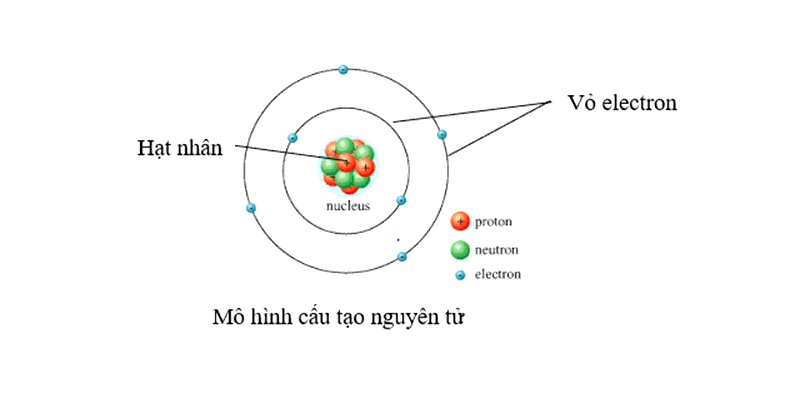
công thức xác định độ hụt khối
Cấu tạo của một hạt nhân

Độ hụt khối càng lớn thì năng lượng liên kết càng lớn và ngược lại. Đây là một trong những nhân tố quan trọng ảnh hưởng đến tính chất của hạt nhân và quyết định đến mức độ phản ứng, phân rã,.. của chúng.

Công thức tính độ hụt khối

Công thức tính độ hụt khối như sau: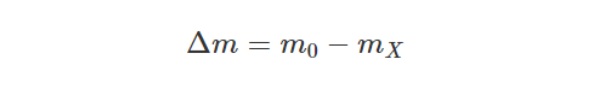công thức độ hụt khối

Trong đó:

  • m là độ hụt khối
  • m0 là khối lượng của các proton và notron khi chưa liên kết thành hạt nhân
  • mx là khối lượng của hạt nhân X

Ngoài ra, ban có thể dễ dàng xác định độ hụt khối bằng biểu thức sau:

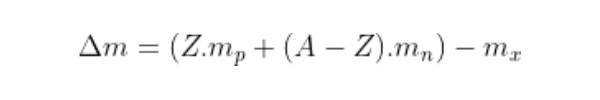
công thức tính độ hụt khối

Trong đó:

  • m là độ hụt khối
  • mx là khối lượng của hạt nhân X
  • Zmp là khối lượng của Z hạt proton
  • (A-Z)mn là khối lượng của hạt Notron

Bài tập vận dụng công thức độ hụt khối

Câu 1: Chọn câu phát biểu đúng:

  1. Đồng vị là các nguyên tử mà hạt nhân của chúng có số khối A bằng nhau.
  2. Đồng vị là các nguyên tử mà hạt nhân của chúng có số proton bằng nhau, số nơtron khác nhau.
  3. Đồng vị là các nguyên tử mà hạt nhân của chúng có số nơtron bằng nhau, số proton khác nhau.
  4. Đồng vị là các nguyên tử mà hạt nhân của chúng có khối lượng bằng nhau.

Bài giải:

Đáp án B

Đồng vị là các nguyên tử mà hạt nhân của chúng có cùng số proton, nhưng khác nhau số nơtron.

Câu 2: Chọn phát biểu đúng:

  1. Năng lượng liên kết là toàn bộ năng lượng của nguyên tử gồm động năng và năng lượng nghỉ.
  2. Năng lượng liên kết là năng lượng tỏa ra khi các nuclon liên kết với nhau tạo thành hạt nhân.
  3. Năng lượng liên kết là năng lượng toàn phần của nguyên tử tính trung bình trên số nuclon.
  4. Năng lượng liên kết là năng lượng liên kết các electron và hạt nhân nguyên tử.

Đáp án B

Câu 3: Phát biểu nào sau đây là ?

  1. Hạt nhân nguyên tử được cấu tạo từ các proton.
  2. Hạt nhân nguyên tử được cấu tạo từ các nơtron.
  3. Hạt nhân nguyên tử được cấu tạo từ các proton và các nơtron.
  4. Hạt nhân nguyên tử được cấu tạo từ các proton, notron và electron.

Đáp án C

Hạt nhân nguyên tử được cấu tạo từ các proton và các nơtron.

Câu 4: Phát biểu nào sau đây là khi nói về cấu tạo của hạt nhân nguyên tử?

  1. Hạt nhân được cấu tạo từ các nuclôn.
  2. Có hai loại nuclôn là proton và nơtron.
  3. Số proton trong hạt nhân đúng bằng số electron trong nguyên tử.
  4. Cả A, B và C đều đúng.

Đáp án D

Cả ba ý trên đều đúng.

Câu 5: Phát biểu nào sau đây là ?

  1. Hạt nhân nguyên tử được cấu tạo từ các proton.
  2. Hạt nhân nguyên tử được cấu tạo từ các nơtron.
  3. Hạt nhân nguyên tử được cấu tạo từ các proton và các nơtron.
  4. Hạt nhân nguyên tử được cấu tạo từ các proton, notron và electron.

Đáp án C

Hạt nhân nguyên tử được cấu tạo từ các proton và các nơtron.

Câu 6: Cho khối lượng của hạt proton, notron và đơteri D12 lần lượt là: 1,0073u; 1,0087u và 2,0136u. Biết 1u = 931,5 MeV/c2. Năng lượng liên kết của hạt nhân  D12 là:

  1. 2,24 MeV.    B. 3,06 MeV.
  2. 1,12 MeV.    D. 4,48 MeV.

Bài giải

Ta có: ΔE = Δm.c2 = (mp + mn

  • mD)c2 = (1,0073 + 1,0087 - 2,0136).931,5 = 2,2356 (MeV). Đáp án A.

Câu 7: Cho khối lượng của hạt proton; nơtron và hạt nhân đơteri D12  lần lượt là 1,0073u; 1,0087u và 2,0136u. Biết 1u = 931,5 MeV/c2. Năng lượng liên kết riêng của hạt nhân đơteri D12  là:

  1. 3,06 MeV/nuclôn.
  2. 1,12 MeV/nuclôn.
  3. 2,24 MeV/nuclôn.
  4. 4,48 MeV/nuclôn.

Bài giải

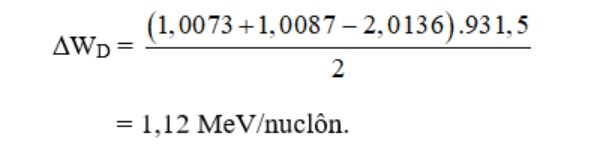
độ hụt khối

Câu 8:

Khối lượng nguyên tử của radi Ra226 là m = 226,0254u.

a) Hãy chỉ ra thành phần cấu tạo hạt nhân Rađi?

b) Tính ra kg của 1 mol nguyên tử Rađi, khối lượng 1 hạt nhân, 1 mol hạt nhân Rađi?

c) Tìm khối lượng riêng của hạt nhân nguyên tử cho biết bán kính hạt nhân được tính theo công thức r = ro.A1/3, với ro = 1,4.10-15 m, A là số khối.

d) Tính năng lượng liên kết của hạt nhân, năng lượng liên kết riêng, biết mP = 1,007276u, mn = 1,008665u ; me = 0,00549u ; 1u = 931 MeV/c2 .

Bài giải

a) Hãy chỉ ra thành phần cấu tạo hạt nhân Rađi?

Khối lượng một mol : mmol = m.NA

=> mmol = 375,7.10-27. 6,022.1023

=> mmol= 226,17.10-3 kg = 226,17 g

b) Tính ra kg của 1 mol nguyên tử Rađi, khối lượng 1 hạt nhân, 1 mol hạt nhân Rađi?

Khối lượng một hạt nhân : mHN = m

  • Zme

=> mHN = 259,977u = 3,7524.10-25kg

Khối lượng 1mol hạt nhân : mmolHN = mNH.NA

=> mmolHN = 0,22589kg

c) Tìm khối lượng riêng của hạt nhân nguyên tử cho biết bán kính hạt nhân được tính theo công thức r = ro.A1/3, với ro = 1,4.10-15 m, A là số khối.

Thể tích hạt nhân: V = 4πr3/3 = 4πro3A/ 3 .

Khối lượng riêng của hạt nhân: 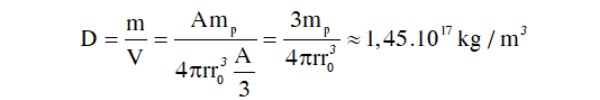độ hụt khối hạt nhân

d) d) Tính năng lượng liên kết của hạt nhân, năng lượng liên kết riêng, biết mP = 1,007276u, mn = 1,008665u ; me = 0,00549u ; 1u = 931 MeV/c2 .

Năng lượng liên kết của hạt nhân là:

Ta có: ΔE = Δmc2

=> ΔE = {ZmP + (A

  • Z)mN - m}c2

=> ΔE = 1,8107uc2 = 1,8107.931 = 1685 MeV

Năng lượng liên kết riêng của hạt nhân là = EA = 7,4557 MeV/nu

Kết luận

Những công thức tính độ hụt khối được tổng hợp chuẩn xác và trình bày dễ hiểu. Tham khảo một vài bài tập ứng dụng để nâng cao khả năng vận dụng của bạn một cách dễ dàng.

Bài viết liên quan

  • Hiểu rõ công thức tính năng lượng ion hóa và quy luật biến thiên

    Hiểu rõ công thức tính năng lượng ion hóa và quy luật biến thiên

    Tìm hiểu chi tiết công thức tính năng lượng ion hóa, các yếu tố ảnh hưởng và quy luật biến thiên trong bảng tuần hoàn. Bao gồm bảng tra cứu và so sánh giữa kim loại, phi kim.

  • Khái quát công thức định luật phóng xạ và các ứng dụng thực tiễn

    Khái quát công thức định luật phóng xạ và các ứng dụng thực tiễn

    Tìm hiểu chi tiết công thức định luật phóng xạ với các thành phần cơ bản, cách tính số hạt nhân, độ phóng xạ và ứng dụng thực tế qua các ví dụ minh họa đơn giản.

  • Hiểu rõ công thức tính bán kính quỹ đạo dừng và ứng dụng thực tế

    Hiểu rõ công thức tính bán kính quỹ đạo dừng và ứng dụng thực tế

    Tìm hiểu chi tiết công thức tính bán kính quỹ đạo dừng của electron, các yếu tố ảnh hưởng và phương pháp giải bài tập từ cơ bản đến nâng cao dành cho học sinh phổ thông.

  • Tổng quan công thức tính khối lượng hạt nhân và cách áp dụng cơ bản

    Tổng quan công thức tính khối lượng hạt nhân và cách áp dụng cơ bản

    Tìm hiểu công thức tính khối lượng hạt nhân và cách áp dụng trong hóa học. Hướng dẫn chi tiết phương pháp tính toán, các thành phần cấu tạo và mối quan hệ với khối lượng nguyên tử.

  • Tìm hiểu công thức tính entropy và ứng dụng trong nhiệt động lực học

    Tìm hiểu công thức tính entropy và ứng dụng trong nhiệt động lực học

    Tìm hiểu chi tiết công thức tính entropy qua các dạng bài tập cơ bản trong nhiệt động lực học. Giải thích khái niệm, ý nghĩa vật lý và phương pháp áp dụng công thức entropy hiệu quả.

  • Công thức tính hằng số phóng xạ và các ứng dụng trong phản ứng hạt nhân

    Công thức tính hằng số phóng xạ và các ứng dụng trong phản ứng hạt nhân

    Tìm hiểu công thức tính hằng số phóng xạ và các thành phần liên quan. Hướng dẫn chi tiết cách xác định chu kỳ bán rã, hoạt độ, khối lượng chất phóng xạ kèm ví dụ thực tế.

    • [trafficuser_check_code]