Ghi nhớ công thức dao động điều hòa chuẩn xác – Cách xác định hằng số đơn giản

Công thức dao động điều hòa là một dạng phương trình với các hằng số và biến số. Tham khảo các bài tập vận dụng kèm lời giải chuẩn xác để ghi nhớ và nắm rõ hơn bản chất của dao động điều hòa.

Dao động điều hòa là gì?

Dao động điều hòa là chuyển động qua lại một vị trí cân bằng. Quỹ đạo của chuyển động điều hòa là một đoạn thẳng, có li độ là hàm cos hoặc hàm sin của thời gian.

Ví dụ. Chuyển động của xích đu quay quanh trục, chuyển động của bập bênh, chuyển động của con thuyền nhấp nhô trên mặt nước khi được neo cố định,…

Công thức dao động điều hòa

Phương trình dao động điều hòa có dạng tổng quát như sau:

x = Acos(wt + φ )

Trong đó:

• A,w, là các hằng số
• x là li độ của vật
• A là biên độ dao động của vật
• w là tần số góc của dao động
• φ là pha ban đầu của dao động
• (ωt + φ) là pha dao động tại thời điểm t, gọi tắt là pha của li độ

Cách xác định các hằng số

Dưới đây là một số công thức liên quan giúp bạn xác định các hằng số trong phương trình dao động điều hòa một cách đơn giản hơn.

1/ Cách xác định biên độ dao động A

Biên độ dao động được xác định bằng công thức:

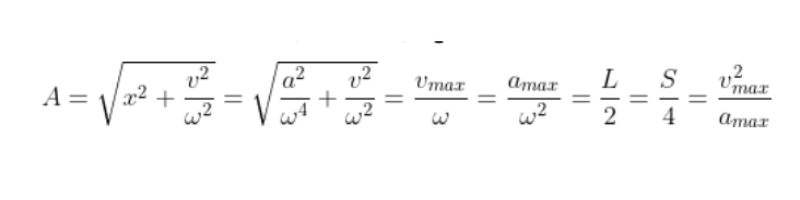
Trong đó:

• L là chiều dài quỹ đạo của dao động
• S là quãng đường trong 1 chu kỳ

2/ Cách tìm tần số góc w

Bạn có thể xác định w thông qua công thức sau:

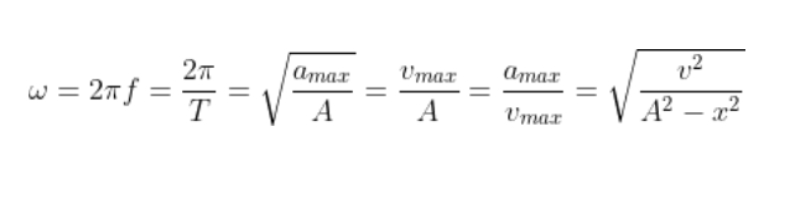
Trong đó:

• T là chu kỳ của giao động
• F là tần số của dao động
• v là vận tốc
• A là biên độ giao động của vật

3/ Cách xác định pha ban đầu của dao động

Với t = 0, ta có hệ phương trình: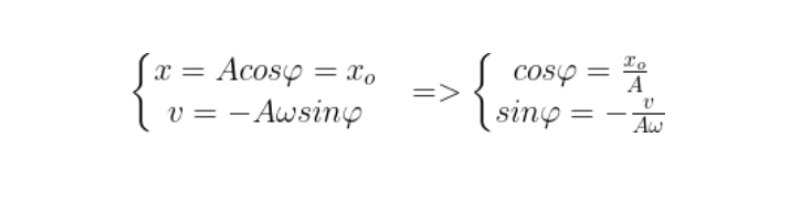

Ứng dụng của dao động điều hòa trong cuộc sống

Dao động điều hòa được ứng dụng trong nhiều lĩnh vực trong cuộc sống. Bạn có thể bắt gặp chúng trong các phát minh từ đơn giản đến phức tạp.

• Đồng hồ quả lắc: Với các loại đồng hồ treo tường dạng cổ điển, chu kỳ dao động không đổi của quả lắc được dùng để xác định sự thay đổi của thời gian.
• Hệ thống treo xe: Dao động điều hòa từ lò xo và xung lực từ mặt đường giúp giảm xóc, tạo sự êm ái và ổn định cho xe trong quá trình di chuyển.
• Kỹ thuật điện và điện từ: Lò xo điện từ, tụ điện tạo ra dao động điều hòa, giúp truyền và nhận tín hiệu. Chúng được ứng dụng trong các thiết bị di động, truyền hình
  • viễn thông.
• Kỹ thuật xây dựng: Áp dụng dao động điều hòa để xác định khả năng chịu tác động như gió, động đất,…
• Âm nhạc: Sử dụng dao động điều hòa từ dây đàn và cột khí bên trong để tạo ra âm thanh cho các nhạc cụ.
• Y học: Các máy đo rung tim là ứng dụng của dao động điều hòa để ghi lại hoạt động của tim, từ đó giúp chẩn đoán kịp thời những bất thường.

Bài tập vận dụng công thức dao động điều hòa

Vận dụng công thức dao động điều hòa để giải các bài tập dưới đây.

Bài tập 1

Phương trình của dao động điều hòa là x = 2cos(5t

• π/6)(cm). Hãy cho biết biên độ, pha ban đầu, và pha ở thời điểm t của dao động.

Bài giải:

Phương trình của dao động điều hòa là x = 2cos(5t

• π/6)(cm). Từ đó, ta xác định được các thống số như sau:

• Biên độ của dao động: A = 2 (cm)

• Pha ban đầu của dao động: φ = -π/6 (rad)

• Pha ở thời điểm t của dao động: 5t - π/6 (rad)

Bài tập 2

Một vật dao động điều hòa theo phương trình x = Acos(ωt + φ).

a) Lập công thức tính vận tốc và gia tốc của vật.

b) Ở vị trí nào thì vận tốc bằng 0? Ở vị trí nào thì gia tốc bằng 0?

c) Ở vị trí nào thì vận tốc có độ dài cực đại? Ở vị trí nào thì gia tốc có độ lớn cực đại?

Bài giải:

a) Công thức vận tốc v = x'(t) = -ωAsin(ωt + φ)

Công thức gia tốc a = v'(t) = -ω^2.Acos(ωt + φ) hay a = -ω^2.x

b) Tại vị trí biên x = A hoặc x =

• A thì vận tốc v = 0.

Tại vị trí cân bằng x = 0 thì gia tốc a = 0.

c) Tại vị trí cân bằng x = 0 thì vận tốc v = ωA.

Tại vị trí biên x = A hoặc x =

• A thì gia tốc a = ω^2.A.

Bài tập 3

Cho phương trình của dao động điều hòa x =

• 5cos(4πt) (cm). Biên độ và pha ban đầu của dao động là bao nhiêu?

1. 5cm; 0 rad;
2. 5 cm; 4π rad;
3. 5 cm; (4π.t) rad;
4. 5cm; π rad;

Bài giải:

Đáp án: D. 5 cm; π rad;

• Phương trình của dao động điều hòa: x = -5cos(4πt) = 5cos(4πt + π)

• Biên độ của dao động A = 5cm.

• Pha ban đầu của dao động φ = π (rad)

Bài tập 4

Một vật dao động điều hòa theo phương trình x = 5cos(4t + 23) cm. Xác định tần số góc của dao động là.

Bài giải:

Phương trình dao động tổng quát: x=Acosωt+φcm

Phương trình dao động của vật: x=5cos4πt+2π3cm

=> Tần số góc của dao động: ω = 4π (rad/s)

Bài tập 5

Một vật dao động điều hòa có phương trình x=2cos (2πt−7π/6) cm. Xác định li độ của vật tại thời điểm t = 0,25 (s).

Bài giải:

Li độ của vật tại thời điểm t = 0,25 s là: x = 2cos(2.0,25

• 7/6) = -1 cm.

Kết luận

Những chia sẻ về công thức dao động điều hòa là kiến thức hữu ích. Lưu lại và thường xuyên ôn tập để không ngừng nâng cao kết quả học tập trong thời gian sắp tới.