Điểm qua công thức chuyển động thẳng đều và các dạng bài tập cơ bản

Công thức chuyển động thẳng đều giúp giải quyết các bài toán về vận tốc, quãng đường và thời gian. Chúng tôi phân tích chi tiết từng công thức kèm đồ thị minh họa. Bài viết cung cấp phương pháp giải nhanh cùng các ví dụ thực tế dễ hiểu.

Công thức chuyển động thẳng đều là gì?

Công thức chuyển động thẳng đều mô tả mối quan hệ giữa quãng đường, vận tốc và thời gian trong chuyển động thẳng đều. Đây là dạng chuyển động cơ bản nhất trong vật lý.

Công thức tổng quát:

s = v.t

Trong đó:

• s: quãng đường vật đi được (m)
• v: vận tốc không đổi (m/s)
• t: thời gian chuyển động (s)

Qua 20 năm giảng dạy, tôi thường ví von công thức này như “tam giác vàng”

• biết 2 yếu tố sẽ tìm được yếu tố còn lại. Học sinh chỉ cần nhớ mối liên hệ này.

Ví dụ thực tế: Một ô tô chạy với vận tốc 60 km/h trong 2 giờ. Quãng đường xe đi được là:

s = v.t = 60 km/h × 2h = 120 km

Ngoài ra còn có công thức phụ:

v = s/t (tính vận tốc)

t = s/v (tính thời gian)

Khi giải bài tập, học sinh cần:

• Xác định rõ các đại lượng đã cho
• Chuyển đổi đơn vị về cùng hệ
• Áp dụng công thức phù hợp
• Kiểm tra kết quả có hợp lý

Đây là công thức cơ bản giúp học sinh làm quen với chuyển động thẳng đều trước khi học các dạng chuyển động phức tạp hơn.

Đặc điểm và tính chất của chuyển động thẳng đều

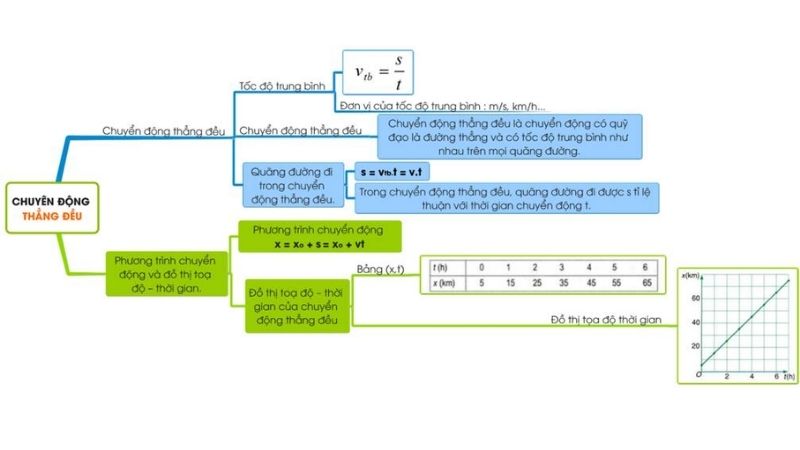
Chuyển động thẳng đều là dạng chuyển động cơ bản và đơn giản nhất trong vật lý. Các đặc điểm chuyển động thẳng đều thể hiện qua vận tốc không đổi và quỹ đạo là đường thẳng.

Để hiểu rõ hơn về loại chuyển động này, tôi sẽ phân tích chi tiết từng đặc điểm quan trọng. Việc nắm vững các đặc điểm sẽ giúp giải quyết nhiều bài toán về chuyển động.

Các đặc điểm cơ bản của chuyển động thẳng đều

Chuyển động thẳng đều có hai đặc điểm cơ bản quan trọng cần ghi nhớ. Đầu tiên là vận tốc của vật luôn không đổi theo thời gian.

Thứ hai là quỹ đạo chuyển động của vật phải là một đường thẳng. Điều này có nghĩa vật di chuyển theo một hướng xác định.

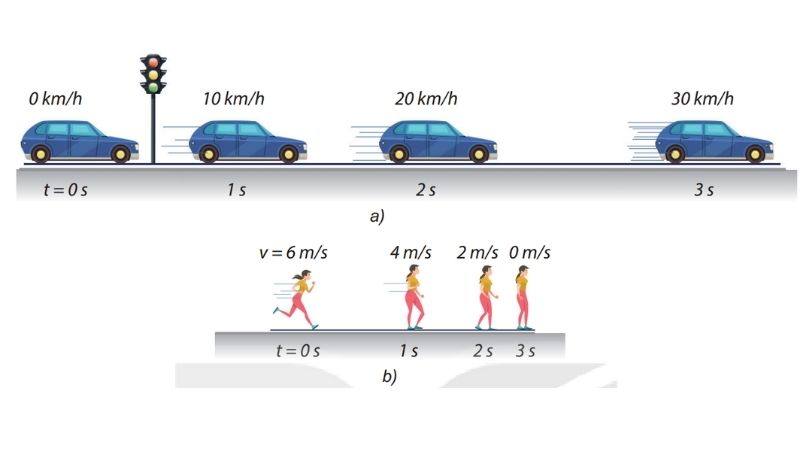
Trong thực tế, xe ô tô chạy trên đường thẳng với tốc độ không đổi là ví dụ điển hình. Tuy nhiên chuyển động thẳng đều hoàn hảo rất hiếm gặp trong tự nhiên.

Vận tốc không đổi trong chuyển động thẳng đều

Vận tốc không đổi là đặc trưng quan trọng nhất của chuyển động thẳng đều. Điều này có nghĩa độ lớn và hướng của vận tốc không thay đổi.

Công thức vận tốc trong chuyển động thẳng đều:

v = s/t

Trong đó:
v: vận tốc (m/s)
s: quãng đường (m)
t: thời gian (s)

Từ kinh nghiệm giảng dạy, tôi thường nhắc học sinh rằng vận tốc không đổi đồng nghĩa với gia tốc bằng 0. Điều này giúp phân biệt với chuyển động thẳng biến đổi đều.

Quỹ đạo chuyển động là đường thẳng

Quỹ đạo chuyển động thẳng đều phải là một đường thẳng. Vật di chuyển theo một hướng xác định không đổi.

Trong thực tế, một viên bi lăn trên mặt phẳng ngang nhẵn là ví dụ minh họa tốt. Tuy nhiên ma sát sẽ làm giảm vận tốc dần.

Để xác định quỹ đạo thẳng, ta cần xét vector vị trí của vật tại các thời điểm khác nhau. Các vector này phải cùng nằm trên một đường thẳng.

Các công thức tính toán trong chuyển động thẳng đều

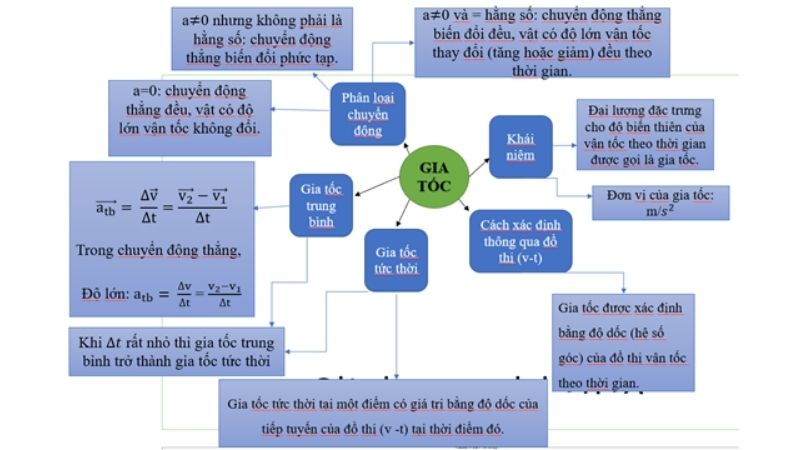
Chuyển động thẳng đều là dạng chuyển động cơ bản nhất trong vật lý. Vật chuyển động với vận tốc không đổi theo thời gian và theo một đường thẳng. Công thức chuyển động thẳng đều giúp ta tính toán các đại lượng vận tốc, quãng đường và thời gian.

Để giải các bài toán về chuyển động thẳng đều, ta cần nắm vững mối liên hệ giữa các đại lượng. Việc áp dụng công thức tính mặt phẳng nghiêng cũng rất quan trọng khi xét chuyển động trên mặt nghiêng.

Công thức tính vận tốc v = s/t

Công thức tính vận tốc chuyển động thẳng đều được biểu diễn:

v = s/t

Trong đó:

• v là vận tốc (m/s)
• s là quãng đường (m)
• t là thời gian (s)

Khi giảng dạy, tôi thường ví von vận tốc như tốc độ ăn bánh của học sinh. Nếu em ăn 1 cái bánh trong 2 phút thì vận tốc ăn bánh là 0,5 cái/phút.

Công thức tính quãng đường s = v.t

Công thức tính quãng đường chuyển động thẳng đều là:

s = v.t

Quãng đường phụ thuộc vào hai yếu tố: vận tốc và thời gian chuyển động. Nếu vận tốc càng lớn và thời gian càng dài thì quãng đường đi được càng xa.

Ví dụ thực tế: Một ô tô chạy với vận tốc 60 km/h trong 2 giờ sẽ đi được quãng đường s = 60 x 2 = 120 km.

Công thức tính thời gian t = s/v

Công thức tính thời gian chuyển động thẳng đều được xác định:

t = s/v

Thời gian chuyển động phụ thuộc vào quãng đường và vận tốc của vật. Với cùng một quãng đường, vật chuyển động càng nhanh thì thời gian càng ngắn.

Kinh nghiệm của tôi khi giải bài tập là luôn chuyển đổi đơn vị về cùng hệ đo trước khi áp dụng công thức.

Phương trình chuyển động x = x0 + v.t

Phương trình chuyển động thẳng đều có dạng:

x = x0 + v.t

Trong đó:

• x là tọa độ tại thời điểm t
• x0 là tọa độ ban đầu
• v là vận tốc
• t là thời gian

Phương trình này cho biết vị trí của vật tại mọi thời điểm. Nó rất hữu ích khi ta cần xác định vị trí tương đối giữa các vật chuyển động.

Đồ thị và biểu diễn chuyển động thẳng đều

Việc biểu diễn đồ thị chuyển động thẳng đều giúp trực quan hóa các đại lượng vật lý. Tôi thường khuyên học sinh vẽ đồ thị để nắm bắt bản chất chuyển động nhanh hơn.

Khi nghiên cứu chuyển động thẳng đều, ta cần phân tích 3 loại đồ thị cơ bản. Mỗi loại đồ thị sẽ thể hiện mối quan hệ giữa các đại lượng đặc trưng như công thức tính cường độ điện trường.

Đồ thị vận tốc

• thời gian

Đồ thị vận tốc

• thời gian của chuyển động thẳng đều là một đường thẳng song song với trục thời gian. Điều này phản ánh vận tốc không đổi trong suốt quá trình chuyển động.

Diện tích hình thang giới hạn bởi đồ thị và trục thời gian chính là quãng đường vật đi được. Đây là một trong những mẹo tôi thường chia sẻ với học sinh để tính quãng đường nhanh chóng.

Đồ thị quãng đường - thời gian

Đồ thị quãng đường

• thời gian có dạng đường thẳng đi qua gốc tọa độ. Độ dốc của đường thẳng này chính là vận tốc của chuyển động.

Trong 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn giữa đồ thị này với đồ thị vận tốc. Cách phân biệt đơn giản là đồ thị quãng đường luôn là đường xiên góc.

Đồ thị tọa độ - thời gian

Đồ thị tọa độ

• thời gian cũng là một đường thẳng xiên góc. Tuy nhiên nó không nhất thiết đi qua gốc tọa độ như đồ thị quãng đường.

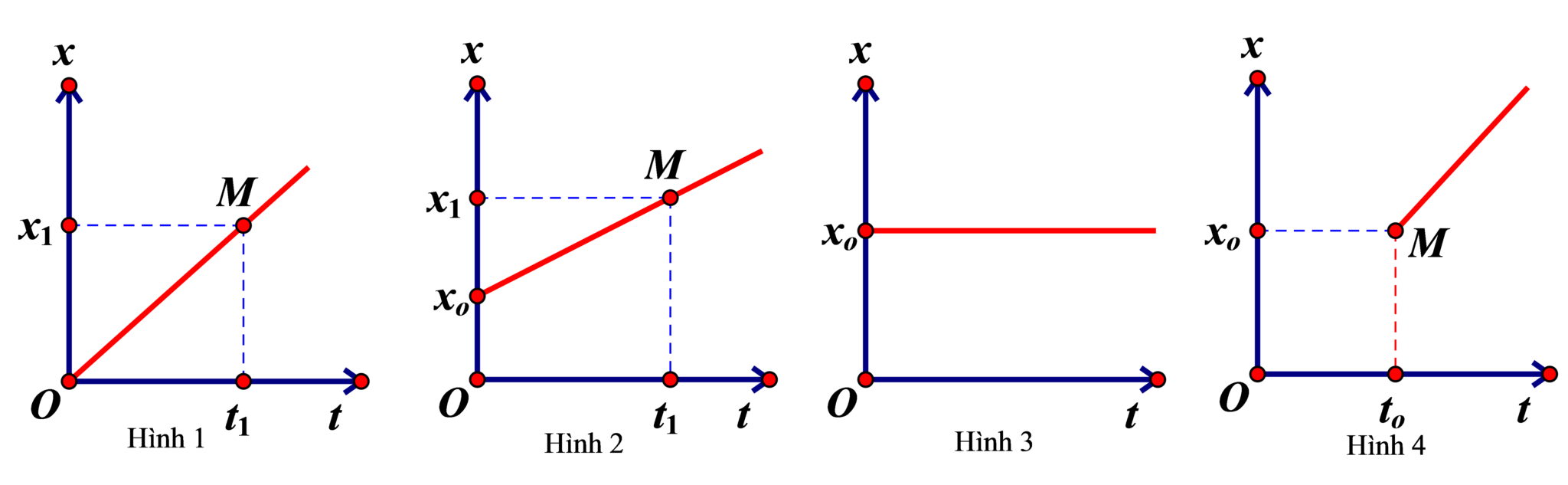
Hệ số góc của đường thẳng này cũng chính là vận tốc của chuyển động. Điểm cắt với trục tung cho biết vị trí ban đầu của vật.

Kinh nghiệm cho thấy việc phân tích đồ thị tọa độ giúp học sinh hình dung được chiều chuyển động và vị trí của vật tại mọi thời điểm.

Hướng dẫn giải các dạng bài tập chuyển động thẳng đều

Để giải các bài tập chuyển động thẳng đều, chúng ta cần nắm vững công thức cơ bản:
v = s/t (vận tốc = quãng đường/thời gian)

Từ đó có thể biến đổi thành:
s = v.t (quãng đường = vận tốc x thời gian)
t = s/v (thời gian = quãng đường/vận tốc)

Bài tập tính vận tốc

Khi giải bài tập tính vận tốc, ta áp dụng công thức v = s/t. Đơn vị vận tốc thường là m/s hoặc km/h.

Ví dụ: Một ô tô chạy được 120km trong 2 giờ với công thức chuyển động thẳng đều. Tính vận tốc của ô tô?

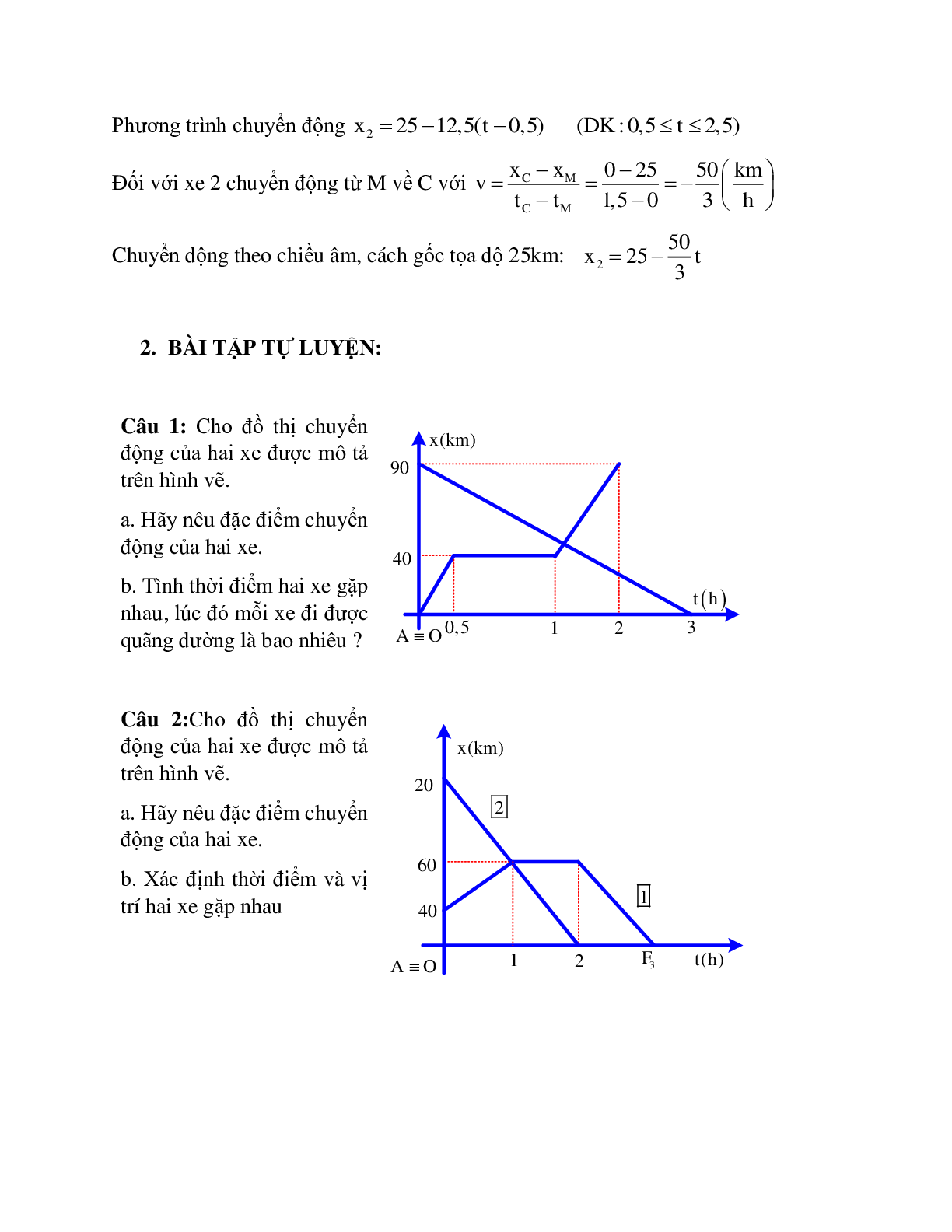
Giải:
v = s/t = 120/2 = 60 km/h

Lưu ý quan trọng: Cần quy đổi đơn vị về cùng hệ đo trước khi tính toán.

Bài tập tính quãng đường

Để tính quãng đường, ta sử dụng công thức s = v.t. Đây là dạng ví dụ chuyển động thẳng đều phổ biến.

Khi giải loại bài này, cần chú ý:

• Kiểm tra đơn vị đo
• Xác định rõ thời gian chuyển động
• Áp dụng đúng công thức s = v.t

Một mẹo nhỏ: Vẽ sơ đồ chuyển động sẽ giúp hình dung bài toán tốt hơn.

Bài tập tính thời gian

Các dạng toán chuyển động thẳng đều về thời gian thường áp dụng công thức t = s/v.

Khi một vật chuyển động với vận tốc 5 m/s và đi được quãng đường 100m, ta có:
t = 100/5 = 20s

Kinh nghiệm giải nhanh: Đặt các đại lượng vào công thức theo thứ tự để tránh nhầm lẫn.

Bài tập về đồ thị chuyển động

Đồ thị chuyển động thẳng đều có dạng đường thẳng. Độ dốc của đường thẳng chính là vận tốc.

Khi phân tích đồ thị:

• Trục hoành biểu diễn thời gian
• Trục tung biểu diễn quãng đường
• Đường thẳng càng dốc, vận tốc càng lớn

Một số đồ thị có thể giao nhau, điểm giao thể hiện hai vật gặp nhau tại cùng vị trí và thời điểm.

FAQ: Câu hỏi thường gặp về chuyển động thẳng đều

Các câu hỏi thường gặp về chuyển động thẳng đều giúp học sinh nắm vững kiến thức cơ bản. Tôi sẽ giải đáp những thắc mắc phổ biến nhất sau 20 năm giảng dạy vật lý.

Phân biệt chuyển động thẳng đều và không đều

Chuyển động thẳng đều có vận tốc không đổi theo thời gian. Vật di chuyển được quãng đường bằng nhau trong những khoảng thời gian bằng nhau.

Ngược lại, chuyển động thẳng không đều có vận tốc thay đổi. Quãng đường vật đi được trong các khoảng thời gian bằng nhau là khác nhau.

Ví dụ thực tế: Xe buýt chạy trên đường cao tốc với tốc độ 60km/h là chuyển động thẳng đều. Xe buýt trong thành phố thường xuyên tăng giảm tốc độ là chuyển động không đều.

Cách xác định vận tốc trung bình

Vận tốc trung bình được tính bằng tổng quãng đường chia cho tổng thời gian chuyển động.

Công thức: v = s/t
Trong đó:

• v là vận tốc trung bình (m/s)
• s là quãng đường (m)
• t là thời gian (s)

Kinh nghiệm của tôi khi giảng dạy là học sinh cần phân biệt rõ vận tốc trung bình và vận tốc tức thời để tránh nhầm lẫn khi giải bài tập.

Ứng dụng thực tế của chuyển động thẳng đều

Chuyển động thẳng đều xuất hiện trong nhiều hoạt động hàng ngày:

Băng chuyền trong nhà máy di chuyển với tốc độ không đổi để đảm bảo quy trình sản xuất ổn định.

Thang cuốn trong trung tâm thương mại hoạt động với vận tốc cố định giúp người dùng di chuyển an toàn.

Máy bay khi đạt độ cao ổn định sẽ bay với vận tốc không đổi để tiết kiệm nhiên liệu và đảm bảo an toàn.

Việc áp dụng các công thức chuyển động thẳng đều giúp giải quyết nhiều bài toán vật lý cơ bản. Các công thức tính vận tốc, quãng đường và thời gian có mối liên hệ chặt chẽ với nhau thông qua các đại lượng đặc trưng. Đồ thị chuyển động thẳng đều thể hiện rõ mối quan hệ tuyến tính giữa các đại lượng và là công cụ trực quan để phân tích chuyển động. Thông qua các ví dụ và bài tập thực tế, học sinh nắm vững kiến thức cơ bản về chuyển động thẳng đều.