Nắm kỹ công thức tính tần số dao động và các dạng dao động cơ bản

Công thức tính tần số dao động giúp xác định số dao động trong một đơn vị thời gian. Các dạng dao động điều hòa, tự do và cưỡng bức có công thức tính tần số khác nhau. Bài viết phân tích chi tiết các công thức kèm ví dụ thực tế dễ hiểu.

Công thức tính tần số dao động và ý nghĩa vật lý

Tần số dao động là một đại lượng vật lý quan trọng trong chuyển động dao động. Nó cho biết số dao động hoàn thành trong một đơn vị thời gian.

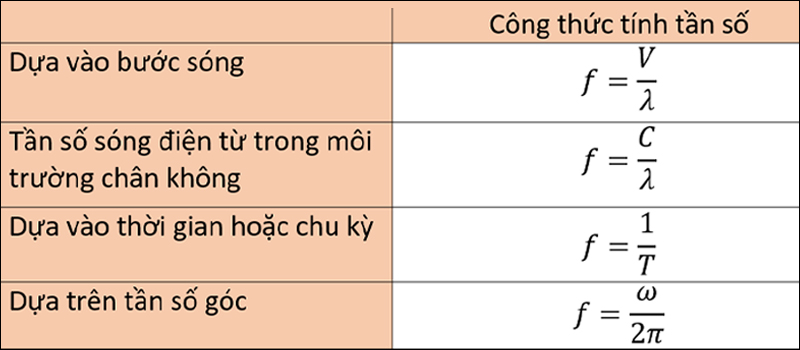
Công thức tính tần số dao động được biểu diễn như sau:

f = 1/T

Trong đó:

• f: tần số dao động (đơn vị Hz)
• T: chu kỳ dao động (đơn vị s)

Ý nghĩa vật lý của tần số dao động thể hiện qua mối quan hệ nghịch đảo với chu kỳ. Khi chu kỳ càng nhỏ, tần số càng lớn và ngược lại.

Trong quá trình giảng dạy, tôi thường lấy ví dụ về con lắc đơn để minh họa. Con lắc dao động 20 lần trong 10 giây sẽ có tần số:

f = 20/10 = 2 Hz

Điều này có nghĩa con lắc thực hiện được 2 dao động trong 1 giây.

Một lưu ý quan trọng khi sử dụng công thức là đơn vị của chu kỳ phải là giây (s). Nếu bài toán cho chu kỳ theo phút hoặc giờ, cần quy đổi về giây trước khi áp dụng công thức.

Phân biệt tần số dao động và chu kỳ dao động trong vật lý

Tần số và chu kỳ dao động là hai đại lượng quan trọng mô tả chuyển động dao động. Chúng có mối quan hệ nghịch đảo với nhau và thường xuất hiện trong các công thức vật lý.

Để hiểu rõ hơn về hai đại lượng này, tôi sẽ phân tích chi tiết từng khái niệm và ứng dụng của chúng.

Tần số dao động là gì và đơn vị đo

Tần số dao động là số dao động hoàn thành trong một đơn vị thời gian. Đơn vị đo tần số trong hệ SI là Héc (Hz).

Công thức tính tần số dao động:
f = 1/T
Trong đó:

• f là tần số dao động (Hz)
• T là chu kỳ dao động (s)

Ví dụ: Con lắc đồng hồ thực hiện 60 dao động trong 1 phút sẽ có tần số f = 1 Hz.

Chu kỳ dao động là gì và mối quan hệ với tần số

Chu kỳ dao động là khoảng thời gian để vật dao động thực hiện một dao động hoàn thành. Đơn vị đo là giây (s).

Mối quan hệ giữa chu kỳ và tần số được thể hiện qua công thức tính chu kì dao động:
T = 1/f

Trong quá trình giảng dạy, tôi thường ví von chu kỳ như thời gian để hoàn thành một vòng quay trọn vẹn của bánh xe.

Ứng dụng của tần số và chu kỳ dao động trong thực tế

Tần số và chu kỳ dao động được ứng dụng rộng rãi trong nhiều lĩnh vực:

Trong y học, các thiết bị siêu âm hoạt động dựa trên nguyên lý dao động với tần số cao từ 2-18MHz.

Trong âm nhạc, các nốt nhạc khác nhau tương ứng với các tần số dao động khác nhau của dây đàn.

Trong công nghiệp, việc kiểm tra độ rung của máy móc dựa vào đo tần số dao động để phát hiện sự cố.

Các dạng dao động và công thức tính tần số tương ứng

Dao động là một hiện tượng vật lý phổ biến trong tự nhiên và đời sống. Mỗi dạng dao động có đặc trưng và công thức tính tần số riêng biệt.

Để hiểu rõ hơn về các dạng dao động, chúng ta cần tìm hiểu về công thức dao động cơ và công thức dao động điện từ.

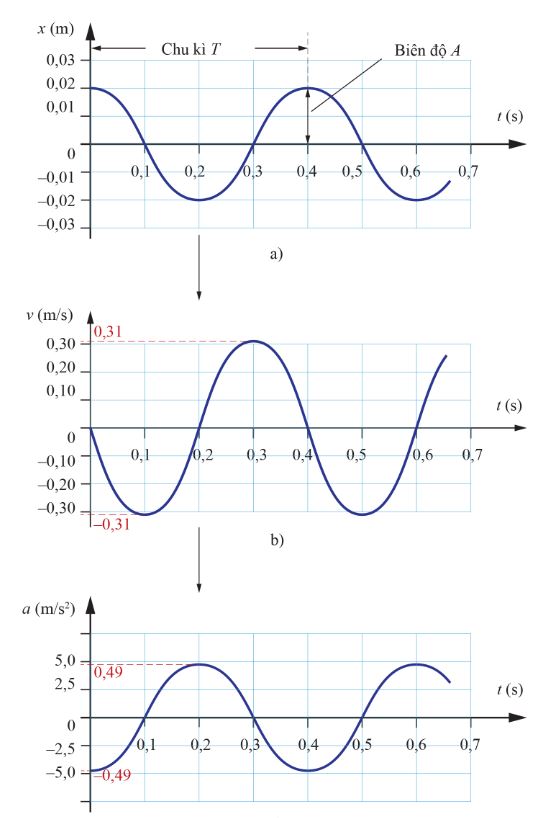
Tần số dao động điều hòa và đặc điểm

Tần số dao động điều hòa là số dao động hoàn thành trong một đơn vị thời gian. Đây là dạng dao động cơ bản nhất.

Công thức tính tần số dao động điều hòa:
f = 1/T
Trong đó:

• f là tần số dao động (Hz)
• T là chu kỳ dao động (s)

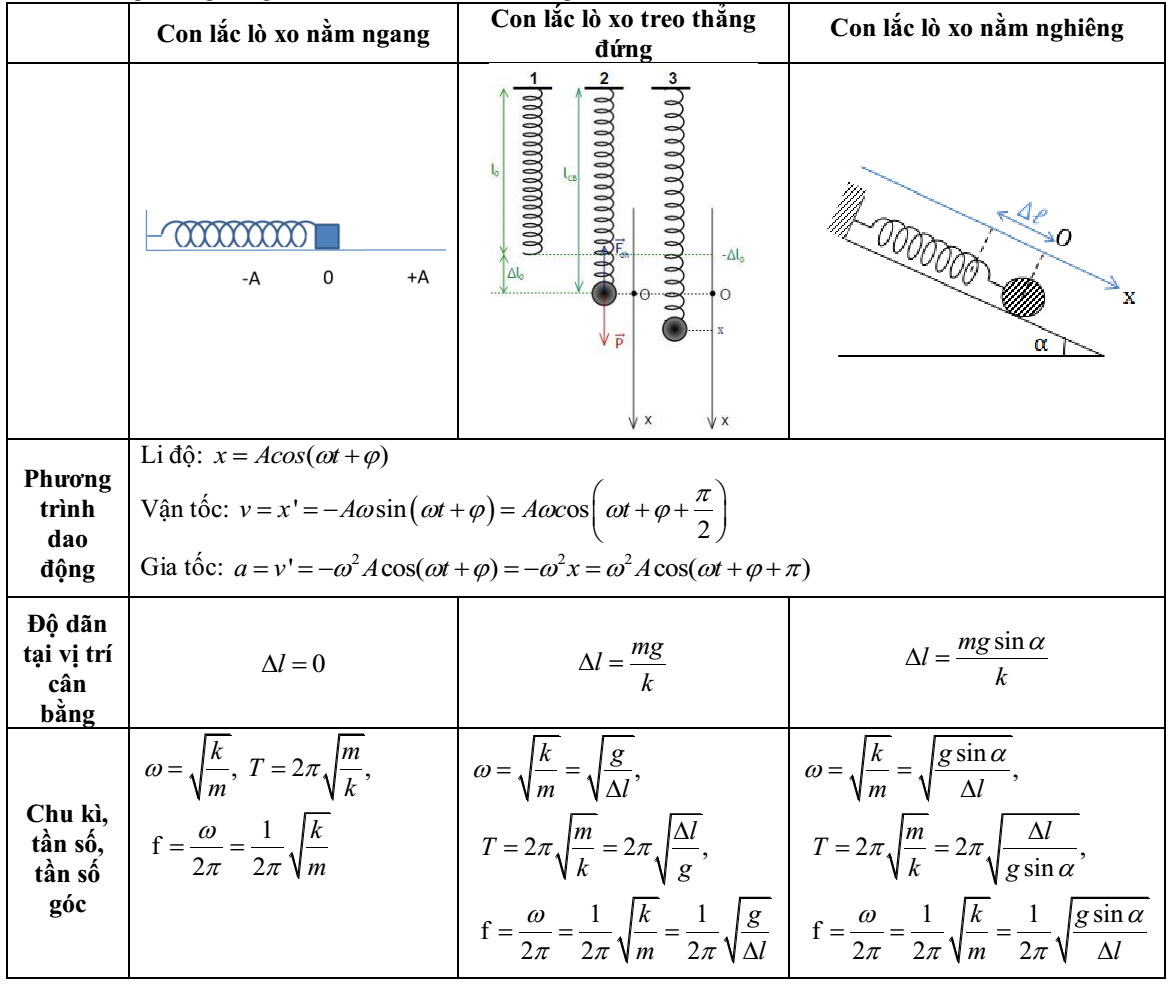
Tần số dao động tự do của hệ

Tần số dao động tự do phụ thuộc vào các thông số đặc trưng của hệ dao động. Với con lắc đơn, tần số dao động tự do phụ thuộc vào chiều dài dây và gia tốc trọng trường.

Công thức tính tần số dao động tự do:
f₀ = (1/2π)√(k/m)
Trong đó:

• k là độ cứng của lò xo
• m là khối lượng vật dao động

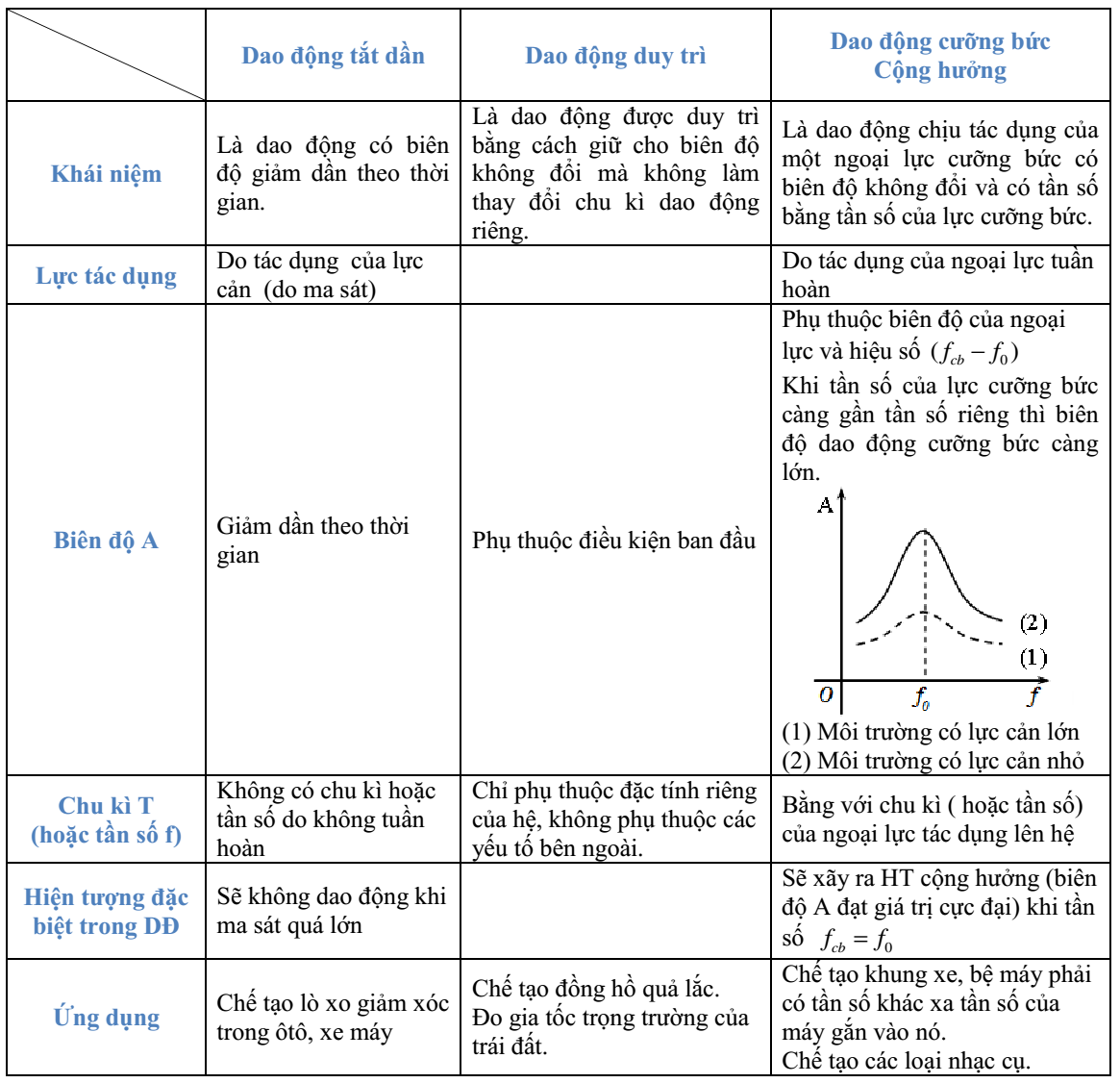
Tần số dao động cưỡng bức và hiện tượng cộng hưởng

Tần số dao động cưỡng bức xuất hiện khi có ngoại lực tác động theo chu kỳ lên hệ dao động. Khi tần số ngoại lực trùng với tần số riêng, xảy ra hiện tượng cộng hưởng.

Điều kiện xảy ra cộng hưởng

Cộng hưởng xảy ra khi tần số của ngoại lực (f) bằng tần số dao động riêng của hệ (f₀):
f = f₀

Ứng dụng và tác hại của cộng hưởng

Cộng hưởng có nhiều ứng dụng trong kỹ thuật như thiết kế nhạc cụ và máy móc. Tuy nhiên, nó cũng gây ra những tác hại nghiêm trọng.

Ứng dụng tích cực:

• Tăng biên độ dao động trong nhạc cụ
• Tối ưu hóa hoạt động của động cơ

Tác hại tiêu cực:

• Phá hủy kết cấu công trình
• Gây rung lắc máy móc quá mức

 

Tần số dao động con lắc đơn và ứng dụng

Con lắc đơn là một trong những hệ dao động cơ bản nhất trong vật lý. Nó giúp chúng ta hiểu được nhiều hiện tượng dao động trong tự nhiên và ứng dụng trong đời sống.

Việc xác định tần số dao động con lắc đơn có vai trò quan trọng trong nhiều lĩnh vực như đồng hồ quả lắc, thiết bị đo địa chấn và các công trình xây dựng chống động đất.

Công thức tính tần số dao động con lắc đơn

Công thức tính tần số dao động của con lắc đơn là:

f = 1/2π √(g/l)

Trong đó:

• f là tần số dao động (Hz)
• g là gia tốc trọng trường (m/s²)
• l là chiều dài dây treo (m)
• π ≈ 3,14

Khi giảng dạy, tôi thường nhấn mạnh với học sinh rằng tần số dao động tỷ lệ nghịch với căn bậc hai của chiều dài dây. Điều này giúp các em dễ dàng nhớ và vận dụng công thức.

Các yếu tố ảnh hưởng đến tần số dao động

Tần số dao động của con lắc đơn phụ thuộc vào hai yếu tố chính là gia tốc trọng trường và chiều dài dây treo. Việc tính toán công thức momen quán tính cũng rất quan trọng khi nghiên cứu chuyển động của con lắc.

Gia tốc trọng trường thay đổi theo vị trí địa lý sẽ ảnh hưởng đến tần số dao động. Con lắc đơn dao động nhanh hơn ở vùng cực so với vùng xích đạo.

Chiều dài dây treo là yếu tố quyết định chính. Khi tăng chiều dài, tần số dao động sẽ giảm và ngược lại.

Bài tập áp dụng về tần số dao động con lắc đơn

Một con lắc đơn có chiều dài 1m, dao động tại nơi có g = 9,8 m/s². Tính tần số dao động.

Giải:
f = 1/2π √(g/l)
f = 1/2π √(9,8/1)
f = 0,498 Hz

Kinh nghiệm của tôi khi giải bài tập là luôn kiểm tra đơn vị đo trước khi thay số. Nhiều học sinh thường mắc lỗi khi sử dụng đơn vị không đồng nhất.

FAQ: Câu hỏi thường gặp về tần số dao động

Câu hỏi 1: Tần số dao động riêng của con lắc phụ thuộc vào yếu tố nào?

Tần số dao động riêng của con lắc chỉ phụ thuộc vào đặc tính cấu tạo của hệ dao động. Với con lắc lò xo, tần số phụ thuộc vào độ cứng k của lò xo và khối lượng m của vật. Với con lắc đơn, tần số phụ thuộc vào chiều dài dây treo l và gia tốc trọng trường g.

Câu hỏi 2: Tại sao cần quan tâm đến công thức dao động tắt dần?

Dao động tắt dần là dạng dao động thực tế phổ biến nhất. Việc nắm vững công thức giúp tính toán chính xác biên độ dao động theo thời gian và dự đoán thời điểm dao động kết thúc.

Câu hỏi 3: Mối liên hệ giữa công thức tính năng lượng dao động và công thức độ biến thiên động năng?

Năng lượng dao động bằng tổng động năng và thế năng tại mọi thời điểm. Độ biến thiên động năng cho biết sự thay đổi động năng giữa hai thời điểm, giúp đánh giá sự chuyển hóa năng lượng.

Câu hỏi 4: Công thức độ biến thiên từ thông áp dụng khi nào?

Công thức được áp dụng khi có sự thay đổi từ thông qua một mạch kín, giúp tính suất điện động cảm ứng xuất hiện trong mạch theo định luật Faraday.

Việc nắm vững các công thức tính tần số dao động giúp học sinh hiểu sâu về dao động cơ học và điện từ. Các công thức này có mối liên hệ chặt chẽ với chu kỳ dao động và ứng dụng rộng rãi trong thực tế. Từ dao động điều hòa đến dao động cưỡng bức, mỗi dạng dao động đều có những đặc trưng riêng cần phân biệt. Đặc biệt với con lắc đơn, việc nắm chắc công thức và các yếu tố ảnh hưởng là nền tảng để giải quyết các bài toán dao động trong vật lý.