Ghi nhớ công thức thấu kính mỏng và các ứng dụng trong quang học

Công thức thấu kính mỏng là nền tảng quan trọng trong quang học. Thầy sẽ hướng dẫn chi tiết các công thức tính toán và ứng dụng thực tế. Các ví dụ minh họa đơn giản giúp các em nắm vững kiến thức cơ bản này.

Công thức thấu kính mỏng và các thành phần cơ bản

Trong quá trình giảng dạy, tôi nhận thấy nhiều học sinh gặp khó khăn với công thức thấu kính mỏng. Thực ra công thức này không phức tạp nếu nắm được các thành phần cơ bản.

Công thức thấu kính mỏng được biểu diễn:

1/f = 1/a + 1/a’

Trong đó:

• f là tiêu cự của thấu kính (đơn vị: cm hoặc m)
• a là khoảng cách từ vật đến thấu kính
• a’ là khoảng cách từ ảnh đến thấu kính

Một mẹo nhỏ tôi thường chia sẻ với học sinh: Hãy nhớ công thức này giống như phân số “1 chia cho f bằng tổng của 1 chia a và 1 chia a'”.

Khi áp dụng công thức, cần lưu ý quy ước dấu:

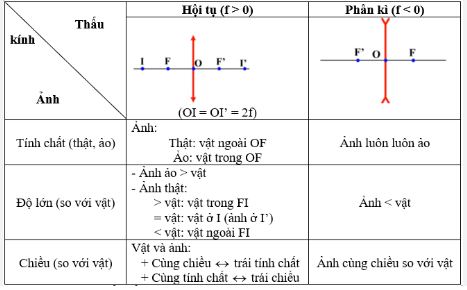
• Với thấu kính hội tụ: f > 0
• Với thấu kính phân kỳ: f < 0
• Ảnh thật: a’ > 0
• Ảnh ảo: a’ < 0

Để giúp học sinh dễ nhớ, tôi thường lấy ví dụ thực tế: Thấu kính hội tụ giống như kính lúp làm tăng kích thước chữ (f > 0), còn thấu kính phân kỳ như kính cận làm giảm kích thước (f < 0).

Nắm vững công thức và quy ước dấu sẽ giúp giải quyết được hầu hết các bài tập về thấu kính mỏng một cách dễ dàng.

Phân loại và đặc điểm của thấu kính mỏng trong quang học

Thấu kính mỏng là hệ quang học gồm hai mặt cầu trong suốt và có độ dày không đáng kể. Chúng được chia thành hai loại chính dựa vào khả năng hội tụ ánh sáng.

Mỗi thấu kính đều có các đặc trưng cơ bản như tiêu điểm, tiêu cự và độ tụ. Tiêu điểm là điểm hội tụ của các tia sáng song song với trục chính.

Trong giảng dạy, tôi thường ví von thấu kính như chiếc kính lúp mà các em hay cầm để đọc chữ nhỏ. Điều này giúp học sinh dễ hình dung về cách hoạt động của thấu kính.

Thấu kính hội tụ và các đặc trưng

Công thức thấu kính hội tụ có dạng: 1/f = 1/d + 1/d’, trong đó f là tiêu cự, d là khoảng cách vật và d’ là khoảng cách ảnh.

Thấu kính hội tụ có đặc điểm là phần giữa dày hơn phần rìa. Khi ánh sáng đi qua, các tia sáng song song với trục chính sẽ hội tụ tại tiêu điểm.

Trong thực tế, thấu kính hội tụ được ứng dụng rộng rãi trong kính lúp, kính hiển vi và máy chiếu. Tôi thường cho học sinh làm thí nghiệm với kính lúp để hiểu rõ nguyên lý.

Thấu kính phân kỳ và ứng dụng

Công thức thấu kính phân kỳ được sử dụng tương tự như công thức thấu kính phân kì. Tuy nhiên, tiêu cự f luôn mang giá trị âm.

Thấu kính phân kỳ có phần giữa mỏng hơn phần rìa. Các tia sáng song song với trục chính sau khi qua thấu kính sẽ phân kỳ.

Loại thấu kính này thường được dùng trong kính cận, ống nhòm và các thiết bị quang học khác để điều chỉnh độ phân kỳ của ánh sáng.

Cách xác định tiêu cự thấu kính phân kỳ

Để xác định tiêu cự thấu kính phân kỳ, ta cần kết hợp với một thấu kính hội tụ đã biết tiêu cự. Phương pháp này gọi là phương pháp thấu kính kép.

Qua nhiều năm giảng dạy, tôi nhận thấy học sinh thường gặp khó khăn khi xác định tiêu cự thấu kính phân kỳ. Cần phải thực hành nhiều để nắm vững kỹ năng này.

Các trường hợp tạo ảnh đặc biệt

Khi vật đặt tại tiêu điểm của thấu kính hội tụ, ảnh sẽ ở vô cực. Đây là trường hợp đặc biệt thường xuất hiện trong đề thi.

Với thấu kính phân kỳ, ảnh luôn là ảnh ảo, thẳng và nhỏ hơn vật. Điều này giải thích tại sao người cận thị nhìn vật qua kính sẽ thấy nhỏ hơn thực tế.

Kinh nghiệm cho thấy việc vẽ đường truyền tia sáng sẽ giúp học sinh hiểu rõ hơn về cách tạo ảnh trong các trường hợp đặc biệt này.

Các công thức tính toán quan trọng trong thấu kính mỏng

Thấu kính mỏng là một phần quan trọng trong quang học. Các công thức tính toán giúp xác định chính xác các thông số của thấu kính.

Công thức tính tiêu cự và độ tụ của thấu kính

Tiêu cự (f) là khoảng cách từ quang tâm đến tiêu điểm của thấu kính. Công thức tiêu cự thấu kính được tính bằng:

f = R/2(n-1)

Trong đó:

• f: tiêu cự (m)
• R: bán kính cong của thấu kính (m)
• n: chiết suất của thấu kính

Công thức tính độ tụ thấu kính được xác định:

D = 1/f

Với D là độ tụ (đơn vị đi-ốp), f là tiêu cự (m).

Mối quan hệ giữa khoảng cách vật

• ảnh và tiêu cự

Phương trình thấu kính mỏng thể hiện mối quan hệ giữa khoảng cách vật (d), khoảng cách ảnh (d’) và tiêu cự (f):

1/f = 1/d + 1/d’

Quy ước dấu:

• Thấu kính hội tụ: f > 0
• Thấu kính phân kỳ: f < 0
• Ảnh thật: d’ > 0
• Ảnh ảo: d’ < 0

Xác định số phóng đại của thấu kính

Công thức số phóng đại thấu kính cho biết tỉ lệ giữa kích thước ảnh và kích thước vật:

k = h’/h = -d’/d

Trong đó:

• k: độ phóng đại
• h’: chiều cao ảnh
• h: chiều cao vật
• d’: khoảng cách ảnh
• d: khoảng cách vật

Dấu âm (-) thể hiện ảnh ngược chiều với vật. Nếu k > 1, ảnh lớn hơn vật và ngược lại.

Công thức tiêu cự thấu kính và các công thức liên quan giúp tính toán chính xác các thông số quan trọng của thấu kính mỏng.

Phân tích các trường hợp tạo ảnh qua thấu kính mỏng

Khi ánh sáng truyền qua thấu kính mỏng, tia sáng sẽ bị khúc xạ và tạo ảnh của vật. Việc xác định vị trí và tính chất của ảnh phụ thuộc vào khoảng cách từ vật đến thấu kính.

Trước khi đi vào chi tiết, cần hiểu rõ góc lệch thấu kính là gì. Góc lệch ảnh hưởng trực tiếp đến quá trình tạo ảnh.

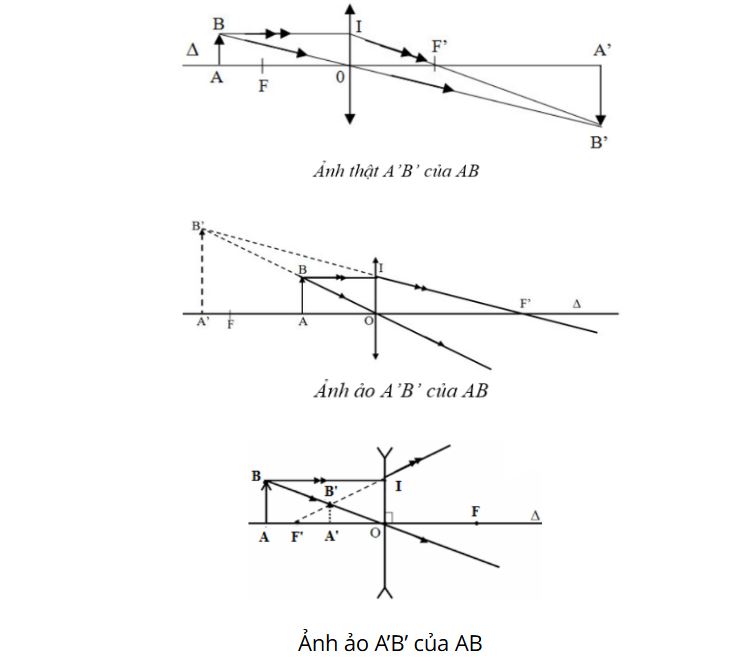
Vật thật tạo ảnh thật qua thấu kính

Khi vật đặt cách thấu kính một khoảng lớn hơn tiêu cự, ta có công thức vật thật ảnh thật thấu kính cơ bản:

1/f = 1/d + 1/d’

Trong đó:

• f là tiêu cự thấu kính
• d là khoảng cách từ vật đến thấu kính
• d’ là khoảng cách từ ảnh đến thấu kính

Ảnh thật luôn nằm phía bên kia thấu kính so với vật và có thể thu được trên màn chắn.

Vật thật tạo ảnh ảo qua thấu kính

Trường hợp vật đặt gần thấu kính hơn tiêu cự, ta áp dụng công thức vật thật ảnh ảo thấu kính:

1/f = 1/d

• 1/|d’|

Ảnh ảo cùng phía với vật và không thể thu được trên màn chắn. Tuy nhiên, ta có thể nhìn thấy ảnh này khi nhìn qua thấu kính.

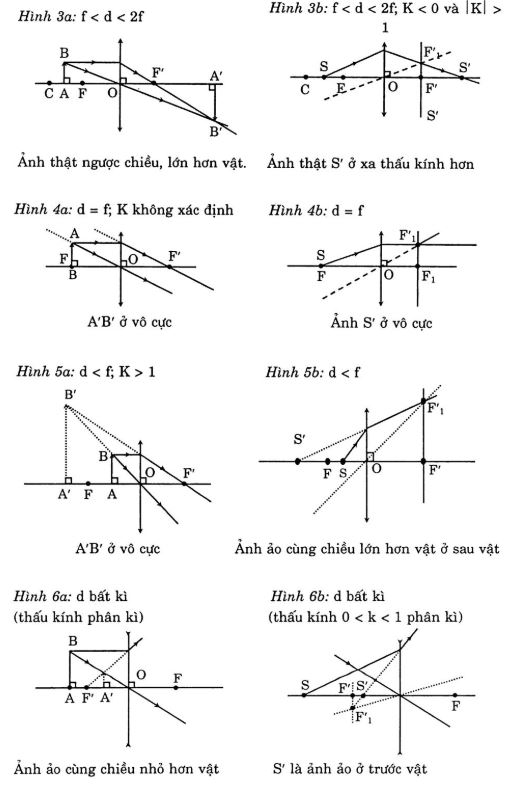
Xác định khoảng cách và vị trí ảnh

Để tính công thức khoảng cách ảnh thấu kính, ta cần xác định:

d’ = (d × f)/(d

• f)

Quy ước dấu:

• d’ dương: ảnh thật
• d’ âm: ảnh ảo
• f dương với thấu kính hội tụ
• f âm với thấu kính phân kỳ

Kinh nghiệm 20 năm giảng dạy cho thấy học sinh thường nhầm lẫn dấu. Cách tốt nhất là vẽ sơ đồ tia sáng trước khi áp dụng công thức.

Ứng dụng thực tiễn của công thức thấu kính mỏng

Công thức thấu kính mỏng có vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ. Công thức này giúp tính toán chính xác khoảng cách tiêu cự, độ phóng đại và vị trí của ảnh.

Trong các dụng cụ quang học

Các nhà sản xuất kính hiển vi sử dụng công thức này để thiết kế hệ thống thấu kính phức tạp. Việc tính toán chính xác giúp tạo ra hình ảnh phóng đại rõ nét.

Tôi thường giải thích cho học sinh rằng công thức lăng kính là gì có mối liên hệ mật thiết với thấu kính. Chúng đều tuân theo các nguyên lý quang học cơ bản.

Trong Công thức kính thiên văn, việc áp dụng công thức thấu kính mỏng giúp quan sát các thiên thể xa xôi một cách chi tiết và chính xác.

Trong thiết bị đo lường

Các thiết bị đo quang học như máy đo độ dày, máy đo khoảng cách laser đều ứng dụng nguyên lý thấu kính mỏng. Độ chính xác của phép đo phụ thuộc vào việc tính toán thông số thấu kính.

Qua 20 năm giảng dạy, tôi nhận thấy học sinh dễ hiểu nhất khi được thực hành với các thiết bị đo thực tế. Việc quan sát trực tiếp giúp các em nắm vững lý thuyết.

Trong y học và nghiên cứu

Ngành nhãn khoa sử dụng công thức này để thiết kế kính áp tròng và kính mắt. Các bác sĩ dựa vào đó để xác định độ cận, viễn của bệnh nhân một cách chính xác.

Trong phòng thí nghiệm, các nhà khoa học sử dụng hệ thống thấu kính để nghiên cứu vi sinh vật. Theo nghiên cứu của Viện Pasteur TP.HCM, độ phóng đại có thể đạt tới 1000 lần nhờ tổ hợp thấu kính được tính toán kỹ lưỡng.

Các kính hiển vi điện tử hiện đại còn cho phép quan sát cấu trúc phân tử, mở ra nhiều khả năng trong nghiên cứu sinh học và vật liệu.

FAQ: Câu hỏi thường gặp về công thức thấu kính mỏng

Trong quá trình giảng dạy, tôi nhận được rất nhiều câu hỏi về công thức thấu kính mỏng. Đây là những thắc mắc phổ biến nhất mà học sinh hay gặp phải.

• Công thức thấu kính mỏng có mấy dạng?

Có 2 dạng chính:

• Công thức thấu kính hội tụ: 1/f = 1/a + 1/a’
• Công thức thấu kính phân kỳ: 1/f = -1/a
  • 1/a’
• Làm sao phân biệt được dấu của tiêu cự f?

Thấu kính hội tụ có f > 0
Thấu kính phân kỳ có f < 0

• Công thức tính số phóng đại thấu kính là gì?

k = -a’/a = h’/h
Trong đó:

• k là độ phóng đại
• a’ là khoảng cách ảnh
• a là khoảng cách vật
• h’ là chiều cao ảnh
• h là chiều cao vật
• Khi nào ảnh là ảnh thật, ảnh ảo?

Ảnh thật khi a’ > 0
Ảnh ảo khi a’ < 0

• Tại sao gọi là thấu kính mỏng?

Vì bề dày của thấu kính nhỏ hơn nhiều so với bán kính cong của các mặt thấu kính.

Những câu hỏi trên giúp học sinh nắm vững kiến thức cơ bản về thấu kính mỏng và áp dụng công thức hiệu quả khi giải bài tập.

Việc áp dụng công thức thấu kính mỏng đóng vai trò quan trọng trong quang học và các ứng dụng thực tiễn. Các công thức tính toán về tiêu cự, độ tụ và số phóng đại giúp xác định chính xác đặc điểm của thấu kính hội tụ và phân kỳ. Những kiến thức này tạo nền tảng cho việc thiết kế, chế tạo các thiết bị quang học phục vụ đời sống và nghiên cứu khoa học.