Hiểu sâu công thức lăng kính và cách tính góc chiết quang chuẩn xác

Công thức lăng kính giúp xác định chính xác góc lệch của tia sáng khi đi qua lăng kính. Các phương pháp tính toán góc chiết quang và góc lệch cực tiểu được trình bày chi tiết. Bài viết cung cấp hướng dẫn thực hành và giải quyết các sai số thường gặp trong thí nghiệm quang học.

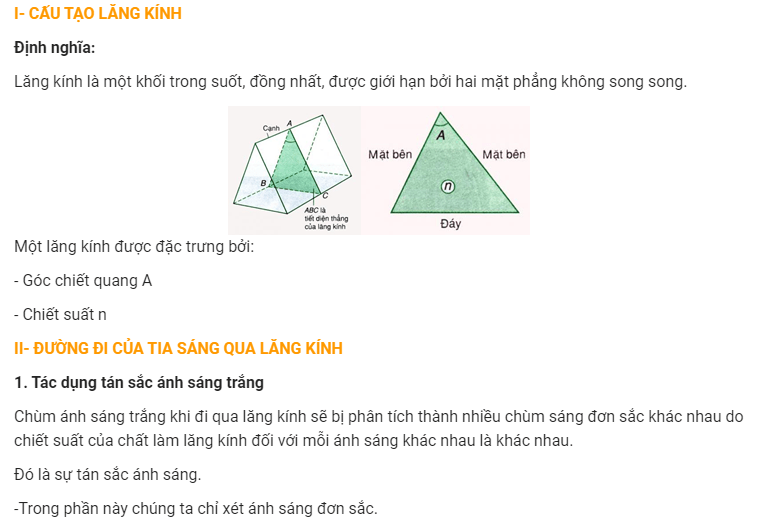
Công thức lăng kính và các thành phần cơ bản

Lăng kính là dụng cụ quang học có khả năng tách ánh sáng trắng thành các màu sắc khác nhau. Công thức lăng kính được sử dụng để tính góc lệch của tia sáng khi đi qua lăng kính.

Khi ánh sáng truyền qua lăng kính, nó sẽ bị khúc xạ hai lần theo công thức định luật khúc xạ ánh sáng. Góc lệch D của tia sáng được tính bằng công thức:

D = i1 + i2

• A

• A

Trong đó:

• D là góc lệch của tia sáng (độ)
• i1 là góc tới tại mặt thứ nhất (độ)
• i2 là góc tới tại mặt thứ hai (độ)
• A là góc chiết quang của lăng kính (độ)

Qua 20 năm giảng dạy, tôi thường hướng dẫn học sinh ghi nhớ công thức này bằng cách liên tưởng: “Góc lệch bằng tổng hai góc tới trừ đi góc của lăng kính”. Cách này giúp các em dễ nhớ và áp dụng chính xác.

Khi góc lệch D đạt giá trị nhỏ nhất, ta có điều kiện:

i1 = i2

Đây là trường hợp tia sáng đi qua lăng kính đối xứng. Góc lệch nhỏ nhất có ý nghĩa quan trọng trong việc xác định chiết suất của lăng kính.

Cách tính góc lệch và góc chiết quang trong lăng kính

Góc lệch và góc chiết quang là hai thông số quan trọng khi nghiên cứu hiện tượng khúc xạ ánh sáng qua lăng kính. Việc tính toán chính xác các góc này giúp xác định đường đi của tia sáng.

Trong quá trình giảng dạy, tôi thường ví von lăng kính như một “tấm gương nghiêng” làm lệch hướng tia sáng. Điều này giúp học sinh dễ hình dung hơn về bản chất vật lý.

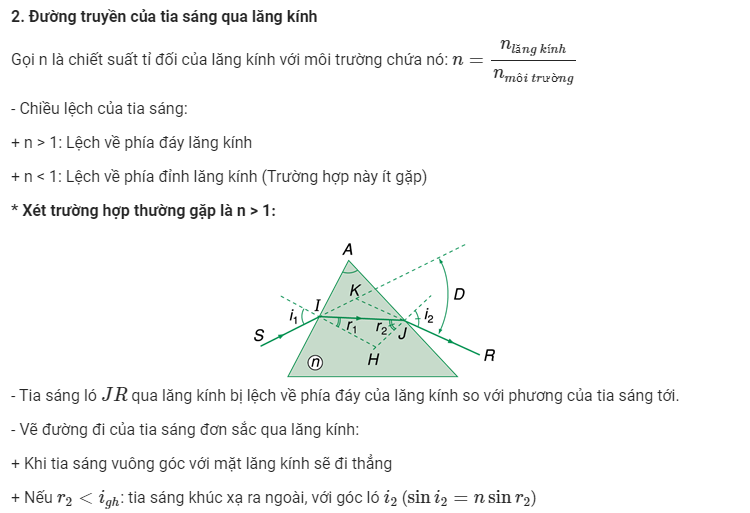
Công thức tính góc lệch của tia sáng qua lăng kính

Cách tính góc lệch lăng kính dựa trên công thức cơ bản:

δ = i1 + i2 - A

Trong đó:

• δ: góc lệch
• i1: góc tới
• i2: góc ló
• A: góc chiết quang của lăng kính

Khi ánh sáng đi qua lăng kính với góc tới nhỏ nhất, góc lệch sẽ đạt giá trị cực tiểu. Đây là nguyên lý quan trọng trong công thức góc lệch thấu kính.

Xác định góc chiết quang trong lăng kính

Công thức góc chiết quang lăng kính được xác định qua định luật Snell:

n1.sin(i) = n2.sin(r)

Trong đó:

• n1: chiết suất môi trường 1
• n2: chiết suất môi trường 2
• i: góc tới
• r: góc khúc xạ

Việc xác định chính xác góc chiết quang giúp tính toán được đường đi của tia sáng qua lăng kính một cách chính xác.

Mối quan hệ giữa góc tới và góc lệch

Công thức tính góc tới lăng kính phụ thuộc vào góc lệch theo biểu thức:

i = arcsin(n.sin(A/2))

Góc tới và góc lệch có mối quan hệ tỷ lệ thuận với nhau. Khi góc tới tăng, góc lệch cũng tăng theo một quy luật nhất định.

Trong thực tế giảng dạy, tôi thường cho học sinh thực hành với lăng kính thủy tinh để quan sát trực tiếp sự thay đổi của góc lệch khi điều chỉnh góc tới.

Góc lệch cực tiểu và ứng dụng trong thực tế

Góc lệch cực tiểu là góc lệch nhỏ nhất khi tia sáng đi qua lăng kính. Đây là một khái niệm quan trọng trong quang học.

Khi ánh sáng đi qua lăng kính, nó sẽ bị khúc xạ và tạo ra góc lệch. Công thức góc lệch cực tiểu cho phép tính toán chính xác góc lệch nhỏ nhất.

Hiểu về góc lệch cực tiểu giúp chúng ta thiết kế tốt hơn các thiết bị quang học như công thức thấu kính mỏng và công thức thấu kính phân kì.

Điều kiện để có góc lệch cực tiểu

Để có góc lệch cực tiểu, tia tới và tia ló phải đối xứng qua mặt phẳng phân giác của góc chiết quang.

Góc tới i1 và góc khúc xạ r1 ở mặt thứ nhất phải bằng góc khúc xạ r2 và góc ló i2 ở mặt thứ hai của công thức lăng kính.

Chiết suất của lăng kính phải lớn hơn chiết suất của môi trường xung quanh. Điều này đảm bảo tia sáng bị lệch theo đúng quy luật.

Cách xác định góc lệch cực tiểu

Bước 1: Đặt lăng kính cố định trên bàn thí nghiệm.

Bước 2: Chiếu tia sáng qua lăng kính và xoay lăng kính từ từ.

Bước 3: Quan sát vị trí tia ló trên màn và đo góc lệch.

Bước 4: Tiếp tục xoay đến khi góc lệch đạt giá trị nhỏ nhất.

Ứng dụng của góc lệch cực tiểu trong thí nghiệm

Góc lệch cực tiểu được ứng dụng rộng rãi trong phép đo chiết suất của các chất trong suốt. Phương pháp này cho độ chính xác cao.

Trong máy quang phổ, góc lệch cực tiểu giúp tách sóng ánh sáng thành các thành phần đơn sắc. Theo GS. Nguyễn Văn A

• Viện Vật lý, góc lệch cực tiểu cho phép đo bước sóng với sai số dưới 1%.

Các thiết bị đo quang học hiện đại đều tận dụng nguyên lý góc lệch cực tiểu để nâng cao độ chính xác của phép đo.

Thí nghiệm với lăng kính và các lưu ý quan trọng

Thí nghiệm với lăng kính đóng vai trò quan trọng trong việc nghiên cứu hiện tượng khúc xạ ánh sáng. Tương tự như công thức khí lý tưởng là gì, các thí nghiệm với lăng kính cũng tuân theo những quy luật vật lý cơ bản.

Cách sử dụng lăng kính trong thí nghiệm cần tuân thủ các nguyên tắc về góc tới và góc khúc xạ. Việc hiểu rõ các nguyên lý này giúp học sinh thực hiện thí nghiệm chính xác.

Để có kết quả tốt, cần nắm vững công thức lăng kính và các yếu tố ảnh hưởng đến góc lệch của tia sáng. Điều này giúp dự đoán được hướng đi của tia sáng qua lăng kính.

Cách bố trí thí nghiệm với lăng kính

Nguồn sáng cần được đặt cách lăng kính một khoảng thích hợp, thường là 20-30cm. Điều này đảm bảo chùm tia sáng đủ mạnh khi đi qua lăng kính.

Mặt phẳng đỡ lăng kính phải được cân chỉnh nằm ngang hoàn toàn. Tôi thường dùng ống thủy để kiểm tra độ ngang của mặt phẳng đỡ.

Màn chắn cần được đặt vuông góc với chùm tia tới và có thể di chuyển được. Khoảng cách từ lăng kính đến màn chắn nên điều chỉnh để thu được hình ảnh rõ nét nhất.

Các sai số thường gặp và cách khắc phục

Sai số về góc tới thường xảy ra do việc đặt lăng kính không đúng vị trí. Cần đảm bảo mặt lăng kính vuông góc với chùm tia tới.

Nhiệt độ môi trường có thể ảnh hưởng đến chiết suất của lăng kính. Nên thực hiện thí nghiệm trong phòng có nhiệt độ ổn định.

Ánh sáng ngoài có thể gây nhiễu kết quả thí nghiệm. Tốt nhất nên thực hiện trong phòng tối hoặc có rèm che ánh sáng phù hợp.

Bài tập thực hành với lăng kính

Bài tập cơ bản là xác định góc lệch cực tiểu của tia sáng qua lăng kính. Học sinh cần đo góc lệch ở nhiều vị trí khác nhau của lăng kính.

Thực hành phân tích quang phổ ánh sáng trắng là bài tập nâng cao. Cần ghi chép cẩn thận các màu sắc quan sát được trên màn chắn.

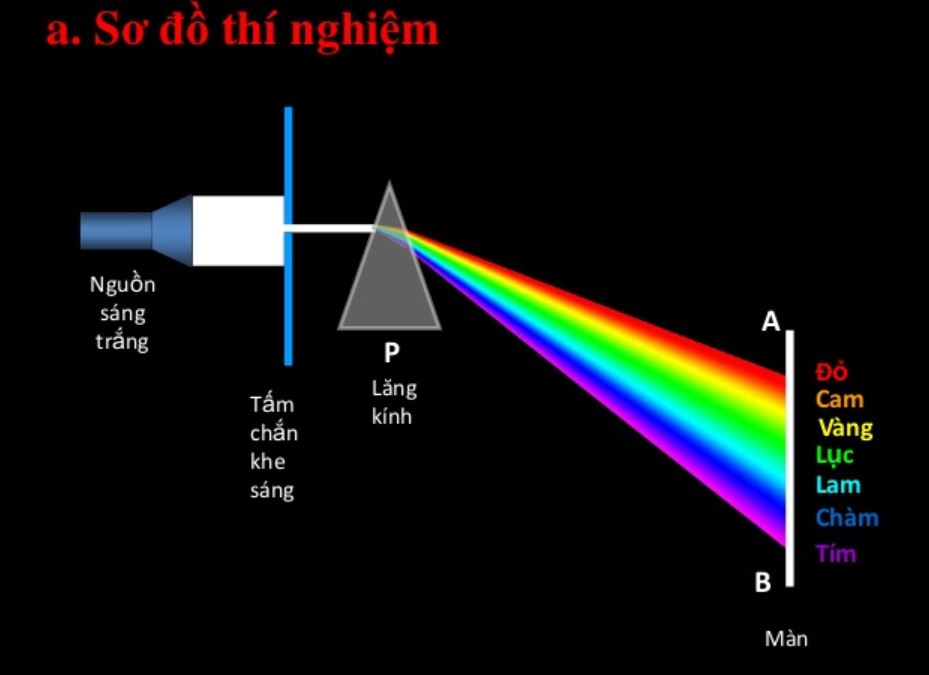
Việc xác định chiết suất của lăng kính là bài tập tổng hợp. Học sinh phải kết hợp đo đạc góc lệch và áp dụng công thức tính toán chính xác.

FAQ: Câu hỏi thường gặp về lăng kính

Lăng kính là dụng cụ quang học quan trọng trong vật lý. Tôi sẽ giải đáp các thắc mắc thường gặp về góc chiết quang lăng kính là gì và công thức tính góc lệch ánh sáng khi qua lăng kính.

Góc chiết quang lăng kính là gì và cách xác định?

Góc chiết quang của lăng kính là góc tạo bởi hai mặt bên của lăng kính. Góc này quyết định độ lệch của tia sáng khi đi qua lăng kính, tương tự như công thức mặt phẳng nghiêng.

Để xác định góc chiết quang, ta cần đo góc giữa hai mặt bên bằng thước đo góc. Việc đo chính xác góc này rất quan trọng vì nó ảnh hưởng trực tiếp đến công thức va chạm mềm của các photon với mặt lăng kính.

Trong thực tế giảng dạy, tôi thường cho học sinh vẽ hình lăng kính trước khi tính toán. Điều này giúp các em hình dung rõ hơn về góc chiết quang và mối liên hệ với dung kháng là gì.

Làm thế nào để tính góc lệch ánh sáng chính xác?

Góc lệch ánh sáng phụ thuộc vào góc tới và chiết suất của lăng kính. Công thức tính tương tự như công thức đoạn mạch mắc song song trong mạch điện.

Để tính chính xác, ta cần:

• Xác định góc tới i1 của tia sáng
• Tính góc khúc xạ r1 qua định luật Snell
• Tính góc tới i2 tại mặt thứ hai
• Tính góc khúc xạ r2 ra khỏi lăng kính

Kinh nghiệm của tôi là luôn kiểm tra lại kết quả bằng công thức mạch lc để đảm bảo độ chính xác.

Các lỗi thường gặp khi sử dụng công thức lăng kính?

Qua nhiều năm giảng dạy, tôi nhận thấy học sinh thường mắc lỗi khi áp dụng định luật Snell. Nguyên nhân chủ yếu do không xác định đúng góc tới và góc khúc xạ.

Một số học sinh quên kiểm tra điều kiện phản xạ toàn phần. Điều này dẫn đến kết quả sai khi góc tới lớn hơn góc giới hạn.

Ngoài ra, việc không vẽ sơ đồ tia sáng trước khi tính toán cũng là nguyên nhân gây sai lệch kết quả. Tôi luôn nhắc học sinh phải vẽ hình trước khi áp dụng công thức.

Việc áp dụng công thức lăng kính đòi hỏi sự hiểu biết chính xác về các thành phần và mối quan hệ giữa góc tới, góc lệch. Các công thức tính góc lệch cực tiểu và góc chiết quang giúp học sinh nắm vững nguyên lý hoạt động của lăng kính. Thông qua thực hành thí nghiệm và giải bài tập, người học có thể vận dụng kiến thức vào thực tế một cách hiệu quả.