Nắm rõ công thức độ biến thiên nội năng và cách tính trong vật lý
Công thức độ biến thiên nội năng giúp xác định sự thay đổi năng lượng bên trong vật chất. Các phương trình tính toán này áp dụng cho nhiều quá trình nhiệt động khác nhau. Bài viết trình bày chi tiết các công thức, phương pháp giải và bài tập thực hành phù hợp với mọi trình độ học tập.
Công thức độ biến thiên nội năng và ý nghĩa vật lý
Trong nhiệt động lực học, công thức độ biến thiên nội năng là một khái niệm quan trọng. Nó cho biết sự thay đổi năng lượng bên trong của hệ.
Công thức cơ bản được biểu diễn như sau:
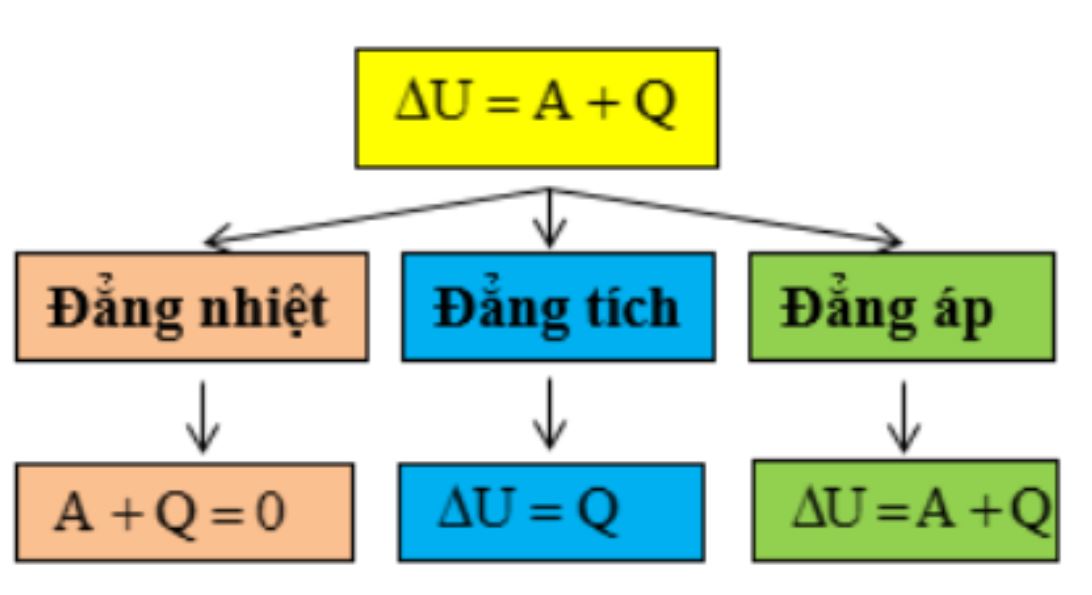
ΔU = Q + A
Trong đó:
- ΔU: độ biến thiên nội năng (J)
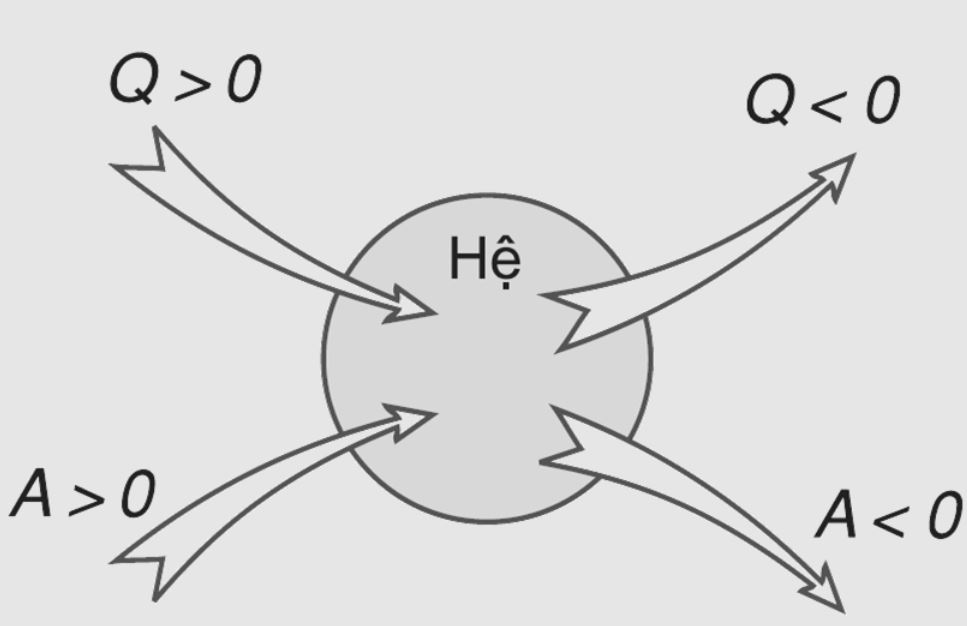
- Q: nhiệt lượng hệ nhận vào (+) hoặc tỏa ra (-)
- A: công ngoài tác dụng lên hệ (+) hoặc hệ sinh ra (-)
Khi giảng dạy, tôi thường ví von công thức này như “sổ thu chi” của một hệ nhiệt động. Nếu hệ nhận thêm năng lượng từ môi trường (Q>0, A>0), nội năng sẽ tăng. Ngược lại, khi hệ mất năng lượng ra môi trường (Q<0, A<0), nội năng giảm. Một ví dụ thực tế là khi bạn bơm xe đạp. Không khí trong bơm bị nén lại (A>0), đồng thời tỏa nhiệt ra môi trường (Q<0). Tổng của hai đại lượng này chính là độ biến thiên nội năng của khối khí.
Để áp dụng công thức hiệu quả, cần xác định rõ:
- Chiều của nhiệt lượng Q (nhận hay tỏa)
- Chiều của công A (tác dụng vào hay sinh ra)
- Quy ước dấu phù hợp (+/-)
Việc nắm vững công thức và ý nghĩa vật lý giúp giải quyết nhiều bài toán về biến đổi năng lượng trong các quá trình nhiệt động.
Khái niệm và bản chất của nội năng trong vật lý
Nội năng là tổng năng lượng của chuyển động nhiệt và tương tác giữa các phân tử trong vật. Đây là một đại lượng vật lý quan trọng trong nhiệt động lực học.
Khi nghiên cứu về nội năng, tôi thường ví von nó như “két sắt” chứa năng lượng bên trong vật. Két này luôn thay đổi khi vật tương tác với môi trường xung quanh.
Trong quá trình giảng dạy, tôi nhận thấy học sinh dễ nhầm lẫn nội năng với nhiệt độ. Nội năng phụ thuộc vào nhiều yếu tố, trong khi nhiệt độ chỉ đặc trưng cho mức độ chuyển động của phân tử.
Nội năng là gì và các thành phần cấu tạo
Nội năng bao gồm hai thành phần chính:
Động năng nhiệt: Là năng lượng chuyển động hỗn loạn của các phân tử.
Công thức: Ek = (3/2)kT
Trong đó:
- k là hằng số Boltzmann
- T là nhiệt độ tuyệt đối
Thế năng tương tác: Là năng lượng do lực tương tác giữa các phân tử.
Công thức: U = U0 + Ek
Trong đó U0 là thế năng tương tác giữa các phân tử
Sự biến đổi nội năng trong các quá trình nhiệt động
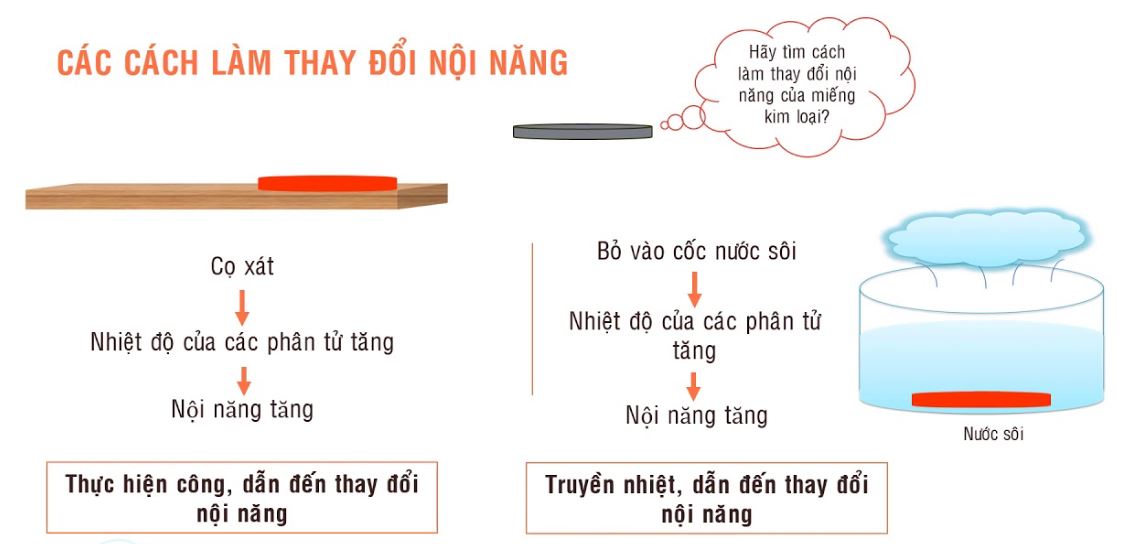
Nội năng có thể biến đổi theo hai cách:
Truyền nhiệt (Q): Khi có sự chênh lệch nhiệt độ giữa vật và môi trường.
Công thức: ΔU = Q (với quá trình đẳng tích)
Thực hiện công (A): Khi có lực tác dụng làm thay đổi thể tích vật.
Công thức: ΔU = -A (với quá trình đoạn nhiệt)
Định luật bảo toàn năng lượng cho ta:
ΔU = Q
Mối liên hệ giữa nội năng với nhiệt độ và áp suất
Nội năng tỷ lệ thuận với nhiệt độ tuyệt đối của vật. Khi nhiệt độ tăng, động năng nhiệt của phân tử tăng làm nội năng tăng.
Với khí lý tưởng, nội năng chỉ phụ thuộc vào nhiệt độ:
U = (3/2)nRT
Trong đó:
- n là số mol
- R là hằng số khí
- T là nhiệt độ tuyệt đối
Áp suất ảnh hưởng gián tiếp đến nội năng thông qua công thực hiện khi thay đổi thể tích. Tôi thường nhắc học sinh: “Áp suất như người gác cổng, quyết định năng lượng ra vào hệ”.
Các công thức tính độ biến thiên nội năng trong các quá trình đặc biệt
Độ biến thiên nội năng là đại lượng quan trọng trong nhiệt động lực học. Nó phụ thuộc vào nhiệt độ và thể tích của hệ.
Trong quá trình giảng dạy, tôi thường ví von nội năng như “tài khoản tiết kiệm” của hệ. Khi nhiệt độ tăng, “số dư” sẽ tăng lên.
Mối liên hệ giữa nội năng và công thức tính độ biến thiên động năng giúp ta hiểu rõ hơn về năng lượng của hệ.
Công thức tính ΔU trong quá trình đẳng tích
Trong quá trình đẳng tích, thể tích không đổi nên công cơ học bằng 0.
Công thức tính độ biến thiên nội năng trong đẳng tích:
ΔU = nCv(T2
Trong đó:
- n: Số mol chất khí
- Cv: Nhiệt dung riêng đẳng tích
- T2, T1: Nhiệt độ cuối và đầu
Công thức tính ΔU trong quá trình đẳng áp
Độ biến thiên nội năng trong đẳng áp được tính bằng công thức:
ΔU = nCv(T2 - T1)
Công thức này giống với đẳng tích vì nội năng chỉ phụ thuộc nhiệt độ. Tuy nhiên, trong đẳng áp có thêm công cơ học do thể tích thay đổi.
Kinh nghiệm của tôi là học sinh thường nhầm lẫn giữa Q và ΔU trong đẳng áp. Q = nCp(T2-T1) còn ΔU = nCv(T2-T1).
Công thức tính ΔU trong quá trình đẳng nhiệt
Trong quá trình đẳng nhiệt, nhiệt độ không đổi nên:
ΔU = 0
Đây là trường hợp đặc biệt vì nhiệt độ không thay đổi. Toàn bộ nhiệt lượng hệ nhận vào chuyển thành công cơ học.
Tôi thường giải thích cho học sinh bằng ví dụ: Giống như bạn rút tiền ra khỏi tài khoản (Q) và chi tiêu hết (A), số dư cuối cùng không đổi (ΔU = 0).
Phương pháp và bài tập áp dụng công thức độ biến thiên nội năng
Để tính toán chính xác cách tính độ biến thiên nội năng, chúng ta cần nắm vững các phương pháp và quy trình giải bài tập. Việc áp dụng công thức tính nội năng đúng cách sẽ giúp giải quyết các bài toán hiệu quả.
Trong quá trình giảng dạy 20 năm, tôi nhận thấy học sinh thường gặp khó khăn khi xác định dấu của công thức tính ΔU. Điều quan trọng là phải hiểu rõ quy ước dấu và các yếu tố ảnh hưởng.
Các bước giải bài tập về độ biến thiên nội năng
Bước 1: Xác định trạng thái đầu và cuối của hệ
- Ghi rõ các thông số nhiệt độ, áp suất, thể tích ban đầu và cuối cùng
- Xác định loại quá trình: đẳng nhiệt, đẳng tích hay đẳng áp
Bước 2: Áp dụng công thức phù hợp với từng quá trình
- Đẳng nhiệt: ΔU = 0
- Đẳng tích: ΔU = nCvΔT
- Đẳng áp: ΔU = nCvΔT
Bước 3: Thực hiện tính toán và kiểm tra kết quả
- Thay số và tính toán theo đơn vị SI
- Kiểm tra dấu của kết quả dựa trên quy ước
Bài tập mẫu và phương pháp giải chi tiết
Bài tập: Một khối khí lý tưởng thực hiện quá trình đẳng áp, nhiệt độ tăng từ 27°C lên 127°C. Tính độ biến thiên nội năng của khối khí, biết số mol n = 2 mol và Cv = 3R/2.
Giải:
ΔU = nCvΔT
= 2 × (3R/2) × (400
- 300)
Qua bài tập này, ta thấy việc chuyển đổi đơn vị nhiệt độ sang Kelvin rất quan trọng để có kết quả chính xác.
Một số lưu ý khi tính toán độ biến thiên nội năng

Khi giải các bài tập về nhiệt động lực học, cần đặc biệt chú ý đến đơn vị đo. Nhiệt độ phải được chuyển về thang Kelvin trước khi tính toán.
Quy ước dấu cũng rất quan trọng. Nếu hệ nhận nhiệt, nội năng tăng thì ΔU > 0. Ngược lại, khi hệ tỏa nhiệt, nội năng giảm thì ΔU < 0.
Với khí lý tưởng, nội năng chỉ phụ thuộc vào nhiệt độ. Do đó, trong quá trình đẳng nhiệt, độ biến thiên nội năng luôn bằng 0.
FAQ: Câu hỏi thường gặp về độ biến thiên nội năng
Độ biến thiên nội năng là một khái niệm quan trọng trong nhiệt động lực học. Tôi sẽ giải đáp các thắc mắc phổ biến về chủ đề này.
Mối quan hệ giữa độ biến thiên nội năng và nhiệt độ
Độ biến thiên nội năng có mối liên hệ trực tiếp với nhiệt độ của vật. Công thức tính nhiệt độ biến thiên phụ thuộc vào khối lượng và nhiệt dung riêng của vật.
Khi nhiệt độ tăng, động năng của các phân tử cũng tăng theo. Điều này dẫn đến sự gia tăng nội năng của hệ.
Trong quá trình giảng dạy, tôi thường lấy ví dụ về nước đun sôi. Khi đun nóng nước, nhiệt độ và nội năng của nước đều tăng lên.
Sự khác biệt giữa độ biến thiên nội năng và nhiệt lượng
Công thức tính nhiệt độ trong nội năng và nhiệt lượng có sự khác biệt cơ bản. Nội năng là năng lượng tổng của hệ.
Nhiệt lượng chỉ là một dạng truyền năng lượng. Nó có thể làm thay đổi nội năng của hệ.
Để hiểu rõ hơn, bạn có thể tham khảo thêm về công thức tính độ biến thiên từ thông để thấy sự tương đồng trong cách tiếp cận.
Ứng dụng của độ biến thiên nội năng trong thực tế
Độ biến thiên nội năng được ứng dụng rộng rãi trong công nghiệp nhiệt. Các nhà máy nhiệt điện sử dụng nguyên lý này.
Trong y tế, các thiết bị điều nhiệt cũng hoạt động dựa trên sự thay đổi nội năng. Máy điều hòa không khí là ví dụ điển hình.
Ngành công nghiệp thực phẩm cũng áp dụng nguyên lý này trong bảo quản, chế biến. Tủ lạnh hoạt động dựa trên sự biến thiên nội năng của môi chất lạnh.
Việc nắm vững công thức độ biến thiên nội năng giúp giải quyết các bài toán nhiệt động học một cách chính xác. Các công thức tính toán trong quá trình đẳng tích, đẳng áp và đẳng nhiệt tạo nền tảng cho việc phân tích các hiện tượng nhiệt. Kiến thức về nội năng và sự biến thiên của nó có ý nghĩa quan trọng trong nghiên cứu khoa học và ứng dụng thực tiễn.
Bài viết liên quan

Học công thức khí lý tưởng và các định luật cơ bản trong hóa học
Tìm hiểu công thức khí lý tưởng và các định luật liên quan qua phương pháp giảng dạy đơn giản. Bao gồm điều kiện, đặc điểm, bài tập mẫu và hướng dẫn giải chi tiết.

Học thuộc công thức tính nhiệt nóng chảy và ứng dụng trong hóa học
Tìm hiểu công thức tính nhiệt nóng chảy và các khái niệm cơ bản về nhiệt nóng chảy riêng, đơn vị đo, bảng tra cứu các chất thông dụng. Hướng dẫn chi tiết cách tính và ứng dụng thực tế.

Công thức đoạn nhiệt khái quát và cách áp dụng trong hóa học cơ bản
Tìm hiểu chi tiết về công thức đoạn nhiệt trong hóa học với cách tính, phương pháp xác định và ứng dụng. Bài viết giải thích đơn giản các khái niệm đoạn nhiệt chuẩn, phản ứng kèm bài tập mẫu.

Điểm qua công thức tính công suất tỏa nhiệt và ứng dụng thực tế
Tìm hiểu chi tiết công thức tính công suất tỏa nhiệt trong mạch điện với các khái niệm cơ bản, công thức Q=I²Rt và ứng dụng thực tế qua bài tập có lời giải mẫu đơn giản.

Nắm kỹ công thức tính nhiệt độ tuyệt đối và cách chuyển đổi thang nhiệt
Tìm hiểu công thức tính nhiệt độ tuyệt đối và cách chuyển đổi giữa độ C, K. Giải thích chi tiết khái niệm, ứng dụng thực tế cùng bài tập minh họa về thang nhiệt Kelvin.

Học công thức đẳng nhiệt và ứng dụng trong khí lý tưởng cơ bản
Tìm hiểu chi tiết công thức đẳng nhiệt và định luật Boyle-Mariotte qua các ví dụ, bài tập có lời giải. Phân tích đồ thị, ứng dụng thực tế giúp nắm vững kiến thức cơ bản.

