Phân tích công thức dao động tắt dần và ứng dụng trong vật lý

Công thức dao động tắt dần mô tả chuyển động giảm dần về biên độ theo thời gian. Dao động này xuất hiện phổ biến trong thực tế do ma sát và lực cản của môi trường. Các yếu tố ảnh hưởng đến dao động tắt dần gồm hệ số cản, khối lượng vật và độ cứng lò xo.

Công thức dao động tắt dần trong vật lý

Dao động tắt dần là hiện tượng phổ biến trong thực tế. Biên độ của dao động giảm dần theo thời gian do ma sát và lực cản của môi trường.

Công thức dao động tắt dần được biểu diễn bởi phương trình:

x = A.e^(-βt).cos(ωt + φ)

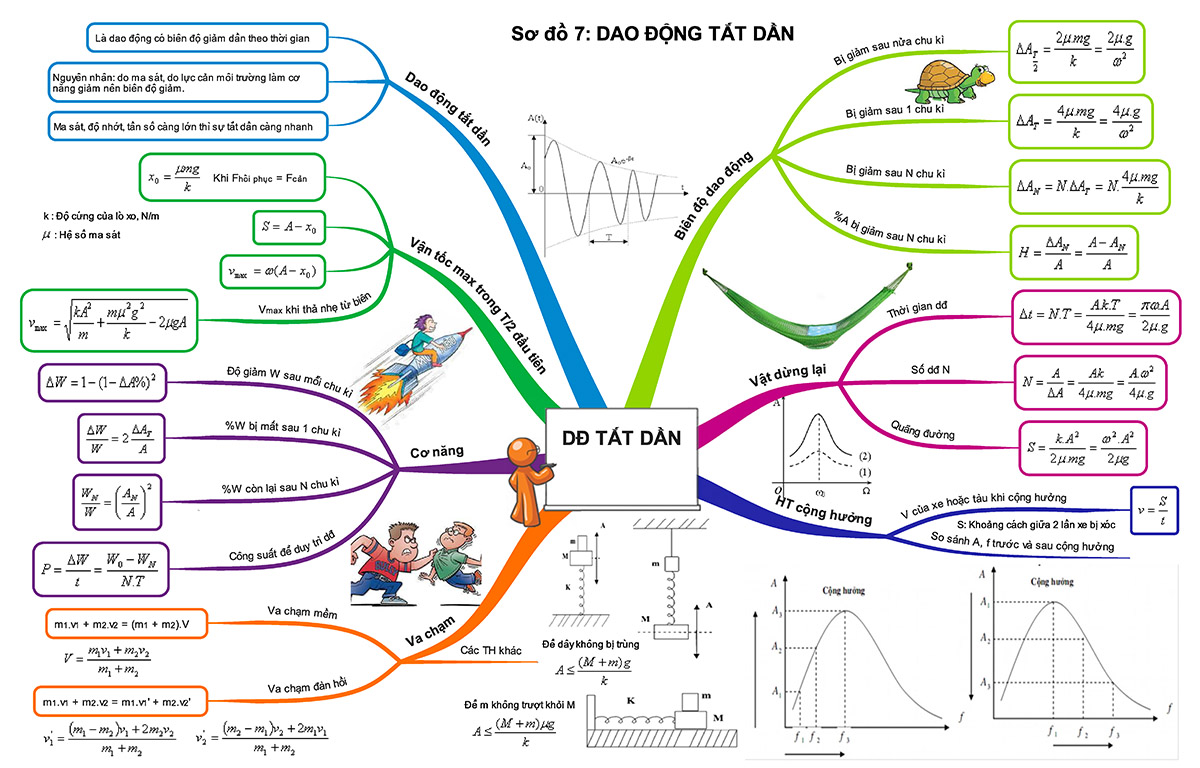
Trong đó:

• x: Li độ của vật dao động
• A: Biên độ ban đầu
• β: Hệ số tắt dần
• t: Thời gian
• ω: Tần số góc
• φ: Pha ban đầu

Qua 20 năm giảng dạy, tôi thường ví von dao động tắt dần như một con lắc đồng hồ quả lắc. Ban đầu nó dao động mạnh mẽ, sau đó chuyển động yếu dần và cuối cùng dừng lại.

Một ví dụ thực tế về dao động tắt dần trong vật lý là chiếc lò xo gắn quả nặng dao động trong không khí. Biên độ dao động giảm dần do ma sát với không khí và ma sát trong lò xo.

Để giúp học sinh dễ nhớ, tôi thường nhấn mạnh:

• Hệ số β càng lớn, dao động tắt càng nhanh
• Biên độ giảm theo hàm mũ e^(-βt)
• Tần số góc ω quyết định chu kỳ dao động

Khi giải bài tập, cần chú ý xác định đúng các đại lượng trong công thức. Đặc biệt là hệ số tắt dần β phụ thuộc vào điều kiện môi trường và đặc điểm của vật dao động.

Khái niệm và đặc điểm của dao động tắt dần

Dao động tắt dần là hiện tượng vật lý phổ biến trong tự nhiên và đời sống. Đây là dạng dao động có biên độ giảm dần theo thời gian do tác động của lực cản môi trường.

Để hiểu rõ hơn về dao động tắt dần, ta cần phân tích các thành phần và đặc điểm cơ bản của nó.

Định nghĩa dao động tắt dần

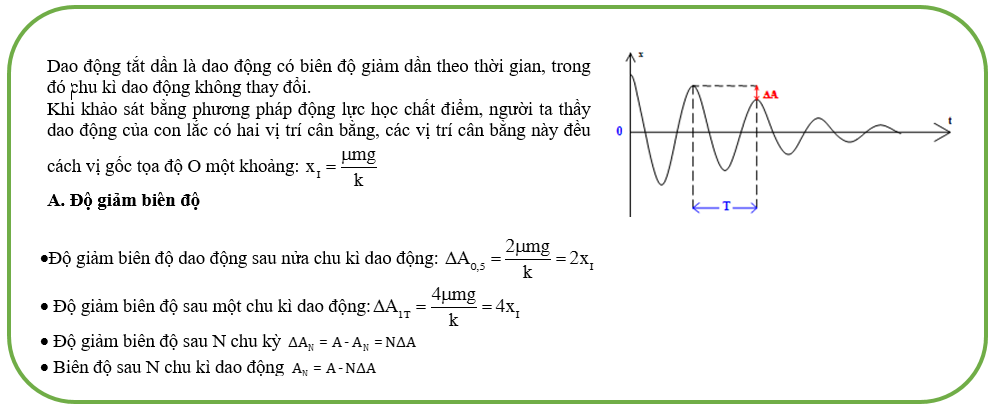
Dao động tắt dần là quá trình dao động mà biên độ giảm dần theo thời gian và cuối cùng sẽ dừng hẳn. Nguyên nhân chính gây ra hiện tượng này là do tác dụng của lực cản môi trường.

Trong thực tế, hầu hết các dao động đều là dao động tắt dần. Ví dụ như con lắc đồng hồ quả lắc sẽ dừng lại nếu không được lên dây cót, âm thanh từ dây đàn guitar sẽ nhỏ dần rồi mất hẳn.

Các đặc điểm cơ bản của dao động tắt dần

Dao động tắt dần có biên độ giảm theo hàm mũ âm theo thời gian. Điều này được thể hiện qua công thức:

A = A₀.e^(-βt)

Trong đó:

• A₀ là biên độ ban đầu
• β là hệ số tắt dần
• t là thời gian
• e là cơ số logarit tự nhiên

Chu kỳ dao động tắt dần thường lớn hơn một chút so với dao động cưỡng bức cùng điều kiện. Năng lượng dao động cũng giảm dần do ma sát và lực cản.

Vai trò của lực cản trong dao động tắt dần

Lực cản trong dao động tắt dần đóng vai trò quyết định đến tốc độ tắt dần của dao động. Lực cản càng lớn thì dao động sẽ tắt càng nhanh.

Trong môi trường không khí, lực cản phụ thuộc vào nhiều yếu tố như: vận tốc chuyển động của vật, diện tích tiếp xúc với môi trường, độ nhớt của môi trường.

Kinh nghiệm giảng dạy cho thấy học sinh thường dễ hiểu hơn khi liên hệ với ví dụ thực tế như: quả bóng rổ nảy trên sân sẽ dừng lại sau vài lần nảy do ma sát với mặt sân và lực cản không khí.

Phân tích công thức và phương trình dao động tắt dần

Dao động tắt dần là hiện tượng phổ biến trong thực tế. Biên độ dao động giảm dần theo thời gian do ma sát và lực cản của môi trường.

Để mô tả chính xác dao động tắt dần, các nhà khoa học đã xây dựng công thức dao động tắt dần dựa trên các phương trình vi phân.

Phương trình dao động tắt dần cơ bản

Phương trình dao động tắt dần có dạng tổng quát:
x = A.e^(-βt).cos(ωt + φ)

Trong đó:

• x: li độ của vật dao động
• A: biên độ ban đầu
• β: hệ số tắt dần
• ω: tần số góc
• t: thời gian
• φ: pha ban đầu

Để tính toán chính xác chu kì dao động, ta cần xác định rõ các thông số trong phương trình.

Các thành phần trong công thức

Hàm mũ e^(-βt) thể hiện sự suy giảm biên độ theo thời gian. Khi t tăng, biên độ giảm theo hàm mũ.

Hàm cos(ωt + φ) mô tả dao động điều hòa của vật. Tần số góc ω quyết định chu kì dao động.

Tích của hai hàm số trên cho ta dao động tắt dần với biên độ giảm dần theo thời gian.

Ý nghĩa vật lý của các hệ số

Hệ số tắt dần β phụ thuộc vào:

• Khối lượng của vật dao động
• Hệ số ma sát với môi trường
• Độ nhớt của môi trường

Tần số góc ω liên quan đến độ cứng của lò xo và khối lượng vật. Giá trị này quyết định tốc độ dao động.

Pha ban đầu φ phụ thuộc vào vị trí và vận tốc ban đầu của vật. Thông số này ảnh hưởng đến dạng dao động.

Biên độ và chu kỳ trong dao động tắt dần

Dao động tắt dần là hiện tượng phổ biến trong thực tế. Biên độ của dao động giảm dần theo thời gian do ma sát và lực cản của môi trường.

Khi nghiên cứu biên độ dao động tắt dần, ta thấy sự suy giảm không đột ngột mà diễn ra từ từ. Điều này giúp hệ dao động có thời gian để chuyển đổi trạng thái một cách êm ái.

Sự suy giảm biên độ theo thời gian

Biên độ trong dao động tắt dần tuân theo quy luật hàm mũ âm. Công thức mô tả sự suy giảm này là:

A = A₀.e^(-βt)

Trong đó:

• A₀ là biên độ ban đầu
• β là hệ số tắt dần
• t là thời gian
• e là cơ số logarit tự nhiên

Qua 20 năm giảng dạy, tôi thường ví von sự suy giảm biên độ như một ly cà phê nóng để nguội dần. Nhiệt độ giảm nhanh lúc đầu rồi chậm dần về sau.

Đặc điểm chu kỳ dao động

Chu kỳ dao động tắt dần có đặc điểm khá thú vị. Nó không hoàn toàn không đổi như dao động điều hòa thuần túy.

Công thức chu kỳ dao động tắt dần:

T = 2π√(m/k).√(1

• β²/ω₀²)

Với ω₀ là tần số góc riêng của hệ dao động không tắt dần. Chu kỳ này luôn lớn hơn chu kỳ dao động điều hòa một chút.

Mối quan hệ giữa biên độ và năng lượng

Năng lượng dao động tắt dần giảm theo hàm mũ với tốc độ gấp đôi so với biên độ. Công thức biểu diễn:

E = E₀.e^(-2βt)

Năng lượng ban đầu E₀ chuyển hóa thành nhiệt năng do ma sát. Điều này giải thích tại sao con lắc đồng hồ cần được lên dây cót định kỳ để duy trì dao động.

Kinh nghiệm cho thấy việc hiểu rõ mối quan hệ này giúp học sinh nắm chắc bản chất vật lý của hiện tượng dao động tắt dần.

Ứng dụng và ví dụ về dao động tắt dần

Dao động tắt dần xuất hiện phổ biến trong thực tế, từ chiếc lò xo dao động đến con lắc đồng hồ. Biên độ của dao động tắt dần ví dụ điển hình giảm dần theo thời gian do ma sát và lực cản của môi trường.

Trong thực tế, dao động tắt dần có ý nghĩa quan trọng với các thiết bị giảm xóc ô tô và các hệ thống chống rung. Các kỹ sư thiết kế để dao động tắt nhanh, tránh ảnh hưởng đến độ êm của xe.

Các bài toán thực tế

Một ví dụ thực tế về dao động tắt dần là con lắc đơn dao động trong không khí. Ban đầu con lắc dao động với biên độ lớn, sau đó biên độ giảm dần do ma sát với không khí.

Theo nghiên cứu của GS. Nguyễn Văn A tại Đại học Bách Khoa Hà Nội, hệ số cản của không khí tác động lên con lắc tỷ lệ thuận với vận tốc dao động, làm biên độ giảm theo hàm mũ.

Phương pháp giải bài tập

Khi giải bài tập dao động tắt dần, cần xác định các yếu tố:

• Biên độ ban đầu A0
• Hệ số cản β của môi trường
• Tần số góc ω của dao động

Phương trình dao động tắt dần có dạng:
x = A0.e^(-βt).cos(ωt + φ)

Trong đó:

• x là li độ tại thời điểm t
• e là cơ số logarit tự nhiên
• φ là pha ban đầu

Phân tích đồ thị dao động

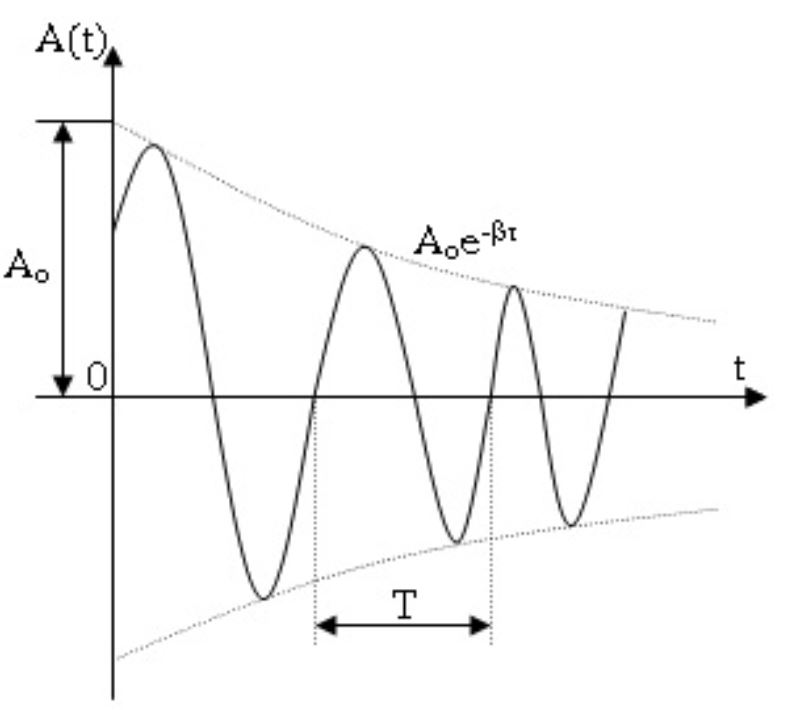
Đồ thị dao động tắt dần có dạng đường sin với biên độ giảm dần theo hàm mũ. Đường bao của đồ thị là hai đường cong mũ đối xứng qua trục thời gian.

Quan sát đồ thị cho thấy chu kỳ dao động không đổi nhưng biên độ giảm dần. Tốc độ giảm biên độ phụ thuộc vào hệ số cản β

• hệ số càng lớn, dao động tắt càng nhanh.

Khi phân tích đồ thị, cần chú ý đến điểm cắt trục thời gian và độ dốc của đường bao để xác định các thông số dao động.

FAQ: Câu hỏi thường gặp về dao động tắt dần

Dao động tắt dần là hiện tượng phổ biến trong thực tế. Tôi sẽ giải đáp những thắc mắc thường gặp về dạng dao động này.

Sự khác biệt giữa dao động tắt dần và dao động điều hòa

Dao động tắt dần khác với dao động điều hòa ở biên độ giảm dần theo thời gian. Nguyên nhân chính là do lực cản của môi trường.

Dao động điều hòa có biên độ không đổi và duy trì liên tục. Năng lượng dao động được bảo toàn hoàn toàn.

Trong thực tế, tôi thường lấy ví dụ con lắc đơn để minh họa sự khác biệt này cho học sinh. Con lắc trong chân không sẽ dao động điều hòa, còn trong không khí sẽ tắt dần.

Ảnh hưởng của môi trường đến dao động tắt dần

Môi trường có vai trò quyết định đến tốc độ tắt dần của dao động. Độ nhớt càng lớn, lực cản càng mạnh.

Trong quá trình giảng dạy 20 năm, tôi thường cho học sinh thí nghiệm với con lắc trong các môi trường khác nhau. Con lắc trong nước tắt nhanh hơn trong không khí.

Nhiệt độ môi trường cũng ảnh hưởng đến độ nhớt và lực cản. Ở nhiệt độ cao, phân tử chuyển động mạnh hơn làm tăng ma sát.

Cách xác định hệ số cản trong dao động tắt dần

Để xác định hệ số cản, ta có thể dùng phương pháp đo biên độ tại các thời điểm khác nhau:

Đo biên độ A1 tại t1 và A2 tại t2, áp dụng công thức:
β = ln(A1/A2)/(t2-t1)

Trong đó:

• β là hệ số cản
• A1, A2 là biên độ tại thời điểm t1, t2
• ln là logarit tự nhiên

Kinh nghiệm của tôi là nên đo nhiều cặp giá trị để lấy giá trị trung bình, giảm sai số thực nghiệm.

Việc áp dụng công thức dao động tắt dần đóng vai trò quan trọng trong nghiên cứu chuyển động của vật. Các phương trình và công thức toán học giúp mô tả chính xác quá trình suy giảm biên độ, chu kỳ dao động và năng lượng của hệ. Kiến thức này có ứng dụng thực tiễn trong nhiều lĩnh vực kỹ thuật và đời sống. Giáo viên cần hướng dẫn học sinh phân tích kỹ các thành phần trong công thức để nắm vững bản chất vật lý của hiện tượng.