Công thức sóng cơ và các đại lượng đặc trưng trong vật lý
Công thức sóng cơ giúp mô tả chính xác các hiện tượng dao động trong tự nhiên. Các đại lượng đặc trưng như bước sóng, chu kỳ và tần số có mối liên hệ mật thiết với nhau. Sóng cơ đóng vai trò quan trọng trong âm nhạc, y học và công nghiệp hiện đại.
Công thức sóng cơ và các thành phần cơ bản
Khi nghiên cứu về công thức sóng cơ, chúng ta cần nắm vững các thành phần cơ bản. Tôi sẽ giải thích chi tiết từng phần để các em dễ hiểu nhất.
Công thức sóng được biểu diễn qua phương trình dao động:
y = A.cos(ωt
Trong đó:
- y: Li độ dao động (m)
- A: Biên độ sóng (m)
- ω: Tần số góc (rad/s)
- t: Thời gian (s)
- k: Số sóng (rad/m)
- φ: Pha ban đầu (rad)
Qua 20 năm giảng dạy, tôi thường chia nhỏ công thức thành 2 phần để học sinh dễ nhớ:
- Phần biên độ A thể hiện độ lớn dao động
- Phần pha [cos(ωt
- kx + φ)] thể hiện trạng thái dao động
Một mẹo nhỏ khi giải bài tập: Các em cần xác định rõ các đại lượng đã cho và cần tìm. Sau đó thay số vào từng thành phần của công thức.
Ví dụ: Một sóng có biên độ 2cm, tần số 50Hz, bước sóng 10cm. Tính vận tốc truyền sóng.
Áp dụng công thức: v = λ.f

v = 0,1m × 50Hz = 5m/s
Như vậy, việc nắm vững các thành phần trong công thức sẽ giúp các em giải được nhiều dạng bài tập khác nhau.
Phân loại sóng cơ và đặc điểm của từng loại
Sóng cơ là dạng dao động lan truyền trong môi trường vật chất. Chúng được phân thành nhiều loại khác nhau dựa trên phương dao động và đặc điểm truyền sóng.
Mỗi loại sóng cơ có những tính chất riêng biệt và ứng dụng trong thực tế. Việc phân loại giúp ta hiểu rõ bản chất và cách thức lan truyền của từng loại sóng.
Sóng ngang và đặc điểm truyền sóng
Sóng ngang là hiện tượng dao động của các phần tử môi trường theo phương vuông góc với phương truyền sóng. Đây là dạng sóng phổ biến trong tự nhiên.
Khi quan sát một sợi dây đàn guitar, ta thấy các điểm trên dây dao động lên xuống trong khi sóng truyền từ trái sang phải. Đó chính là đặc trưng của sóng ngang.
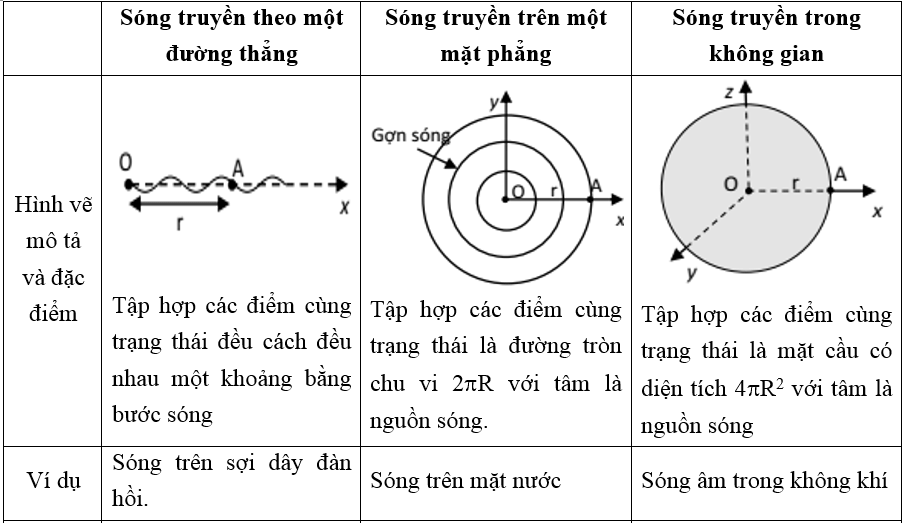
Sóng ngang thường xuất hiện trong các môi trường rắn như dây đàn, mặt nước và có liên quan mật thiết đến công thức va chạm mềm khi nghiên cứu va đập.
Sóng dọc và cách lan truyền
Sóng dọc là dạng sóng có phương dao động của các phần tử môi trường trùng với phương truyền sóng. Chúng tạo ra các vùng dãn nở và nén ép liên tiếp.
Một ví dụ điển hình là lò xo dao động. Khi kéo một đầu lò xo, các vòng xoắn sẽ co giãn theo chiều dọc trục lò xo.
Trong không khí, sóng dọc tạo ra các vùng không khí có mật độ khác nhau, giúp âm thanh truyền đi xa.
Sóng dừng và điều kiện hình thành
Sóng dừng là hiện tượng giao thoa giữa hai sóng có cùng tần số và biên độ truyền ngược chiều nhau. Chúng tạo ra các điểm nút và bụng cố định.
Điều kiện để hình thành sóng dừng là hai đầu của môi trường phải được cố định hoặc tự do. Ví dụ như dây đàn guitar khi được gảy.
Trong phòng thí nghiệm, tôi thường cho học sinh quan sát sóng dừng trên dây đàn hồi để hiểu rõ hơn về hiện tượng này.
Sóng âm và đặc tính vật lý
Sóng âm là dạng sóng cơ học lan truyền trong môi trường vật chất dưới dạng sóng dọc. Chúng mang năng lượng và thông tin âm thanh.
Tai người chỉ có thể nghe được sóng âm có tần số từ 20Hz đến 20.000Hz. Đây là dải tần số âm thanh mà con người có thể cảm nhận được.
Trong y học, sóng siêu âm với tần số trên 20.000Hz được ứng dụng rộng rãi trong chẩn đoán và điều trị bệnh.
Các đại lượng đặc trưng và công thức tính toán sóng cơ
Sóng cơ là hiện tượng lan truyền dao động trong môi trường vật chất. Công thức sóng cơ giúp mô tả các đặc trưng cơ bản của sóng như bước sóng, chu kỳ, tần số và vận tốc.
Bước sóng và phương pháp xác định
Công thức tính bước sóng được biểu diễn qua công thức:
λ = v.T = v/f
Trong đó:
- λ là bước sóng (m)
- v là vận tốc truyền sóng (m/s)
- T là chu kỳ dao động (s)
- f là tần số dao động (Hz)
Qua 20 năm giảng dạy, tôi thường hướng dẫn học sinh xác định bước sóng bằng cách đo khoảng cách giữa hai điểm gần nhất dao động cùng pha trên phương truyền sóng.
Chu kỳ sóng và ứng dụng thực tế
Công thức tính chu kỳ sóng là:
T = 1/f = λ/v
Trong đó T là chu kỳ dao động (s).
Chu kỳ sóng có ứng dụng quan trọng trong nhiều lĩnh vực. Ví dụ trong y học, sóng siêu âm với chu kỳ dao động phù hợp được dùng để chẩn đoán bệnh.
Trong công nghiệp, chu kỳ sóng âm được kiểm soát để tạo ra các thiết bị siêu âm làm sạch chính xác.
Tần số sóng và mối quan hệ với chu kỳ
Công thức tính tần số sóng được biểu diễn:
f = 1/T = v/λ
Trong đó f là tần số dao động (Hz).
Tần số và chu kỳ có mối quan hệ nghịch đảo. Khi tần số tăng thì chu kỳ giảm và ngược lại.
Kinh nghiệm cho thấy học sinh thường nhớ tốt hơn khi liên hệ với âm nhạc
- tần số càng cao thì âm thanh càng cao và ngược lại.
Vận tốc sóng và các yếu tố ảnh hưởng
Công thức tính vận tốc sóng là:
v = λ.f = λ/T

Trong đó v là vận tốc truyền sóng (m/s).
Vận tốc sóng phụ thuộc vào đặc tính của môi trường truyền sóng như công thức chuyển động thẳng đều là gì.
Trong môi trường đàn hồi, vận tốc sóng tăng khi độ đàn hồi tăng và giảm khi khối lượng riêng của môi trường tăng.
Ứng dụng của sóng cơ trong thực tế và kỹ thuật
Sóng cơ đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống và công nghệ. Các ứng dụng của sóng cơ ngày càng được mở rộng nhờ sự phát triển của khoa học kỹ thuật.
Việc nghiên cứu và ứng dụng sóng cơ giúp con người tạo ra nhiều thiết bị và công nghệ hữu ích. Từ âm nhạc, y tế cho đến công nghiệp đều có sự hiện diện của sóng cơ.
Sóng cơ trong âm nhạc và âm thanh
Âm nhạc là một trong những ứng dụng phổ biến nhất của sóng cơ. Các nhạc cụ tạo ra âm thanh thông qua dao động của dây đàn hoặc màng rung.

Tương tự như công thức mạch dao động, các dây đàn dao động với tần số xác định tạo ra các nốt nhạc. Độ căng của dây đàn quyết định cao độ của âm thanh phát ra.
Trong phòng thu âm, người ta thiết kế các vật liệu hấp thụ và phản xạ âm thanh. Điều này giúp tạo ra chất lượng âm thanh tốt nhất cho các bản thu.
Sóng cơ trong y học và chẩn đoán
Siêu âm là công nghệ chẩn đoán hình ảnh dựa trên nguyên lý truyền sóng cơ. Sóng siêu âm có tần số cao hơn giới hạn nghe của tai người.
Khi sóng siêu âm truyền qua các mô trong cơ thể, chúng bị phản xạ với mức độ khác nhau. Máy tính xử lý các tín hiệu phản xạ để tạo ra hình ảnh chi tiết của các cơ quan nội tạng.
Công nghệ này an toàn và không xâm lấn nên được sử dụng rộng rãi. Đặc biệt trong theo dõi thai nhi và chẩn đoán các bệnh lý về tim mạch.
Sóng cơ trong công nghiệp và xây dựng
Ngành công nghiệp sử dụng sóng cơ trong nhiều ứng dụng khác nhau. Tương tự như công thức máy phát điện xoay chiều, sóng cơ giúp chuyển đổi năng lượng cơ học thành điện năng.
Trong xây dựng, kỹ sư sử dụng sóng cơ để kiểm tra độ bền của công trình. Các thiết bị đo dao động giúp phát hiện các vết nứt hoặc khuyết tật trong kết cấu.
Công nghệ rung động còn được ứng dụng trong sàng lọc, phân loại vật liệu. Các máy sàng rung tạo ra dao động có tần số phù hợp để tách các hạt có kích thước khác nhau.
FAQ: Câu hỏi thường gặp về sóng cơ
Sóng cơ là một hiện tượng vật lý phổ biến trong tự nhiên. Tôi sẽ giải đáp một số thắc mắc thường gặp về chủ đề này.
- Sóng cơ có tuân theo định luật bảo toàn năng lượng không?
Sóng cơ tuân theo công thức bảo toàn cơ năng như mọi chuyển động cơ học khác. Năng lượng sóng được bảo toàn khi không có tổn hao.
- Dung kháng trong sóng âm là gì?
Đơn vị dung kháng đặc trưng cho khả năng cản trở dao động của môi trường. Nó phụ thuộc vào mật độ và tốc độ truyền sóng.
- Làm sao tính tổng trở khi có nhiều sóng giao thoa?
Công thức tính tổng trở của mạch giúp xác định tổng trở kháng khi có nhiều sóng. Đây là yếu tố quan trọng trong âm học.
- Sóng cơ truyền qua các môi trường khác nhau như thế nào?
Khi truyền qua các môi trường, sóng tuân theo công thức mạch song song. Biên độ và tần số có thể thay đổi tùy môi trường.
Kiến thức về công thức sóng cơ giúp người học nắm vững các khái niệm cơ bản và ứng dụng trong thực tiễn. Các công thức tính toán đơn giản cùng với sự phân loại rõ ràng tạo nền tảng cho việc học tập và nghiên cứu sâu hơn. Sóng cơ đóng vai trò quan trọng trong nhiều lĩnh vực như âm nhạc, y học và công nghiệp hiện đại.
Bài viết liên quan

Phân tích công thức dao động tắt dần và ứng dụng trong vật lý
Tìm hiểu chi tiết công thức dao động tắt dần qua các khái niệm, đặc điểm và ứng dụng thực tế. Phân tích phương trình, biên độ, chu kỳ cùng các bài tập minh họa dễ hiểu.

Công thức dao động điện từ và các ứng dụng trong mạch LC cơ bản
Tìm hiểu công thức dao động điện từ trong mạch LC với các yếu tố cơ bản, năng lượng, chu kỳ và ứng dụng thực tế. Giải thích chi tiết cho học sinh dễ hiểu.

Tìm hiểu công thức tính li độ cực đại và ứng dụng trong dao động điều hòa
Tìm hiểu công thức tính li độ cực đại trong dao động điều hòa, mối quan hệ với biên độ và các đại lượng vật lý. Hướng dẫn chi tiết cách xác định qua đồ thị và bài tập.

Thuộc lòng công thức tính chiều dài quỹ đạo và các đường cong cơ bản
Tìm hiểu công thức tính chiều dài quỹ đạo cho chuyển động tròn, elip và các đường cong. Hướng dẫn chi tiết cách áp dụng công thức với bài tập từ cơ bản đến nâng cao.

Nắm rõ công thức dao động cơ và các dạng dao động điều hòa cơ bản
Tìm hiểu công thức dao động cơ qua các khái niệm cơ bản về dao động điều hòa, tắt dần và cưỡng bức. Phân tích chi tiết biên độ, tần số, chu kỳ và pha dao động trong vật lý phổ thông.

Tổng quan công thức tính vận tốc góc và ứng dụng trong vật lý
Tìm hiểu công thức tính vận tốc góc và cách áp dụng trong chuyển động tròn đều. Giải thích chi tiết khái niệm, đơn vị đo và mối quan hệ với vận tốc dài kèm bài tập minh họa.

