Điểm qua công thức tính cơ năng của con lắc đơn và các ứng dụng thực tế

Công thức tính cơ năng của con lắc đơn giúp xác định năng lượng cơ học của vật dao động. Con lắc đơn chuyển đổi qua lại giữa thế năng và động năng trong quá trình dao động. Các yếu tố như khối lượng, chiều dài dây và góc lệch ảnh hưởng trực tiếp đến cơ năng của hệ.

Công thức tính cơ năng của con lắc đơn

Con lắc đơn là một hệ dao động cơ học phổ biến trong vật lý. Khi con lắc dao động, năng lượng của nó được bảo toàn và chuyển đổi qua lại giữa động năng và thế năng.

Công thức tính cơ năng của con lắc đơn được xác định bằng tổng của động năng và thế năng tại mọi thời điểm:

E = Ek + Ep = 1/2mv² + mgh

Trong đó:

• E: Cơ năng của con lắc (J)
• Ek: Động năng (J)
• Ep: Thế năng (J)
• m: Khối lượng vật nặng (kg)
• v: Vận tốc tức thời (m/s)
• g: Gia tốc trọng trường (m/s²)
• h: Độ cao so với vị trí cân bằng (m)

Qua 20 năm giảng dạy, tôi thường gợi ý học sinh hình dung con lắc như một đứa trẻ đang chơi xích đu. Khi ở điểm cao nhất, thế năng đạt cực đại và động năng bằng 0. Ngược lại tại vị trí cân bằng, động năng đạt cực đại và thế năng bằng 0.

Một điểm quan trọng cần nhớ là cơ năng luôn được bảo toàn trong điều kiện lý tưởng. Điều này có nghĩa tổng của động năng và thế năng tại mọi thời điểm đều bằng nhau và bằng cơ năng ban đầu của hệ.

Tìm hiểu về con lắc đơn và các thành phần cơ bản

Con lắc đơn là một trong những hệ dao động cơ học đơn giản và quan trọng trong vật lý. Nó giúp chúng ta hiểu được các nguyên lý cơ bản về dao động điều hòa và ứng dụng trong thực tế.

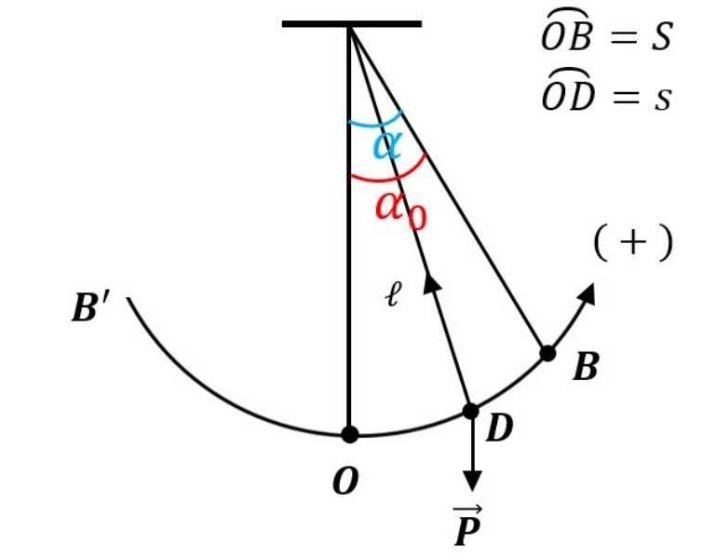
Con lắc đơn là gì và cấu tạo

Con lắc đơn là một hệ gồm vật nặng được treo vào một đầu dây không giãn, đầu còn lại được gắn cố định. Khi vật nặng được kéo lệch khỏi vị trí cân bằng rồi thả ra, nó sẽ dao động quanh vị trí đó.

Cấu tạo của con lắc đơn bao gồm một sợi dây có chiều dài L và một quả cầu khối lượng m. Sợi dây được coi là không có khối lượng và không giãn trong quá trình dao động.

Các đại lượng đặc trưng của con lắc đơn

Chu kỳ dao động (T) là thời gian để con lắc thực hiện một dao động toàn phần. Công thức tính chu kỳ:

T = 2π√(L/g)

Trong đó:

• L là chiều dài dây treo (m)
• g là gia tốc trọng trường (m/s²)
• π ≈ 3,14

Tần số dao động (f) là số dao động toàn phần trong 1 giây:

f = 1/T = 1/(2π√(L/g))

Dao động của con lắc đơn

Dao động con lắc đơn là dao động điều hòa khi biên độ góc nhỏ (α ≤ 10°). Lực kéo về trong dao động này là hợp lực của trọng lực và lực căng dây.

Phương trình dao động của con lắc:

α = α₀cos(ωt + φ)

Trong đó:

• α là li độ góc tại thời điểm t
• α₀ là biên độ góc
• ω là tần số góc (ω = 2π/T)
• φ là pha ban đầu

Kinh nghiệm giảng dạy cho thấy học sinh thường nhớ tốt hơn khi liên hệ với thực tế như đồng hồ quả lắc hoặc trò chơi xích đu.

Phân tích chi tiết công thức cơ năng con lắc đơn

Công thức cơ năng con lắc đơn là tổng của thế năng và động năng tại mỗi thời điểm. Đây là một hằng số không đổi khi bỏ qua ma sát.

Để hiểu rõ cơ năng của con lắc, ta cần phân tích từng thành phần năng lượng riêng biệt. Mỗi dạng năng lượng đều có vai trò quan trọng trong chuyển động của con lắc.

Thế năng của con lắc đơn

Công thức thế năng con lắc đơn được xác định bởi:

Ep = mgh = mgl(1-cosα)

Trong đó:

• m là khối lượng vật (kg)
• g là gia tốc trọng trường (m/s2)
• h là độ cao so với vị trí thấp nhất (m)
• l là chiều dài dây (m)
• α là góc lệch với phương thẳng đứng (rad)

Thế năng đạt giá trị lớn nhất khi con lắc ở vị trí biên, nơi góc lệch α đạt cực đại. Ngược lại, thế năng bằng 0 tại vị trí thấp nhất.

Động năng của con lắc đơn

Động năng của con lắc được tính theo công thức:

Ek = 1/2mv2

Trong đó:

• m là khối lượng vật (kg)
• v là vận tốc tức thời của vật (m/s)

Động năng đạt cực đại khi con lắc đi qua vị trí cân bằng, nơi vận tốc lớn nhất. Tại vị trí biên, động năng bằng 0.

Tổng cơ năng con lắc đơn

Năng lượng con lắc đơn được bảo toàn theo công thức:

E = Ep + Ek = hằng số

Khi bỏ qua ma sát, công thức tính cơ năng của con lắc đơn là:

E = mgl(1-cosα0)

Với α0 là biên độ dao động ban đầu. Đây là một đại lượng không đổi trong suốt quá trình dao động của con lắc.

Trong thực tế giảng dạy, tôi thường nhấn mạnh với học sinh rằng năng lượng chỉ chuyển hóa qua lại giữa thế năng và động năng mà không mất đi.

Các công thức quan trọng liên quan đến con lắc đơn

Con lắc đơn là một hệ dao động cơ học đơn giản và phổ biến trong vật lý. Việc nắm vững các công thức con lắc đơn giúp giải quyết nhiều bài toán thực tế.

Tôi thường ví von con lắc đơn như một người đang đung đưa trên xích đu. Chuyển động này tuân theo các quy luật vật lý chặt chẽ và có thể tính toán chính xác.

Công thức tính chu kỳ dao động

Cách tính chu kỳ con lắc đơn được thể hiện qua công thức:

T = 2π√(l/g)

Trong đó:

• T là chu kỳ dao động (s)
• l là chiều dài dây treo (m)
• g là gia tốc trọng trường (m/s²)

Kinh nghiệm giảng dạy cho thấy học sinh thường nhầm lẫn giữa l và g. Tôi thường nhắc các em nhớ “l” là “length”

• chiều dài dây treo.

Công thức tính tần số dao động

Tần số con lắc đơn được tính bằng nghịch đảo của chu kỳ:

f = 1/T = 1/(2π)√(g/l)

Trong đó f là tần số dao động (Hz).

Để học sinh dễ nhớ, tôi thường liên hệ với công thức tính thế năng con lắc lò xo có cùng dạng nghịch đảo.

Công thức tính biên độ dao động

Biên độ con lắc đơn phụ thuộc vào góc lệch ban đầu α₀:

A = l.sin(α₀)

Trong đó:

• A là biên độ dao động (m)
• α₀ là góc lệch ban đầu (rad)

Lưu ý quan trọng: Công thức chỉ đúng với góc lệch nhỏ (α₀ ≤ 10°). Với góc lớn hơn cần áp dụng các phương pháp tính toán phức tạp hơn.

Ứng dụng của con lắc đơn trong thực tế

Con lắc đơn với công thức tính cơ năng của con lắc đơn đã mở ra nhiều ứng dụng quan trọng. Các ứng dụng này dựa trên nguyên lý dao động điều hòa và tính tuần hoàn của con lắc.

Ứng dụng trong đồng hồ quả lắc

Đồng hồ quả lắc là một trong những ứng dụng con lắc đơn phổ biến nhất. Chu kỳ dao động ổn định của con lắc giúp đo thời gian chính xác.

Galileo Galilei đã phát hiện ra tính đẳng thời của con lắc khi quan sát một chiếc đèn chùm trong nhà thờ. Phát hiện này đã dẫn đến sự ra đời của đồng hồ quả lắc vào năm 1656 bởi Christiaan Huygens.

Ngày nay, đồng hồ quả lắc vẫn được sử dụng như một biểu tượng của sự chính xác và độ tin cậy trong đo lường thời gian.

Ứng dụng trong địa chấn kế

Con lắc đơn đóng vai trò quan trọng trong cấu tạo của địa chấn kế

• thiết bị đo động đất. Nguyên lý hoạt động dựa trên sự dao động của con lắc khi có chấn động.

Khi mặt đất rung chuyển, con lắc trong địa chấn kế sẽ dao động. Các cảm biến ghi nhận biên độ và tần số dao động, từ đó xác định được cường độ của trận động đất.

Ứng dụng trong kiến trúc và xây dựng

Các tòa nhà cao tầng thường được thiết kế với bộ giảm chấn dao động dựa trên nguyên lý con lắc. Điển hình là tòa nhà Taipei 101 ở Đài Loan sử dụng con lắc khổng lồ nặng 730 tấn.

Con lắc trong công trình xây dựng giúp hấp thụ dao động do gió mạnh hoặc động đất. Khi tòa nhà bị tác động, con lắc sẽ dao động ngược pha, giảm thiểu biên độ rung lắc của công trình.

Việc tính toán kích thước và khối lượng của con lắc phải dựa trên các thông số kỹ thuật của tòa nhà để đạt hiệu quả tối ưu.

FAQ: Câu hỏi thường gặp về con lắc đơn

Các câu hỏi thường gặp về con lắc đơn giúp học sinh hiểu sâu hơn về bản chất dao động của vật. Qua 20 năm giảng dạy, tôi nhận thấy đây là những thắc mắc phổ biến nhất.

Tại sao con lắc đơn dao động với chu kỳ không đổi?

Con lắc đơn dao động với chu kỳ không đổi nhờ nguyên lý bảo toàn năng lượng cơ học. Khi dao động, lực kéo về tỷ lệ thuận với độ lệch góc, tạo ra dao động điều hòa.

Trong quá trình dao động, năng lượng liên tục chuyển đổi qua lại giữa động năng và thế năng. Tổng năng lượng không đổi nên chu kỳ luôn ổn định.

Làm thế nào để tăng/giảm chu kỳ dao động?

Để điều chỉnh chu kỳ dao động, ta có thể thay đổi chiều dài dây hoặc gia tốc trọng trường. Công thức chu kỳ dao động là:

T = 2π√(L/g)

Trong đó:

• T là chu kỳ dao động (s)
• L là chiều dài dây (m)
• g là gia tốc trọng trường (m/s2)

Tăng chiều dài dây sẽ tăng chu kỳ dao động và ngược lại. Đây là cách đơn giản nhất để điều chỉnh chu kỳ.

Các yếu tố ảnh hưởng đến cơ năng con lắc đơn?

Cơ năng con lắc đơn phụ thuộc vào khối lượng vật nặng, chiều dài dây và biên độ dao động. Công thức cơ năng là:

E = mgh = (1/2)mgA2

Trong đó:

• E là cơ năng (J)
• m là khối lượng vật (kg)
• g là gia tốc trọng trường (m/s2)
• h là độ cao so với vị trí cân bằng (m)
• A là biên độ góc (rad)

Tăng khối lượng vật hoặc biên độ dao động sẽ làm tăng cơ năng của hệ.

Việc áp dụng công thức tính cơ năng của con lắc đơn đóng vai trò quan trọng trong nghiên cứu chuyển động dao động. Các công thức về thế năng, động năng và tổng cơ năng giúp phân tích đặc điểm dao động của vật. Kiến thức này tạo nền tảng để hiểu các ứng dụng thực tế như đồng hồ quả lắc và địa chấn kế. Học sinh cần nắm vững các công thức cơ bản để giải quyết bài tập và vận dụng trong thực tiễn.