Học công thức tính thế năng con lắc lò xo và ứng dụng thực tế
Công thức tính thế năng con lắc lò xo là kiến thức quan trọng trong chương dao động cơ học. Các yếu tố như hệ số đàn hồi và độ biến dạng quyết định giá trị thế năng đàn hồi. Quá trình chuyển hóa năng lượng tuân theo định luật bảo toàn cơ năng trong dao động điều hòa.
Công thức tính thế năng con lắc lò xo
Thế năng của con lắc lò xo là năng lượng tích trữ khi lò xo bị biến dạng. Đây là dạng năng lượng cơ học quan trọng.
Công thức tính thế năng con lắc lò xo được xác định bằng công thức:
Wt = (1/2)kx²
Trong đó:
- Wt: thế năng đàn hồi của lò xo (J)
- k: độ cứng của lò xo (N/m)
- x: độ biến dạng của lò xo (m)
Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn giữa x và Δx. Cần lưu ý x chính là độ dãn/nén của lò xo so với vị trí cân bằng.
Ví dụ: Một lò xo có độ cứng k = 100 N/m, bị kéo dãn 2cm. Thế năng của lò xo là:
- x = 0,02m
- Wt = (1/2) × 100 × (0,02)² = 0,02J
Khi giải bài tập, các em cần chú ý đổi đơn vị độ dãn sang mét (m) trước khi thế vào công thức. Sai sót này rất phổ biến khiến kết quả sai lệch 100 lần.
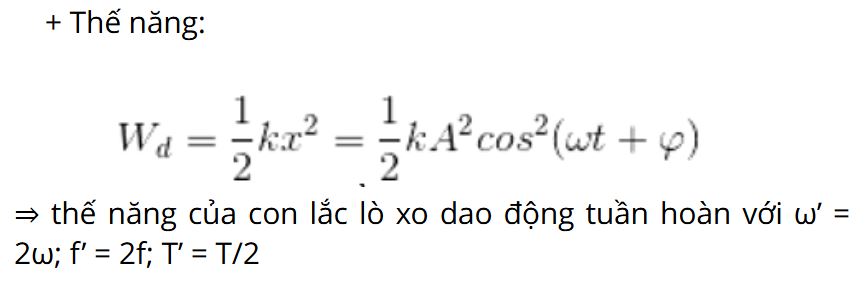
Thế năng con lắc lò xo tỉ lệ thuận với bình phương độ biến dạng. Điều này giải thích vì sao khi kéo lò xo càng dài, lực đàn hồi càng lớn và thế năng tích lũy càng nhiều.
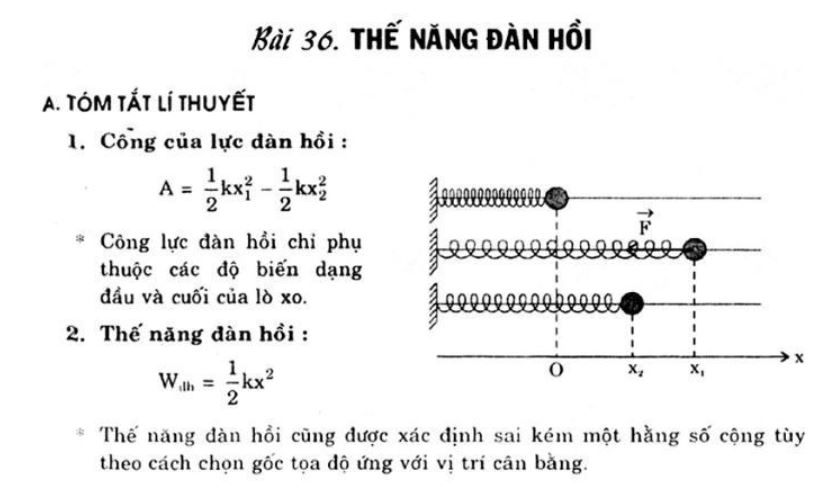
Thế năng đàn hồi và các thành phần cơ bản
Thế năng đàn hồi là dạng năng lượng tích trữ trong vật đàn hồi khi bị biến dạng. Đây là một khái niệm quan trọng trong cơ học.
Khi vật đàn hồi bị biến dạng, nó có khả năng tích trữ năng lượng và trở về trạng thái ban đầu. Công thức tính thế năng đàn hồi giúp xác định chính xác năng lượng này.
Công thức tính thế năng đàn hồi:
W = (1/2)kx²
Trong đó:
- W là thế năng đàn hồi (J)
- k là hệ số đàn hồi (N/m)
- x là độ biến dạng (m)
Thế năng lò xo là gì và ý nghĩa vật lý
Thế năng lò xo là năng lượng được tích trữ trong lò xo khi nó bị nén hoặc giãn ra khỏi vị trí cân bằng.
Khi lò xo bị biến dạng, các phân tử trong lò xo bị dịch chuyển khỏi vị trí ban đầu. Điều này tạo ra lực đàn hồi có xu hướng đưa lò xo về trạng thái cân bằng.
Trong thực tế giảng dạy, tôi thường ví von thế năng lò xo giống như “năng lượng ngủ”
- nó chỉ “thức dậy” khi lò xo bị tác động và biến dạng.
Hệ số đàn hồi k và vai trò trong dao động
Hệ số đàn hồi lò xo k đặc trưng cho độ cứng của lò xo. Giá trị k càng lớn thì lò xo càng khó biến dạng.
Trong dao động điều hòa, k quyết định chu kỳ và tần số dao động tự nhiên của hệ:
T = 2π√(m/k)
Với m là khối lượng vật gắn vào lò xo.
Kinh nghiệm 20 năm giảng dạy cho thấy học sinh thường nhớ tốt hơn khi tôi so sánh k với “sức đề kháng” của lò xo
- giống như người càng khỏe thì càng khó bị đẩy.
Độ biến dạng của lò xo và cách xác định
Độ biến dạng lò xo là khoảng cách từ vị trí cân bằng đến vị trí lò xo bị kéo/nén. Nó được tính bằng công thức:
Δl = F/k
Trong đó:
- Δl là độ biến dạng (m)
- F là lực tác dụng (N)
- k là hệ số đàn hồi (N/m)
Để xác định chính xác độ biến dạng, cần đánh dấu vị trí cân bằng của lò xo trước khi tác dụng lực. Sau đó đo khoảng cách từ điểm đánh dấu đến vị trí mới của lò xo.
Phân tích công thức thế năng con lắc lò xo trong dao động điều hòa
Thế năng của con lắc lò xo là dạng năng lượng thế đàn hồi. Nó phụ thuộc vào độ biến dạng của lò xo khi dao động.

Khi con lắc dao động, thế năng chuyển hóa qua lại với động năng. Đây là quá trình bảo toàn cơ năng trong dao động điều hòa.
Biểu thức toán học và các đại lượng liên quan
Công thức tính thế năng con lắc lò xo được biểu diễn:
Wt = (1/2)kx2
Trong đó:
- k là độ cứng của lò xo (N/m)
- x là độ biến dạng của lò xo (m)
Độ biến dạng x liên hệ với công thức lorenxo thông qua lực đàn hồi của lò xo.
Mối quan hệ giữa thế năng và biên độ dao động
Thế năng đạt giá trị cực đại khi biên độ dao động con lắc lò xo đạt giá trị lớn nhất.
Tại vị trí cân bằng, thế năng bằng 0 vì độ biến dạng x = 0.
Đồ thị thế năng theo thời gian có dạng parabol, đối xứng qua trục thẳng đứng.
Thế năng đàn hồi cực đại và điều kiện xảy ra
Thế năng đàn hồi cực đại xuất hiện tại hai vị trí biên. Giá trị này được tính:
Wtmax = (1/2)kA2
Với A là biên độ dao động.
Điều kiện để đạt thế năng cực đại:
- Vận tốc của vật bằng 0
- Độ biến dạng của lò xo đạt giá trị cực đại
- Toàn bộ cơ năng chuyển hóa thành thế năng
Mối quan hệ giữa thế năng và cơ năng trong dao động
Trong dao động điều hòa của con lắc lò xo, năng lượng được chuyển hóa liên tục giữa thế năng và động năng. Công thức tính năng lượng của con lắc lò xo phụ thuộc vào vị trí và vận tốc của vật.
Khi vật dao động, tổng của thế năng và động năng luôn không đổi và bằng cơ năng. Công thức tính cơ năng của lò xo được xác định bởi biên độ dao động:
W = 1/2 × k × A²
Trong đó:
- W là cơ năng (J)
- k là độ cứng của lò xo (N/m)
- A là biên độ dao động (m)
Chuyển hóa năng lượng trong dao động điều hòa
Quá trình chuyển hóa năng lượng diễn ra liên tục trong dao động điều hòa. Tại vị trí cân bằng, toàn bộ năng lượng tồn tại dưới dạng động năng.
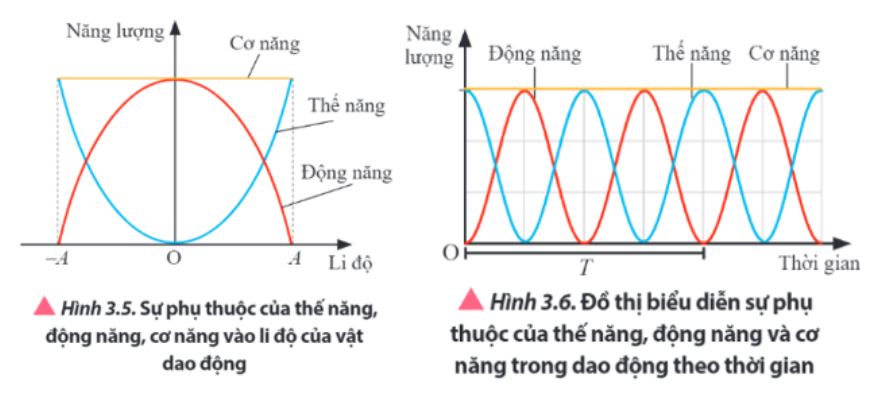
Khi vật chuyển động ra xa vị trí cân bằng, động năng giảm dần và chuyển hóa thành thế năng. Tại biên độ, toàn bộ năng lượng chuyển thành thế năng.
Quá trình này lặp đi lặp lại theo chu kỳ dao động, tạo nên sự chuyển hóa qua lại giữa hai dạng năng lượng. Bạn có thể tham khảo thêm về công thức tính cơ năng của con lắc đơn để hiểu rõ hơn.
Bảo toàn cơ năng của con lắc lò xo
Trong điều kiện lý tưởng không có ma sát, cơ năng của con lắc lò xo được bảo toàn. Điều này có nghĩa tổng của thế năng và động năng luôn không đổi tại mọi thời điểm.
Nguyên lý bảo toàn cơ năng được thể hiện qua công thức:
W = Wđ + Wt = 1/2 × m × v² + 1/2 × k × x²
Với:
- Wđ là động năng
- Wt là thế năng
- m là khối lượng vật (kg)
- v là vận tốc tức thời (m/s)
- x là li độ (m)
Thế năng con lắc lò xo tại các vị trí đặc biệt
Thế năng con lắc lò xo dao động đạt giá trị cực đại tại biên độ và cực tiểu tại vị trí cân bằng. Tại biên độ, thế năng bằng cơ năng:
Wt(max) = 1/2 × k × A²
Tại vị trí cân bằng, thế năng bằng 0. Bạn có thể tìm hiểu thêm về công thức thế năng con lắc đơn để so sánh sự khác biệt.
Trong thực tế giảng dạy, tôi thường yêu cầu học sinh vẽ đồ thị biểu diễn sự biến thiên của thế năng theo thời gian. Điều này giúp các em hình dung rõ hơn về quy luật dao động.
FAQ: Câu hỏi thường gặp về thế năng con lắc lò xo
Khi học về công thức tính thế năng con lắc lò xo, học sinh thường gặp nhiều thắc mắc. Tôi sẽ giải đáp một số câu hỏi phổ biến nhất sau 20 năm giảng dạy môn Vật lý.
Làm thế nào để xác định hệ số đàn hồi k của lò xo?
Hệ số đàn hồi k có thể xác định bằng phương pháp thực nghiệm đơn giản. Treo một vật nặng có khối lượng m vào lò xo và đo độ giãn Δx của lò xo.
Áp dụng định luật Hooke, ta có công thức:
k = F/Δx = mg/Δx
Trong đó:
- k là hệ số đàn hồi (N/m)
- m là khối lượng vật (kg)
- g là gia tốc trọng trường (9.8 m/s2)
- Δx là độ giãn của lò xo (m)
Tại sao thế năng con lắc lò xo lại biến thiên tuần hoàn?
Thế năng con lắc lò xo biến thiên tuần hoàn do chuyển động dao động của vật. Khi vật dao động, vị trí của nó thay đổi liên tục theo chu kỳ.
Tại vị trí cân bằng, thế năng đạt giá trị nhỏ nhất. Tại biên độ dao động, thế năng đạt giá trị lớn nhất. Sự chuyển đổi qua lại này tạo nên tính tuần hoàn.
Thế năng con lắc lò xo phụ thuộc vào những yếu tố nào?
Thế năng con lắc lò xo phụ thuộc vào hai yếu tố chính. Đó là hệ số đàn hồi k của lò xo và độ biến dạng x của lò xo.
Công thức tính thế năng:
Wt = (1/2)kx2
Trong đó:
- Wt là thế năng đàn hồi (J)
- k là hệ số đàn hồi của lò xo (N/m)
- x là độ biến dạng của lò xo (m)
Khi độ biến dạng x tăng, thế năng tăng theo hàm bậc hai. Điều này giải thích tại sao thế năng tăng nhanh khi lò xo bị nén hoặc giãn nhiều.
Việc áp dụng công thức tính thế năng con lắc lò xo đóng vai trò quan trọng trong nghiên cứu dao động điều hòa. Các yếu tố như hệ số đàn hồi k, độ biến dạng và biên độ dao động tạo nên bức tranh tổng thể về năng lượng của hệ dao động. Sự chuyển hóa giữa thế năng và động năng tuân theo định luật bảo toàn cơ năng, giúp dự đoán chính xác trạng thái dao động của vật. Kiến thức này tạo nền tảng vững chắc cho việc giải các bài toán về dao động cơ học.
Bài viết liên quan

Phân tích công thức dao động tắt dần và ứng dụng trong vật lý
Tìm hiểu chi tiết công thức dao động tắt dần qua các khái niệm, đặc điểm và ứng dụng thực tế. Phân tích phương trình, biên độ, chu kỳ cùng các bài tập minh họa dễ hiểu.

Công thức dao động điện từ và các ứng dụng trong mạch LC cơ bản
Tìm hiểu công thức dao động điện từ trong mạch LC với các yếu tố cơ bản, năng lượng, chu kỳ và ứng dụng thực tế. Giải thích chi tiết cho học sinh dễ hiểu.

Tìm hiểu công thức tính li độ cực đại và ứng dụng trong dao động điều hòa
Tìm hiểu công thức tính li độ cực đại trong dao động điều hòa, mối quan hệ với biên độ và các đại lượng vật lý. Hướng dẫn chi tiết cách xác định qua đồ thị và bài tập.

Thuộc lòng công thức tính chiều dài quỹ đạo và các đường cong cơ bản
Tìm hiểu công thức tính chiều dài quỹ đạo cho chuyển động tròn, elip và các đường cong. Hướng dẫn chi tiết cách áp dụng công thức với bài tập từ cơ bản đến nâng cao.

Nắm rõ công thức dao động cơ và các dạng dao động điều hòa cơ bản
Tìm hiểu công thức dao động cơ qua các khái niệm cơ bản về dao động điều hòa, tắt dần và cưỡng bức. Phân tích chi tiết biên độ, tần số, chu kỳ và pha dao động trong vật lý phổ thông.

Tổng quan công thức tính vận tốc góc và ứng dụng trong vật lý
Tìm hiểu công thức tính vận tốc góc và cách áp dụng trong chuyển động tròn đều. Giải thích chi tiết khái niệm, đơn vị đo và mối quan hệ với vận tốc dài kèm bài tập minh họa.

