Tìm hiểu công thức tính gia tốc trung bình và ứng dụng thực tế

Công thức tính gia tốc trung bình là nền tảng quan trọng trong vật lý. Các yếu tố như vận tốc, thời gian và lực tác động đều ảnh hưởng đến gia tốc. Bài viết phân tích chi tiết cách áp dụng công thức cho từng dạng chuyển động cụ thể.

Công thức tính gia tốc trung bình

Gia tốc trung bình là đại lượng mô tả sự thay đổi vận tốc của vật trong một khoảng thời gian. Đây là khái niệm quan trọng trong động học.

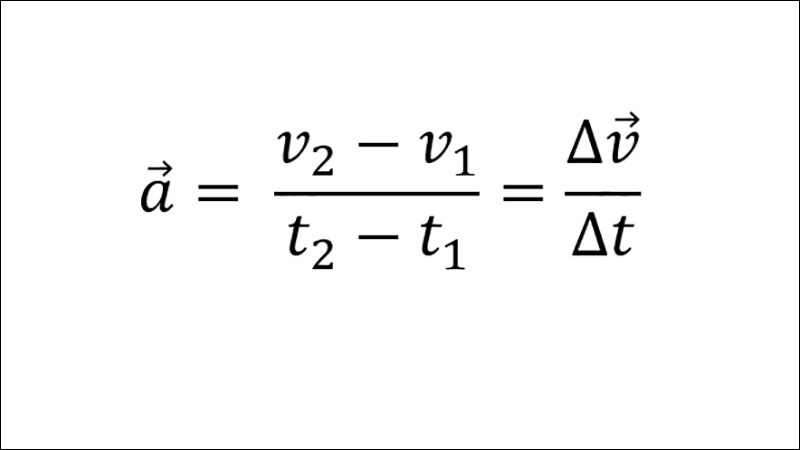
Công thức tính gia tốc trung bình được biểu diễn như sau:

atb = Δv/Δt = (v2

• v1)/(t2 - t1)

Trong đó:

• atb: gia tốc trung bình (m/s2)
• v2: vận tốc tại thời điểm sau (m/s)
• v1: vận tốc tại thời điểm đầu (m/s)
• t2: thời điểm sau (s)
• t1: thời điểm đầu (s)

Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn giữa v2 và v1. Cách ghi nhớ đơn giản là v2 luôn là vận tốc ở thời điểm sau.

Ví dụ: Một ô tô tăng tốc từ 0 m/s đến 20 m/s trong 5 giây. Gia tốc trung bình sẽ là:

atb = (20

• 0)/(5 - 0) = 4 m/s2

Lưu ý khi sử dụng công thức:

• Đơn vị của vận tốc phải thống nhất
• Thời gian phải được tính bằng giây
• Kết quả có thể dương hoặc âm tùy chiều chuyển động

Với công thức này, bạn có thể dễ dàng tính toán sự thay đổi vận tốc của vật theo thời gian.

Các yếu tố ảnh hưởng đến gia tốc trung bình trong chuyển động

Công thức tính gia tốc trung bình là một trong những công thức quan trọng trong vật lý. Gia tốc trung bình phụ thuộc vào nhiều yếu tố khác nhau và có mối liên hệ mật thiết với chuyển động của vật.

Để hiểu rõ hơn về các yếu tố ảnh hưởng, chúng ta sẽ phân tích từng thành phần cụ thể. Mỗi yếu tố đều có vai trò riêng và tác động trực tiếp đến giá trị gia tốc.

Sự thay đổi vận tốc theo thời gian

Vận tốc thay đổi là yếu tố quyết định chính đến gia tốc trung bình của vật. Khi vận tốc thay đổi nhanh, gia tốc sẽ lớn và ngược lại.

Trong thực tế giảng dạy, tôi thường lấy ví dụ về việc tăng tốc của ô tô. Khi ô tô tăng từ 0-100km/h trong 10 giây sẽ có gia tốc lớn hơn khi tăng cùng vận tốc đó trong 20 giây.

Ảnh hưởng của lực tác động

Lực tác động càng lớn thì gia tốc càng tăng. Điều này được thể hiện qua định luật II Newton:

a = F/m

Trong đó:

• a: gia tốc (m/s2)
• F: lực tác dụng (N)
• m: khối lượng vật (kg)

Khi giảng dạy về công thức tính gia tốc trọng trường, tôi thường nhấn mạnh mối quan hệ tỷ lệ thuận giữa lực và gia tốc.

Vai trò của khối lượng vật

Khối lượng vật có tác động ngược chiều với gia tốc. Vật có khối lượng càng lớn thì gia tốc càng nhỏ khi chịu cùng một lực tác dụng.

Tôi thường minh họa bằng việc đẩy một chiếc xe đạp và một chiếc ô tô. Với cùng lực đẩy, xe đạp sẽ đạt gia tốc lớn hơn nhiều so với ô tô do khối lượng nhỏ hơn.

Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường dễ nhớ và hiểu bài hơn khi được liên hệ với các ví dụ thực tế gần gũi như vậy.

Phương pháp tính gia tốc trung bình trong các dạng chuyển động

Gia tốc trung bình là đại lượng mô tả sự thay đổi vận tốc của vật trong một khoảng thời gian. Công thức tính gia tốc trung bình cơ bản là tỉ số giữa độ biến thiên vận tốc và khoảng thời gian:

atb = Δv/Δt = (v2

• v1)/(t2 - t1)

Trong đó:

• atb: gia tốc trung bình (m/s2)
• v2, v1: vận tốc tại thời điểm sau và trước (m/s)
• t2, t1: thời điểm sau và trước (s)

Chuyển động thẳng đều và biến đổi đều

Với chuyển động thẳng đều, gia tốc trung bình bằng 0 do vận tốc không đổi. Còn với chuyển động thẳng biến đổi đều, gia tốc trung bình chính là gia tốc tức thời:

a = (v

• v0)/t

Trong đó:

• a: gia tốc (m/s2)
• v: vận tốc tại thời điểm t (m/s)
• v0: vận tốc ban đầu (m/s)
• t: thời gian chuyển động (s)

Chuyển động tròn và chuyển động cong

Với chuyển động tròn đều, gia tốc hướng tâm được tính theo công thức tính vận tốc góc:

aht = v2/R = ω2R

Trong đó:

• aht: gia tốc hướng tâm (m/s2)
• v: vận tốc dài (m/s)
• R: bán kính quỹ đạo (m)
• ω: vận tốc góc (rad/s)

Với chuyển động cong, gia tốc toàn phần là tổng hợp của gia tốc tiếp tuyến và gia tốc hướng tâm.

Chuyển động rơi tự do

Trong chuyển động rơi tự do, gia tốc không đổi và bằng gia tốc trọng trường g ≈ 9,8 m/s2. Vận tốc của vật khi chạm đất có thể tính theo công thức tính vận tốc khi chạm đất:

v = v0 + gt

Trong đó:

• v: vận tốc khi chạm đất (m/s)
• v0: vận tốc ban đầu (m/s)
• g: gia tốc trọng trường (m/s2)
• t: thời gian rơi (s)

Ứng dụng công thức gia tốc trung bình trong thực tế

Công thức tính gia tốc trung bình được áp dụng rộng rãi để phân tích chuyển động của vật thể. Công thức giúp xác định mức độ thay đổi vận tốc theo thời gian một cách chính xác và khoa học.

Việc nắm vững công thức và cách áp dụng sẽ giúp giải quyết nhiều bài toán trong học tập và thực tiễn. Các lĩnh vực ứng dụng chính bao gồm tính toán vật lý, kỹ thuật công nghiệp và đời sống hàng ngày.

Tính toán trong các bài toán vật lý

Trong giải các bài tập vật lý, công thức gia tốc trung bình thường xuất hiện kết hợp với công thức tính tốc độ dài. Điều quan trọng là xác định đúng các đại lượng cần tìm.

Khi giải bài tập về chuyển động thẳng biến đổi đều, ta cần chú ý đến dấu của gia tốc. Gia tốc dương thể hiện chuyển động nhanh dần đều và gia tốc âm thể hiện chuyển động chậm dần đều.

Một kinh nghiệm tôi thường chia sẻ với học sinh là vẽ đồ thị vận tốc-thời gian để hình dung rõ hơn về gia tốc trung bình. Độ dốc của đường thẳng chính là gia tốc trung bình của chuyển động.

Ứng dụng trong kỹ thuật và công nghiệp

Ngành công nghiệp ô tô sử dụng gia tốc trung bình để thiết kế hệ thống phanh và tăng tốc. Các kỹ sư phải tính toán kỹ lưỡng để đảm bảo an toàn cho người sử dụng.

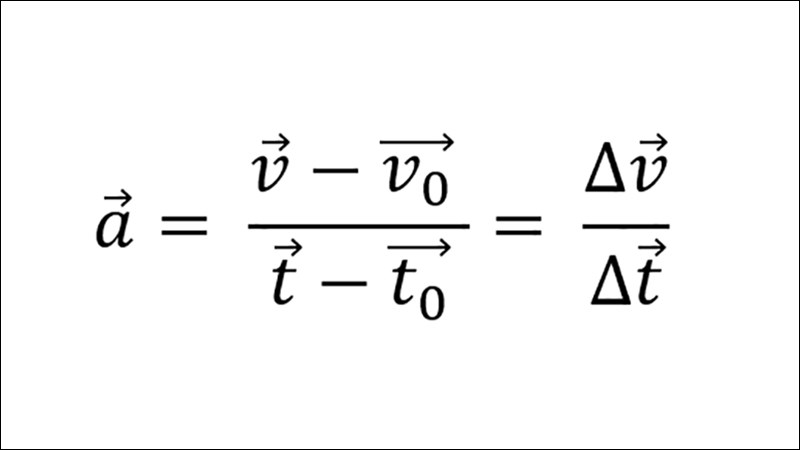
Trong ngành hàng không, công thức tính vận tốc dòng chảy và gia tốc trung bình giúp tính toán lực tác động lên máy bay. Từ đó thiết kế được cánh máy bay tối ưu.

Các robot công nghiệp cũng được lập trình dựa trên tính toán gia tốc trung bình. Điều này giúp robot di chuyển chính xác và mượt mà trong quá trình sản xuất.

Ứng dụng trong đời sống hàng ngày

Gia tốc trung bình xuất hiện trong nhiều hoạt động thường ngày như lái xe, chơi thể thao. Khi đạp xe đạp lên dốc, ta cần điều chỉnh lực đạp để có gia tốc phù hợp.

Các vận động viên điền kinh sử dụng gia tốc trung bình để phân tích và cải thiện kỹ thuật chạy. Họ tập trung vào giai đoạn tăng tốc để đạt thành tích tốt nhất.

Ngay cả việc đi thang máy cũng liên quan đến gia tốc trung bình. Thang máy được thiết kế để có gia tốc phù hợp, tránh gây khó chịu cho người sử dụng.

FAQ: Câu hỏi thường gặp về gia tốc trung bình

Gia tốc trung bình là một khái niệm quan trọng trong vật lý. Tôi sẽ giải đáp các câu hỏi thường gặp về chủ đề này.

• Gia tốc trung bình có thể âm không?

Gia tốc trung bình có thể mang giá trị âm. Điều này xảy ra khi vật chuyển động chậm dần. Để tính toán chính xác, bạn cần nắm vững công thức tính độ giảm thế.

• Làm sao phân biệt gia tốc trung bình và tức thời?

Gia tốc trung bình tính trong một khoảng thời gian. Gia tốc tức thời tính tại một thời điểm. Hiểu rõ công thức tính tốc độ truyền sóng giúp phân biệt tốt hơn.

• Gia tốc trung bình trong dao động điều hòa?

Trong dao động điều hòa, gia tốc trung bình phụ thuộc vào công thức chu kì dao động điều hòa và biên độ dao động.

• Gia tốc trung bình có liên quan đến pha dao động?

Gia tốc trung bình có mối liên hệ với công thức tính pha ban đầu trong chuyển động dao động điều hòa.

• Gia tốc trung bình có bằng 0 không?

Gia tốc trung bình có thể bằng 0 khi vận tốc không đổi hoặc vật chuyển động đều.

Việc áp dụng công thức tính gia tốc trung bình đóng vai trò quan trọng trong nghiên cứu chuyển động của vật. Các yếu tố như sự thay đổi vận tốc, lực tác động và khối lượng vật ảnh hưởng trực tiếp đến giá trị gia tốc trung bình. Công thức này giúp giải quyết nhiều bài toán vật lý và ứng dụng thực tiễn trong kỹ thuật, công nghiệp và đời sống hàng ngày.