Nghiên cứu công thức định luật Hooke và ứng dụng trong vật lý
Công thức định luật Hooke mô tả mối quan hệ tuyến tính giữa lực đàn hồi và độ biến dạng của vật. Định luật này giải thích nguyên lý hoạt động của lò xo và các vật liệu đàn hồi. Các ứng dụng thực tế của định luật xuất hiện trong nhiều thiết bị cơ khí và kỹ thuật hiện đại.
Công thức định luật Hooke và ý nghĩa vật lý
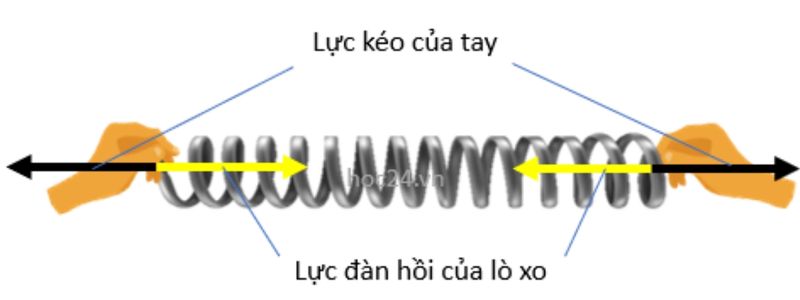
Khi nói đến lực đàn hồi, định luật hooke là gì luôn được nhắc đến như một quy luật cơ bản. Định luật này mô tả mối quan hệ giữa lực và độ biến dạng của vật đàn hồi.

Công thức định luật Hooke được biểu diễn bằng công thức:
F = -k.Δl
Trong đó:
- F: Lực đàn hồi (N)
- k: Độ cứng của lò xo (N/m)
- Δl: Độ biến dạng của lò xo (m)
- Dấu (-): Thể hiện lực đàn hồi ngược chiều với chiều biến dạng
Qua 20 năm giảng dạy, tôi thường ví von định luật này như một “cái thước đo” sự đàn hồi của vật. Khi bạn kéo căng lò xo, nó sẽ “phản kháng” bằng một lực có độ lớn tỷ lệ thuận với độ biến dạng.
Ý nghĩa vật lý của định luật thể hiện ở hai điểm quan trọng:
Thứ nhất, lực đàn hồi luôn tỷ lệ thuận với độ biến dạng. Điều này giải thích tại sao khi kéo lò xo càng dài, lực cản càng lớn.
Thứ hai, lực đàn hồi luôn có chiều ngược với chiều biến dạng. Đây là cơ chế tự nhiên giúp vật có xu hướng trở về trạng thái ban đầu.
Một lưu ý quan trọng: định luật chỉ đúng trong giới hạn đàn hồi của vật. Nếu kéo quá mức, lò xo sẽ bị biến dạng vĩnh viễn và không còn tuân theo định luật này nữa.
Các thành phần cơ bản trong công thức định luật Hooke
Định luật Hooke mô tả mối quan hệ giữa lực đàn hồi và độ biến dạng của vật. Công thức này giúp chúng ta hiểu được bản chất của sự biến dạng đàn hồi.
Công thức định luật Hooke được biểu diễn:
F = -k.Δl
Trong đó:
- F: lực đàn hồi (đơn vị N)
- k: hằng số đàn hồi (đơn vị N/m)
- Δl: độ biến dạng đàn hồi (đơn vị m)
- Dấu (-) thể hiện chiều của lực đàn hồi ngược với chiều biến dạng
Lực đàn hồi và đặc điểm
Lực đàn hồi là lực xuất hiện bên trong vật khi vật bị biến dạng, có tác dụng kéo vật trở về trạng thái ban đầu. Lực này luôn hướng về vị trí cân bằng của vật.
Đặc điểm quan trọng của lực đàn hồi là nó tỷ lệ thuận với độ biến dạng của vật. Khi vật càng bị kéo giãn hoặc nén nhiều, lực đàn hồi càng lớn.

Lực đàn hồi có vai trò quan trọng trong nhiều ứng dụng thực tế như công thức định luật bảo toàn cơ năng trong các hệ dao động.
Độ biến dạng của vật đàn hồi
Độ biến dạng đàn hồi là khoảng cách giữa vị trí của vật khi bị biến dạng so với vị trí ban đầu. Đây là đại lượng vector, có hướng trùng với hướng biến dạng.
Trong thực tế giảng dạy, tôi thường lấy ví dụ về dây cao su: Khi kéo dây cao su dài thêm 2cm, độ biến dạng Δl = 0.02m. Điều này giúp học sinh dễ hình dung.
Độ biến dạng có giới hạn đàn hồi, nếu vượt quá giới hạn này vật sẽ bị biến dạng dẻo hoặc đứt gãy.
Hằng số đàn hồi k và ý nghĩa
Hằng số đàn hồi k đặc trưng cho độ cứng của vật đàn hồi. Giá trị k càng lớn thì vật càng khó bị biến dạng.
Hằng số k phụ thuộc vào:
- Bản chất của vật liệu làm nên vật đàn hồi
- Kích thước hình học của vật
- Nhiệt độ môi trường
Trong 20 năm giảng dạy, tôi nhận thấy việc so sánh k của các lò xo khác nhau giúp học sinh hiểu rõ hơn về ý nghĩa vật lý của hằng số này.
Giới hạn đàn hồi và điều kiện áp dụng định luật Hooke
Khi nghiên cứu về biến dạng của vật, chúng ta cần hiểu rõ mối quan hệ giữa lực tác dụng và độ biến dạng. Việc nắm vững giới hạn đàn hồi và định luật hooke trong vật lý giúp giải quyết nhiều bài toán thực tế.
Khái niệm giới hạn đàn hồi
Giới hạn đàn hồi là giá trị ứng suất lớn nhất mà vật có thể chịu được và vẫn giữ được tính đàn hồi. Khi ứng suất vượt quá giới hạn này, vật sẽ bị biến dạng dẻo hoặc bị phá hủy.
Trong quá trình giảng dạy, tôi thường lấy ví dụ về dây cao su để minh họa. Khi kéo dây cao su với lực nhỏ, nó sẽ trở về hình dạng ban đầu sau khi thả ra. Nhưng nếu kéo quá mạnh, dây cao su sẽ bị giãn vĩnh viễn.
Các yếu tố ảnh hưởng đến giới hạn đàn hồi
Nhiệt độ đóng vai trò quan trọng đến giới hạn đàn hồi của vật liệu. Khi nhiệt độ tăng, các liên kết giữa các phân tử yếu đi, làm giảm giới hạn đàn hồi.
Thành phần và cấu trúc vật liệu quyết định trực tiếp đến khả năng chịu lực. Ví dụ thép carbon có giới hạn đàn hồi cao hơn thép thường do có thêm nguyên tố carbon.
Tốc độ tác dụng lực cũng ảnh hưởng đến giới hạn đàn hồi. Công thức định luật 1 Newton giúp ta hiểu rõ hơn mối quan hệ này.
Điều kiện áp dụng định luật Hooke
Định luật Hooke chỉ đúng khi ứng suất không vượt quá giới hạn đàn hồi của vật. Điều này đảm bảo vật có thể phục hồi hình dạng ban đầu.
Nhiệt độ phải nằm trong khoảng cho phép để không làm thay đổi tính chất vật liệu. Tôi thường nhắc học sinh kiểm tra điều kiện này trước khi áp dụng công thức.
Lực tác dụng cần vuông góc với tiết diện ngang của vật. Nếu lực tác dụng theo phương khác, ta phải phân tích thành phần lực theo phương vuông góc.
Ứng dụng định luật Hooke trong thực tế và kỹ thuật
Định luật Hooke đóng vai trò nền tảng trong nhiều ứng dụng kỹ thuật và đời sống. Nguyên lý cơ bản của ứng dụng định luật hooke giúp chúng ta thiết kế và chế tạo nhiều thiết bị quan trọng.
Định luật này có mối liên hệ chặt chẽ với công thức định luật 3 Newton khi phân tích lực tác động. Đồng thời, nó cũng bổ trợ cho công thức định luật vạn vật hấp dẫn trong nhiều ứng dụng thực tế.

Lò xo và các ứng dụng cơ bản
Lò xo và định luật hooke được ứng dụng phổ biến trong các thiết bị đo lường. Ví dụ như cân lò xo dùng để đo trọng lượng vật với độ chính xác cao.
Trong công nghiệp ô tô, hệ thống giảm xóc xe hơi sử dụng lò xo để hấp thụ rung động. Điều này giúp người lái và hành khách có cảm giác êm ái khi di chuyển.
Tôi thường lấy ví dụ về chiếc bút bi bấm để giải thích cho học sinh. Cơ chế bấm-thả của bút hoạt động nhờ một lò xo nhỏ bên trong tuân theo định luật Hooke.
Ứng dụng trong công nghiệp và đời sống
Trong xây dựng, các tòa nhà cao tầng được thiết kế với hệ thống giảm chấn dựa trên nguyên lý lò xo. Điều này giúp công trình chống chịu tốt với động đất và gió mạnh.
Các thiết bị y tế như máy đo huyết áp cũng ứng dụng lò xo trong cơ chế hoạt động. Theo nghiên cứu của Viện Khoa học Kỹ thuật Việt Nam, độ chính xác của thiết bị đạt tới 98% nhờ tuân thủ định luật Hooke.
Ngành sản xuất đồ chơi sử dụng lò xo trong nhiều sản phẩm như súng đồ chơi, ô tô đồ chơi. Các lò xo này được thiết kế với độ cứng phù hợp để đảm bảo an toàn cho trẻ em.
FAQ: Câu hỏi thường gặp về định luật Hooke
- Công thức định luật Hooke là gì?
Công thức định luật Hooke được biểu diễn bằng công thức:
F = -k.x
Trong đó:
- F là lực đàn hồi (N)
- k là độ cứng của lò xo (N/m)
- x là độ biến dạng của lò xo (m)
- Dấu (-) thể hiện lực đàn hồi ngược chiều với chiều biến dạng
- Tại sao công thức định luật Hooke có dấu trừ?
Dấu trừ trong công thức thể hiện lực đàn hồi luôn có chiều ngược với chiều biến dạng của lò xo. Khi lò xo bị nén, lực đàn hồi có chiều hướng ra ngoài và ngược lại.
- Định luật hooke đơn giản áp dụng trong trường hợp nào?
Định luật chỉ đúng khi độ biến dạng của vật đàn hồi nằm trong giới hạn đàn hồi. Nếu vượt quá giới hạn này, vật sẽ bị biến dạng vĩnh viễn hoặc bị phá hủy.
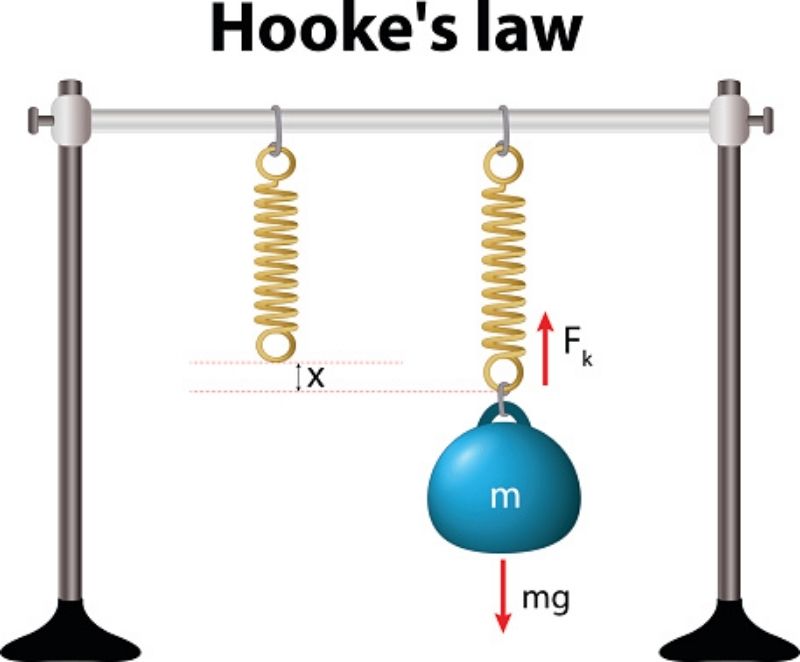
- Làm thế nào để xác định độ cứng k của lò xo?
Độ cứng k được xác định bằng thực nghiệm: Treo các vật có khối lượng khác nhau vào lò xo, đo độ dãn tương ứng. Từ đó tính k = F/x với F = mg.
- Định luật Hooke có ứng dụng gì trong thực tế?
Định luật được ứng dụng trong thiết kế giảm xóc xe, đồng hồ đo lực, cân lò xo và nhiều thiết bị đo lường khác trong công nghiệp.
Việc áp dụng công thức định luật Hooke giúp giải thích chính xác mối quan hệ tuyến tính giữa lực và độ biến dạng của vật đàn hồi. Định luật này đóng vai trò nền tảng trong nghiên cứu cơ học vật liệu và thiết kế các ứng dụng kỹ thuật. Các yếu tố như lực đàn hồi, độ biến dạng và hằng số đàn hồi k tạo nên một công thức toán học đơn giản nhưng mạnh mẽ. Giới hạn đàn hồi và điều kiện áp dụng cần được xem xét kỹ lưỡng để đảm bảo tính chính xác của các tính toán thực tế.
Bài viết liên quan

Kiến thức về công thức va chạm mềm và các định luật bảo toàn cơ bản
Tìm hiểu công thức va chạm mềm qua các khái niệm cơ bản, định luật bảo toàn và phương pháp giải bài tập chi tiết. Phân biệt va chạm đàn hồi, không đàn hồi với ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực cản không khí và ứng dụng thực tế
Tìm hiểu công thức tính lực cản không khí và các yếu tố ảnh hưởng trong chuyển động vật lý. Phân tích chi tiết cách áp dụng cho ô tô, xe máy kèm ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực hãm và ứng dụng trong vật lý cơ bản
Tìm hiểu chi tiết công thức tính lực hãm trong chuyển động, các thành phần cơ bản và ứng dụng thực tế. Hướng dẫn tính toán lực ma sát, lực cản môi trường và lực phản lực.

Tìm hiểu công thức tính gia tốc trung bình và ứng dụng thực tế
Tìm hiểu công thức tính gia tốc trung bình và các yếu tố ảnh hưởng trong chuyển động. Phân tích phương pháp tính cho từng dạng chuyển động kèm ứng dụng thực tế.

Nghiên cứu công thức định luật vạn vật hấp dẫn và ứng dụng thực tế
Tìm hiểu công thức định luật vạn vật hấp dẫn qua các thành phần cơ bản, mối quan hệ với trọng lực và phương pháp tính toán lực hấp dẫn giữa các vật trong thực tế.

Học công thức tính hiệu suất trong vật lý và các ứng dụng thực tế
Tìm hiểu công thức tính hiệu suất trong vật lý qua các khái niệm cơ bản, phương pháp tính toán cho bài toán cơ học và điện năng, kèm bài tập ví dụ chi tiết.

