Khái quát công thức lực li tâm và ứng dụng trong thực tiễn
Công thức lực li tâm giúp giải thích nhiều hiện tượng vật lý thú vị trong cuộc sống. Các yếu tố như khối lượng, vận tốc góc và bán kính quỹ đạo quyết định độ lớn của lực này. Việc nắm vững công thức và phương pháp giải mở ra nhiều ứng dụng quan trọng trong công nghiệp và kỹ thuật hiện đại.
Công thức lực li tâm là gì?
Lực li tâm là lực hướng ra xa tâm quỹ đạo của vật chuyển động tròn. Công thức lực li tâm được biểu diễn như sau:
F = mv²/R
Trong đó:
- F: Lực li tâm (N)
- m: Khối lượng vật (kg)
- v: Vận tốc dài của vật (m/s)
- R: Bán kính quỹ đạo tròn (m)
Qua 20 năm giảng dạy, tôi thường ví von lực li tâm giống như cảm giác bị đẩy ra ngoài khi ngồi ô tô vào cua gấp. Càng vào cua nhanh, lực đẩy càng mạnh.
Để giúp học sinh dễ nhớ, tôi thường nhấn mạnh mối quan hệ giữa các đại lượng:
- Lực li tâm tỷ lệ thuận với khối lượng vật
- Lực li tâm tỷ lệ thuận với bình phương vận tốc
- Lực li tâm tỷ lệ nghịch với bán kính quỹ đạo
Ví dụ thực tế: Khi tàu lượn siêu tốc chạy trong đường vòng, lực li tâm có thể lên tới 3-4G (3-4 lần trọng lượng cơ thể). Đó là lý do bạn cảm thấy như bị đẩy mạnh ra phía ngoài.
Một lưu ý quan trọng khi sử dụng công thức: Đơn vị của các đại lượng phải thống nhất theo hệ SI để kết quả chính xác.
Các yếu tố ảnh hưởng đến lực li tâm trong chuyển động tròn
Lực li tâm là lực hướng tâm xuất hiện trong chuyển động tròn đều. Công thức lực li tâm được xác định bởi công thức
F = mω²R.
Để hiểu rõ hơn về lực li tâm, chúng ta cần phân tích 3 yếu tố chính ảnh hưởng đến độ lớn của nó. Mỗi yếu tố đóng vai trò quan trọng và tác động trực tiếp đến giá trị của lực li tâm.
Khối lượng vật chuyển động
Khối lượng vật chuyển động tỷ lệ thuận với lực li tâm. Khi khối lượng vật tăng lên gấp đôi, lực li tâm cũng tăng gấp đôi.
Trong thực tế giảng dạy, tôi thường lấy ví dụ về việc quay dây có buộc vật nặng. Học sinh dễ dàng nhận thấy khi buộc vật nặng hơn, tay phải giữ chặt hơn để chống lại lực kéo mạnh hơn.
Vận tốc góc của vật
Vận tốc góc ảnh hưởng mạnh nhất đến lực li tâm vì nó được bình phương trong công thức. Điều này giải thích Công thức tính li độ cực đại khi vật chuyển động tròn.
Tôi thường minh họa bằng thí nghiệm quay nước trong xô. Khi tăng tốc độ quay, nước dâng cao hơn ở thành xô do lực li tâm tăng mạnh theo bình phương vận tốc góc.
Bán kính quỹ đạo chuyển động
Bán kính quỹ đạo tỷ lệ thuận với lực li tâm. Khi bán kính tăng, lực li tâm tăng tương ứng.
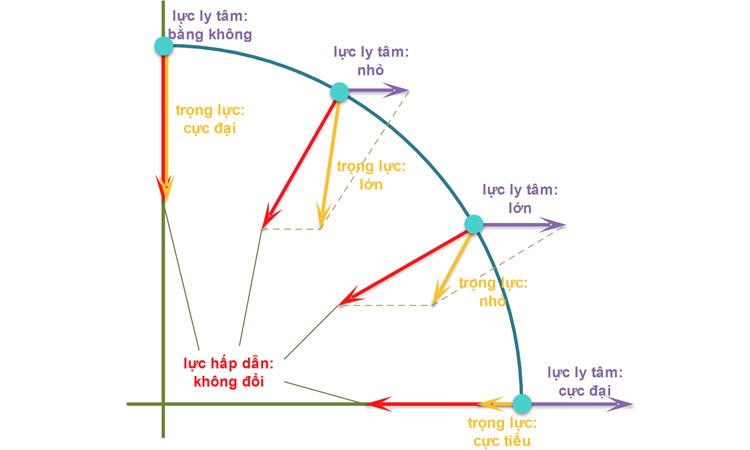
Kinh nghiệm cho thấy học sinh thường nhầm lẫn về mối quan hệ này. Tôi giải thích bằng ví dụ xe máy vào cua
- khi bán kính cua nhỏ, người lái phải giảm tốc để giảm lực li tâm, tránh nguy hiểm.
Việc hiểu rõ ba yếu tố trên giúp kiểm soát tốt lực li tâm trong các ứng dụng thực tế như thiết kế đường cua, máy ly tâm công nghiệp.
Ứng dụng của lực li tâm trong thực tế và kỹ thuật
Lực li tâm đóng vai trò quan trọng trong nhiều ứng dụng thực tiễn. Nguyên lý hoạt động của nó dựa trên sự chuyển động tròn tạo ra lực li tâm đẩy các vật ra xa tâm quay. Hiểu được nguyên lý này giúp chúng ta vận dụng hiệu quả trong công nghiệp và đời sống.

Máy ly tâm trong công nghiệp
Máy ly tâm được sử dụng rộng rãi trong các nhà máy sản xuất đường, dầu ăn và hóa chất. Nguyên lý hoạt động của máy dựa trên Công thức lực hồi phục để tách các thành phần có khối lượng riêng khác nhau.
Theo số liệu từ Viện Nghiên cứu Công nghiệp Việt Nam, máy ly tâm công nghiệp có thể đạt tốc độ quay lên đến 50.000 vòng/phút. Điều này cho phép tách các hỗn hợp phức tạp một cách nhanh chóng và hiệu quả.
Hiện tượng li tâm trong sinh hoạt
Khi giặt quần áo bằng máy giặt, giai đoạn vắt khô hoạt động dựa trên nguyên lý li tâm. Lồng giặt quay với tốc độ cao tạo ra lực đẩy nước ra khỏi quần áo qua các lỗ nhỏ.
Trong nhà bếp, máy xay sinh tố tận dụng lực li tâm để nghiền nhỏ thực phẩm. Lưỡi dao quay tốc độ cao tạo ra dòng xoáy, đẩy nguyên liệu va đập vào thành cối xay.
Ứng dụng trong các thiết bị kỹ thuật
Bơm li tâm được dùng phổ biến trong hệ thống cấp thoát nước. Cánh quạt bơm tạo ra lực li tâm đẩy chất lỏng di chuyển từ tâm ra ngoài với áp suất cao.
Trong động cơ ô tô, bộ điều tốc li tâm giúp điều chỉnh tốc độ động cơ. Khi tốc độ tăng, các quả nặng bị văng ra ngoài do lực li tâm, kéo theo cơ cấu giảm cung cấp nhiên liệu.
Máy điều hòa không khí cũng sử dụng quạt li tâm để tạo luồng gió mạnh. Thiết kế này giúp tăng hiệu suất làm mát và tiết kiệm năng lượng hơn so với quạt thông thường.
Bài tập và phương pháp giải về lực li tâm
Lực li tâm là một trong những khái niệm quan trọng trong vật lý. Công thức lực li tâm giúp ta tính toán được lực tác động lên vật chuyển động tròn đều.
Để giải các bài tập về lực li tâm, ta cần nắm vững công thức cơ bản và mối liên hệ với công thức lực lorenxo khi xét chuyển động của hạt tích điện.
Các dạng bài tập điển hình
Dạng 1: Tính lực li tâm tác dụng lên vật chuyển động tròn đều khi biết khối lượng, bán kính và vận tốc góc.
Dạng 2: Xác định vận tốc góc giới hạn để vật không bị văng ra khỏi quỹ đạo tròn.
Dạng 3: Tìm góc nghiêng của mặt đường vòng để xe không bị trượt khi chuyển động.
Phương pháp giải và mẹo làm bài
Bước 1: Xác định rõ các đại lượng đã cho trong đề bài và đại lượng cần tìm.
Bước 2: Vẽ sơ đồ lực tác dụng lên vật, chú ý chiều của các lực.

Kinh nghiệm của tôi cho thấy học sinh thường nhầm lẫn chiều của lực li tâm với lực hướng tâm.
Bước 3: Áp dụng định luật II Newton theo phương hướng tâm và phương tiếp tuyến.
Bài tập minh họa có lời giải chi tiết
Bài toán: Một ô tô khối lượng 1000kg chuyển động trên đường vòng bán kính 50m với vận tốc 36km/h. Tính lực li tâm tác dụng lên ô tô.
Lời giải:
- Đổi đơn vị: v = 36km/h = 10m/s
- Áp dụng công thức: F = mv²/R
- Thay số: F = 1000 × 100/50 = 2000N
Vậy lực li tâm tác dụng lên ô tô là 2000N, hướng ra phía ngoài đường tròn.
FAQ: Câu hỏi thường gặp về lực li tâm
Lực li tâm là một khái niệm quan trọng trong vật lý. Tôi sẽ giải đáp những thắc mắc phổ biến về lực li tâm mà học sinh thường gặp phải.
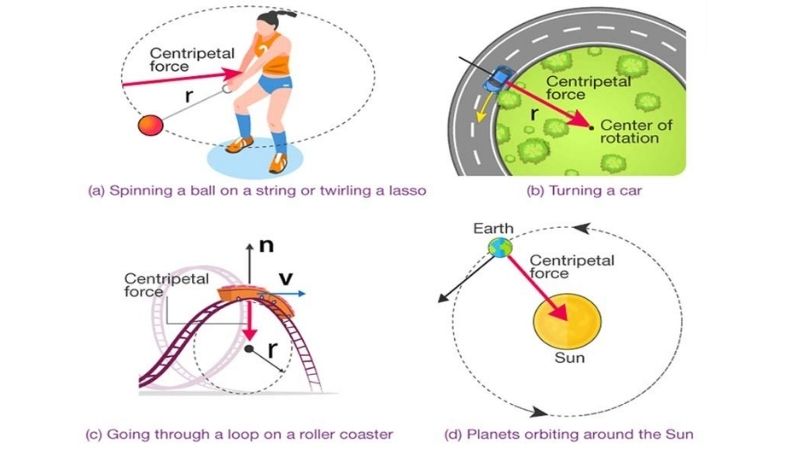
Sự khác biệt giữa lực li tâm và lực hướng tâm
Lực hướng tâm luôn hướng vào tâm chuyển động tròn và tạo ra chuyển động tròn của vật. Nó là lực thực tồn tại trong thực tế.
Ngược lại, lực li tâm là lực quán tính, chỉ xuất hiện trong hệ quy chiếu gắn với vật chuyển động tròn. Nó có phương, chiều ngược với lực hướng tâm.
Ví dụ khi xe ô tô vào cua, người ngồi trong xe cảm thấy bị đẩy ra ngoài do lực li tâm. Còn lực ma sát giữa bánh xe và mặt đường chính là lực hướng tâm.
Cách xác định chiều của lực li tâm
Chiều của lực li tâm luôn hướng ra xa tâm chuyển động tròn. Đây là quy tắc cơ bản giúp xác định nhanh chiều lực li tâm.
Trong quá trình giảng dạy, tôi thường ví von: “Lực li tâm giống như một đứa trẻ muốn thoát khỏi vòng tay mẹ khi bị xoay vòng”.
Khi giải bài tập, học sinh cần vẽ hình tròn chuyển động và xác định tâm trước. Sau đó vẽ véc tơ lực li tâm hướng thẳng ra ngoài từ vị trí vật.
Mối quan hệ giữa lực li tâm và gia tốc li tâm
Lực li tâm và gia tốc li tâm có mối quan hệ trực tiếp thông qua công thức:
F = ma
Trong đó:
- F là lực li tâm (N)
- m là khối lượng vật (kg)
- a là gia tốc li tâm (m/s2)
Gia tốc li tâm phụ thuộc vào vận tốc góc và bán kính quỹ đạo theo công thức:
a = ω2R
Với ω là vận tốc góc (rad/s) và R là bán kính quỹ đạo (m).
Việc áp dụng công thức lực li tâm đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống và kỹ thuật. Các yếu tố như khối lượng, vận tốc góc và bán kính quỹ đạo tác động trực tiếp đến độ lớn của lực li tâm. Kiến thức này giúp giải thích nhiều hiện tượng tự nhiên và ứng dụng trong máy móc công nghiệp. Thông qua các bài tập thực hành, học sinh nắm vững cách tính toán và vận dụng lực li tâm vào thực tế.
Bài viết liên quan

Kiến thức về công thức va chạm mềm và các định luật bảo toàn cơ bản
Tìm hiểu công thức va chạm mềm qua các khái niệm cơ bản, định luật bảo toàn và phương pháp giải bài tập chi tiết. Phân biệt va chạm đàn hồi, không đàn hồi với ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực cản không khí và ứng dụng thực tế
Tìm hiểu công thức tính lực cản không khí và các yếu tố ảnh hưởng trong chuyển động vật lý. Phân tích chi tiết cách áp dụng cho ô tô, xe máy kèm ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực hãm và ứng dụng trong vật lý cơ bản
Tìm hiểu chi tiết công thức tính lực hãm trong chuyển động, các thành phần cơ bản và ứng dụng thực tế. Hướng dẫn tính toán lực ma sát, lực cản môi trường và lực phản lực.

Tìm hiểu công thức tính gia tốc trung bình và ứng dụng thực tế
Tìm hiểu công thức tính gia tốc trung bình và các yếu tố ảnh hưởng trong chuyển động. Phân tích phương pháp tính cho từng dạng chuyển động kèm ứng dụng thực tế.

Nghiên cứu công thức định luật vạn vật hấp dẫn và ứng dụng thực tế
Tìm hiểu công thức định luật vạn vật hấp dẫn qua các thành phần cơ bản, mối quan hệ với trọng lực và phương pháp tính toán lực hấp dẫn giữa các vật trong thực tế.

Học công thức tính hiệu suất trong vật lý và các ứng dụng thực tế
Tìm hiểu công thức tính hiệu suất trong vật lý qua các khái niệm cơ bản, phương pháp tính toán cho bài toán cơ học và điện năng, kèm bài tập ví dụ chi tiết.

