Hiểu rõ công thức tính xung lượng và ứng dụng trong vật lý cơ bản
Công thức tính xung lượng là một trong những kiến thức nền tảng của vật lý. Các bài toán về xung lượng thường xuất hiện trong đề thi và kiểm tra. Bài viết trình bày chi tiết công thức, phương pháp giải và ứng dụng thực tế của xung lượng.
Công thức tính xung lượng trong vật lý
Xung lượng là đại lượng vật lý quan trọng mô tả động lượng của vật trong một khoảng thời gian. Công thức tính xung lượng được biểu diễn bằng tích của lực và thời gian tác dụng.

Công thức cơ bản:
I = F.Δt
Trong đó:
- I: Xung lượng (đơn vị: N.s)
- F: Lực tác dụng (đơn vị: N)
- Δt: Khoảng thời gian lực tác dụng (đơn vị: s)
Qua 20 năm giảng dạy, tôi nhận thấy học sinh thường nhầm lẫn giữa xung lượng và động lượng. Xung lượng chính là độ biến thiên động lượng của vật.
Mối liên hệ giữa xung lượng và động lượng:
I = Δp = p2
Trong đó:
- Δp: Độ biến thiên động lượng
- p2, p1: Động lượng cuối và đầu
- m: Khối lượng vật
- v2, v1: Vận tốc cuối và đầu
Ví dụ thực tế: Khi đấm boxing, võ sĩ thường ra đòn nhanh để tạo xung lượng lớn. Lực tác dụng trong thời gian ngắn sẽ tạo ra xung lượng đủ lớn để gây ảnh hưởng đến đối thủ.
Một mẹo nhỏ khi giải bài tập: Luôn xác định rõ chiều dương của chuyển động và áp dụng đúng dấu cho các đại lượng vận tốc, lực tác dụng để tránh sai sót khi tính toán.
Các thành phần cơ bản trong công thức xung lượng
Xung lượng là một đại lượng vật lý quan trọng trong cơ học. Nó mô tả sự tương tác giữa lực và thời gian tác dụng lên vật.
Công thức xung lượng được biểu diễn bằng tích của lực và khoảng thời gian tác dụng. Công thức này giúp ta hiểu được mối quan hệ giữa lực và sự thay đổi động lượng của vật.

Khái niệm về xung lượng và động lượng
Xung lượng là đại lượng véc tơ đặc trưng cho tác dụng của lực trong một khoảng thời gian nhất định. Nó được tính bằng công thức:
I = F.Δt
Trong đó:
- I là xung lượng
- F là lực tác dụng
- Δt là khoảng thời gian lực tác dụng
Động lượng là đại lượng véc tơ đặc trưng cho trạng thái chuyển động của vật. Mối liên hệ giữa xung lượng và động lượng được thể hiện qua công thức bảo toàn động lượng.
Mối quan hệ giữa lực và thời gian trong xung lượng
Lực và thời gian có mối quan hệ tỷ lệ thuận trong xung lượng. Khi tăng lực tác dụng, xung lượng sẽ tăng nếu thời gian giữ nguyên.
Ngược lại, ta có thể giảm lực tác dụng bằng cách tăng thời gian tương tác. Điều này giải thích tại sao võ sĩ thường “lướt theo” đòn đấm để giảm lực tác động.
Đơn vị đo xung lượng trong hệ SI
Trong hệ đơn vị SI, xung lượng được đo bằng đơn vị N.s (Newton.giây). Đây là tích của đơn vị lực (N) và đơn vị thời gian (s).
Ngoài ra, xung lượng còn có thể được biểu diễn bằng đơn vị kg.m/s, tương đương với đơn vị của động lượng. Điều này phản ánh mối liên hệ chặt chẽ giữa xung lượng và động lượng.
Việc nắm vững các đơn vị đo giúp học sinh tránh nhầm lẫn khi giải các bài toán liên quan đến xung lượng và động lượng.
Cách áp dụng công thức tính xung lượng trong các bài toán
Xung lượng là đại lượng vật lý quan trọng trong cơ học. Công thức tính xung lượng được áp dụng rộng rãi để giải các bài toán va chạm và chuyển động.

Khi giải bài tập về xung lượng, việc đầu tiên là xác định rõ các đại lượng đã cho trong đề bài. Sau đó áp dụng công thức p = mv để tính toán, trong đó p là xung lượng, m là khối lượng và v là vận tốc.
Một kinh nghiệm tôi thường chia sẻ với học sinh là vẽ sơ đồ lực tác dụng lên vật. Điều này giúp phân tích chính xác hướng của xung lượng và áp dụng định luật bảo toàn xung lượng.
Các dạng bài tập về xung lượng thường gặp
Qua nhiều năm giảng dạy, tôi nhận thấy có 3 dạng bài tập chính về xung lượng:
Dạng 1: Tính xung lượng của vật chuyển động thẳng đều. Đây là dạng cơ bản nhất, chỉ cần áp dụng trực tiếp công thức p = mv.
Dạng 2: Bài toán va chạm giữa hai vật. Cần vận dụng định luật bảo toàn xung lượng và phân tích các trường hợp va chạm đàn hồi hoặc không đàn hồi.
Dạng 3: Tính biến thiên xung lượng. Liên quan đến công thức tính momen quán tính khi vật chuyển động tròn.
Phương pháp giải bài tập xung lượng
Để giải thành công bài tập về xung lượng, cần tuân thủ các bước sau:
Bước 1: Đọc kỹ đề bài, ghi lại các đại lượng đã cho và cần tìm.
Bước 2: Vẽ sơ đồ lực tác dụng và xác định chiều dương.
Bước 3: Áp dụng công thức phù hợp và giải phương trình.
Bước 4: Kiểm tra đơn vị và độ hợp lý của kết quả.
Bài tập mẫu và hướng dẫn giải chi tiết
Bài tập: Một vật khối lượng 2kg chuyển động với vận tốc 5m/s. Tính xung lượng của vật.
Giải:
- Đại lượng đã cho: m = 2kg, v = 5m/s
- Áp dụng công thức: p = mv
- Thay số: p = 2 × 5 = 10 (kg.m/s)
- Đáp số: p = 10 kg.m/s
Lưu ý quan trọng khi giải bài tập: Đơn vị của xung lượng là kg.m/s, vector xung lượng cùng hướng với vector vận tốc.
Ứng dụng của xung lượng trong thực tế và kỹ thuật
Xung lượng đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống và kỹ thuật. Hiểu được công thức tính xung lượng giúp chúng ta giải quyết nhiều bài toán thực tiễn.
Việc áp dụng xung lượng trong thực tế đòi hỏi sự kết hợp với nhiều kiến thức khác như công thức tính momen ngẫu lực và ứng dụng định luật hooke.
Vai trò của xung lượng trong các va chạm
Va chạm là hiện tượng phổ biến trong tự nhiên và kỹ thuật. Xung lượng giúp đánh giá mức độ tác động trong va chạm giữa các vật.
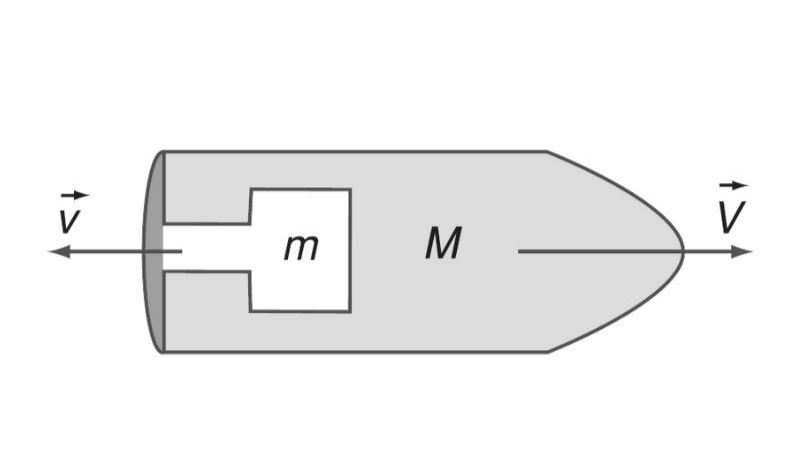
Trong thiết kế ô tô, các kỹ sư sử dụng nguyên lý xung lượng để tính toán vùng biến dạng. Điều này giúp bảo vệ người ngồi trong xe khi xảy ra tai nạn.
Theo nghiên cứu của Viện Khoa học Kỹ thuật Quốc gia Hoa Kỳ, việc áp dụng nguyên lý xung lượng trong thiết kế đã giảm 40% thương vong do tai nạn giao thông.
Ứng dụng trong công nghiệp và đời sống
Trong công nghiệp, xung lượng được ứng dụng rộng rãi trong các máy đóng cọc và búa thủy lực. Nguyên lý này giúp tăng hiệu quả công việc đáng kể.
Các nhà máy sản xuất ô tô sử dụng robot hàn điểm dựa trên nguyên lý xung lượng. Phương pháp này tạo ra mối hàn chắc chắn và tiết kiệm năng lượng.
Trong thể thao, huấn luyện viên áp dụng kiến thức về xung lượng để cải thiện kỹ thuật cho vận động viên. Đặc biệt trong các môn như quyền anh, bóng chày và golf.
FAQ: Câu hỏi thường gặp về xung lượng
Xung lượng là một khái niệm quan trọng trong vật lý. Tôi sẽ giải đáp những thắc mắc phổ biến về công thức xung lượng và các vấn đề liên quan.
Sự khác biệt giữa xung lượng và động lượng
Xung lượng là tích của lực và khoảng thời gian lực tác dụng. Còn động lượng là tích của khối lượng và vận tốc của vật.
Khi một lực tác dụng lên vật trong một khoảng thời gian, nó sẽ làm thay đổi động lượng của vật đó. Điều này được thể hiện qua định lý xung
- động lượng.
Trong thực tế, việc phân biệt hai khái niệm này rất quan trọng khi giải các bài toán va chạm. Ví dụ như công thức lực tương tác tĩnh điện sẽ tạo ra xung lượng khi hai điện tích tương tác.
Mối liên hệ giữa xung lượng và động năng
Xung lượng và động năng có mối quan hệ chặt chẽ thông qua công của lực. Khi lực tác dụng lên vật, nó sinh ra xung lượng.
Xung lượng này làm thay đổi vận tốc của vật. Sự thay đổi vận tốc dẫn đến biến thiên động năng theo công thức:
ΔEđ = (mv2²)/2
Trong quá trình giảng dạy, tôi thường lấy ví dụ về quả bóng tennis đập vào tường. Lực tác dụng trong thời gian ngắn tạo ra xung lượng lớn, làm thay đổi đáng kể động năng của quả bóng.

Các lỗi thường gặp khi tính xung lượng
Học sinh thường nhầm lẫn giữa lực trung bình và lực tức thời khi tính xung lượng. Lực trung bình được sử dụng khi lực thay đổi theo thời gian.
Một sai lầm khác là quên xét dấu của xung lượng. Dấu của xung lượng phụ thuộc vào chiều của lực tác dụng và phải được xét cẩn thận.
Kinh nghiệm của tôi cho thấy việc vẽ biểu đồ lực theo thời gian sẽ giúp học sinh hình dung rõ hơn về xung lượng và tránh được những sai sót phổ biến này.
Việc áp dụng công thức tính xung lượng đóng vai trò quan trọng trong nghiên cứu chuyển động và va chạm. Các thành phần cơ bản như lực, thời gian tác dụng và sự thay đổi động lượng tạo nên một hệ thống kiến thức chặt chẽ. Qua các bài tập mẫu và ứng dụng thực tế, công thức này giúp giải quyết nhiều vấn đề trong công nghiệp và đời sống. Kiến thức về xung lượng tạo nền tảng vững chắc cho việc học tập vật lý nâng cao.
Bài viết liên quan

Kiến thức về công thức va chạm mềm và các định luật bảo toàn cơ bản
Tìm hiểu công thức va chạm mềm qua các khái niệm cơ bản, định luật bảo toàn và phương pháp giải bài tập chi tiết. Phân biệt va chạm đàn hồi, không đàn hồi với ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực cản không khí và ứng dụng thực tế
Tìm hiểu công thức tính lực cản không khí và các yếu tố ảnh hưởng trong chuyển động vật lý. Phân tích chi tiết cách áp dụng cho ô tô, xe máy kèm ví dụ minh họa rõ ràng.

Điểm qua công thức tính lực hãm và ứng dụng trong vật lý cơ bản
Tìm hiểu chi tiết công thức tính lực hãm trong chuyển động, các thành phần cơ bản và ứng dụng thực tế. Hướng dẫn tính toán lực ma sát, lực cản môi trường và lực phản lực.

Tìm hiểu công thức tính gia tốc trung bình và ứng dụng thực tế
Tìm hiểu công thức tính gia tốc trung bình và các yếu tố ảnh hưởng trong chuyển động. Phân tích phương pháp tính cho từng dạng chuyển động kèm ứng dụng thực tế.

Nghiên cứu công thức định luật vạn vật hấp dẫn và ứng dụng thực tế
Tìm hiểu công thức định luật vạn vật hấp dẫn qua các thành phần cơ bản, mối quan hệ với trọng lực và phương pháp tính toán lực hấp dẫn giữa các vật trong thực tế.

Học công thức tính hiệu suất trong vật lý và các ứng dụng thực tế
Tìm hiểu công thức tính hiệu suất trong vật lý qua các khái niệm cơ bản, phương pháp tính toán cho bài toán cơ học và điện năng, kèm bài tập ví dụ chi tiết.

