Công thức va chạm đàn hồi và ứng dụng trong giải bài tập vật lý

Công thức va chạm đàn hồi mô tả quá trình bảo toàn động lượng và động năng giữa các vật. Các phương trình toán học này giúp dự đoán chuyển động của vật sau va chạm. Bài viết phân tích chi tiết các trường hợp va chạm đàn hồi phổ biến trong thực tế.

Công thức va chạm đàn hồi là gì?

Công thức va chạm đàn hồi là phương trình mô tả sự bảo toàn động lượng và động năng trong quá trình va chạm giữa hai vật. Đây là trường hợp lý tưởng khi không có sự mất mát năng lượng.

Công thức tổng quát được biểu diễn:

m1v1 + m2v2 = m1v1′ + m2v2′
(Phương trình bảo toàn động lượng)

1/2m1v1² + 1/2m2v2² = 1/2m1v1’² + 1/2m2v2’²
(Phương trình bảo toàn động năng)

Trong đó:

• m1, m2: Khối lượng của vật 1 và vật 2
• v1, v2: Vận tốc ban đầu của vật 1 và vật 2
• v1′, v2′: Vận tốc sau va chạm của vật 1 và vật 2

Qua 20 năm giảng dạy, tôi thường ví von va chạm đàn hồi như hai quả bóng cao su va vào nhau rồi bật ra. Chúng không bị biến dạng và không mất năng lượng.

Một mẹo nhỏ để nhớ: Tổng động lượng và động năng trước va chạm luôn bằng tổng động lượng và động năng sau va chạm. Giống như việc bạn đếm tiền trước và sau khi cho vay

• số tiền phải bằng nhau.

Áp dụng công thức này giúp giải quyết nhiều bài toán về va chạm trong vật lý. Đặc biệt khi xét các vật chuyển động trên mặt phẳng ngang không ma sát.

Các điều kiện và đặc điểm của va chạm đàn hồi

Va chạm đàn hồi là một hiện tượng phổ biến trong cơ học. Khi hai vật va chạm với nhau, chúng có thể biến dạng tạm thời rồi khôi phục lại hình dạng ban đầu.

Trong quá trình giảng dạy, tôi thường lấy ví dụ về quả bóng tennis nảy trên sân. Khi va chạm với mặt sân, quả bóng bị biến dạng nhẹ rồi nảy lên gần như không mất năng lượng.

Công thức va chạm đàn hồi được áp dụng khi hai vật tương tác theo định luật bảo toàn động lượng và cơ năng. Để hiểu rõ hơn về va chạm không đàn hồi, bạn có thể tham khảo thêm về công thức va chạm mềm.

Định nghĩa và đặc trưng của va chạm đàn hồi

Va chạm đàn hồi là va chạm mà sau khi va chạm, các vật khôi phục hoàn toàn hình dạng ban đầu. Trong va chạm này không có sự mất mát cơ năng.

Đặc trưng quan trọng nhất là hệ số va chạm e = 1. Điều này có nghĩa tốc độ tương đối của hai vật sau va chạm bằng tốc độ tương đối trước va chạm nhưng ngược chiều.

Một ví dụ điển hình là va chạm giữa các phân tử khí trong bình kín. Các phân tử va chạm với nhau và với thành bình theo quy luật đàn hồi hoàn toàn.

Các định luật bảo toàn trong va chạm đàn hồi

Trong va chạm đàn hồi, hai định luật bảo toàn cơ bản luôn được thỏa mãn:

Định luật bảo toàn động lượng:

m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂

Định luật bảo toàn cơ năng:

½m₁v₁² + ½m₂v₂² = ½m₁u₁² + ½m₂u₂²

Trong đó:

• m₁, m₂: khối lượng của hai vật
• v₁, v₂: vận tốc trước va chạm
• u₁, u₂: vận tốc sau va chạm

Phân biệt va chạm đàn hồi và không đàn hồi

Va chạm đàn hồi và không đàn hồi có những điểm khác biệt cơ bản. Va chạm đàn hồi bảo toàn cả động lượng và cơ năng, các vật khôi phục hình dạng ban đầu.

Ngược lại, va chạm không đàn hồi chỉ bảo toàn động lượng. Một phần cơ năng chuyển hóa thành nhiệt năng và năng lượng biến dạng.

Trong thực tế, hầu hết các va chạm đều là va chạm không hoàn toàn đàn hồi. Tuy nhiên, nhiều trường hợp có thể xem xấp xỉ là va chạm đàn hồi để đơn giản hóa bài toán.

Công thức va chạm đàn hồi xuyên tâm và ứng dụng

Va chạm đàn hồi xuyên tâm là hiện tượng hai vật va chạm theo đường thẳng đi qua trọng tâm của chúng. Trong quá trình này, động năng được bảo toàn hoàn toàn.

Khi nghiên cứu công thức va chạm đàn hồi xuyên tâm, chúng ta cần xét đến hai phương trình cơ bản. Đó là phương trình động lượng và phương trình động năng.

Tương tự như công thức dung kháng, các công thức này giúp giải quyết nhiều bài toán phức tạp trong vật lý.

Phương trình động lượng trong va chạm xuyên tâm

Phương trình động lượng thể hiện định luật bảo toàn động lượng trong va chạm:

m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂

Trong đó:

• m₁, m₂: khối lượng của vật 1 và vật 2
• v₁, v₂: vận tốc ban đầu của vật 1 và vật 2
• u₁, u₂: vận tốc sau va chạm của vật 1 và vật 2

Kinh nghiệm giảng dạy cho thấy học sinh thường nhầm lẫn dấu của vận tốc. Cần chú ý quy ước chiều dương trước khi giải.

Phương trình động năng trong va chạm xuyên tâm

Va chạm đàn hồi tuân theo định luật bảo toàn động năng:

½m₁v₁² + ½m₂v₂² = ½m₁u₁² + ½m₂u₂²

Phương trình này thể hiện tổng động năng trước và sau va chạm bằng nhau. Không có năng lượng bị mất đi dưới dạng nhiệt hoặc biến dạng.

Từ hai phương trình trên, ta có thể tính được vận tốc của các vật sau va chạm.

Bài tập minh họa về va chạm đàn hồi xuyên tâm

Bài tập: Hai vật khối lượng m₁ = 2kg và m₂ = 3kg chuyển động ngược chiều với vận tốc v₁ = 3m/s và v₂ = -2m/s. Tính vận tốc của chúng sau va chạm.

Giải:

• Áp dụng phương trình động lượng:

2(3) + 3(-2) = 2u₁ + 3u₂
6

• 6 = 2u₁ + 3u₂ (1)

• Áp dụng phương trình động năng:

½(2)(3)² + ½(3)(-2)² = ½(2)u₁² + ½(3)u₂²
9 + 6 = u₁² + 1.5u₂² (2)

Từ (1) và (2) ta tìm được: u₁ = -2m/s và u₂ = 2m/s

Phân tích chuyển động và năng lượng trong va chạm đàn hồi

Va chạm đàn hồi là hiện tượng hai vật va chạm vào nhau mà không mất năng lượng cơ học. Các vật sau va chạm sẽ tách rời nhau và giữ nguyên hình dạng ban đầu.

Trong công thức va chạm đàn hồi, tổng động lượng và động năng của hệ được bảo toàn. Điều này giúp ta dễ dàng tính toán các đại lượng sau va chạm.

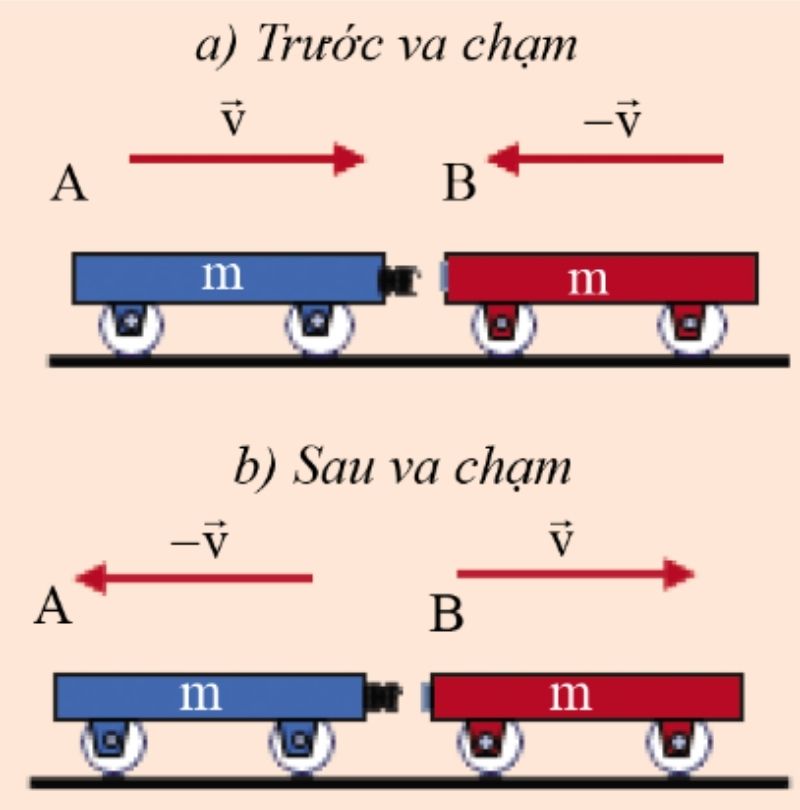
Khi giảng dạy, tôi thường lấy ví dụ về hai viên bi ve sáng bóng va chạm nhau. Học sinh sẽ thấy rõ chúng bật ra sau va chạm mà không bị biến dạng.

Mối quan hệ giữa vận tốc trước và sau va chạm

Trong va chạm đàn hồi một chiều, vận tốc tương đối của hai vật trước và sau va chạm bằng nhau về độ lớn nhưng ngược chiều:

v1′

• v2′ = -(v1 - v2)

Với v1, v2 là vận tốc trước va chạm và v1′, v2′ là vận tốc sau va chạm. Công thức này rất quan trọng để giải các bài tập va chạm.

Sự biến đổi động năng trong va chạm đàn hồi

Động năng của hệ được bảo toàn trong va chạm đàn hồi. Tổng động năng trước va chạm bằng tổng động năng sau va chạm:

1/2m1v1² + 1/2m2v2² = 1/2m1v1’² + 1/2m2v2’²

Khi giải bài tập, ta có thể kết hợp phương trình này với định luật bảo toàn động lượng để tìm vận tốc sau va chạm.

Thế năng đàn hồi và sự chuyển hóa năng lượng

Công thức tính thế năng đàn hồi cho thấy năng lượng được tích trữ khi vật biến dạng đàn hồi:

W = 1/2kx²

Trong đó k là độ cứng của lò xo và x là độ biến dạng. Thế năng này sẽ chuyển hóa thành động năng khi vật bật ra.

Quá trình chuyển hóa năng lượng diễn ra rất nhanh. Thế năng đàn hồi cực đại khi vật biến dạng nhiều nhất và chuyển hoàn toàn thành động năng khi vật bật ra.

Ứng dụng công thức va chạm đàn hồi trong thực tế

Va chạm đàn hồi là hiện tượng phổ biến trong cuộc sống. Các vật sau va chạm vẫn giữ nguyên động năng ban đầu và không bị biến dạng.

Hiểu được nguyên lý va chạm đàn hồi giúp chúng ta ứng dụng hiệu quả trong nhiều lĩnh vực khác nhau. Đặc biệt là trong thể thao và công nghiệp.

Va chạm đàn hồi trong các môn thể thao

Bóng bàn là môn thể thao điển hình ứng dụng va chạm đàn hồi. Khi bóng va chạm với vợt, động năng được bảo toàn giúp bóng nảy đi xa.

Trong tennis, các cây vợt được thiết kế với độ đàn hồi cao. Điều này giúp tăng tốc độ và lực đánh bóng khi va chạm.

Theo nghiên cứu của Viện Khoa học Thể thao Mỹ, bóng billiard va chạm với băng bàn có hệ số đàn hồi tới 0.95. Đây là yếu tố quan trọng tạo nên những cú đánh chính xác.

Va chạm đàn hồi trong công nghiệp và kỹ thuật

Các lò xo giảm xóc ô tô hoạt động dựa trên nguyên lý va chạm đàn hồi. Chúng hấp thụ và giải phóng năng lượng khi xe di chuyển.

Trong ngành sản xuất đồ chơi, các vật liệu cao su và nhựa đàn hồi được sử dụng phổ biến. Chúng tạo ra các sản phẩm an toàn và bền bỉ cho trẻ em.

Khi thiết kế máy móc, kỹ sư thường tính toán công thức dao động cưỡng bức kết hợp với va chạm đàn hồi. Điều này giúp tối ưu hiệu suất và tuổi thọ thiết bị.

Bài tập thực hành về va chạm đàn hồi

Để hiểu rõ va chạm đàn hồi, học sinh có thể thực hiện thí nghiệm đơn giản. Thả quả bóng tennis từ độ cao khác nhau và đo độ nảy.

Một bài tập khác là quan sát va chạm giữa hai viên bi. Đặt chúng trên mặt phẳng ngang và cho va chạm với vận tốc khác nhau.

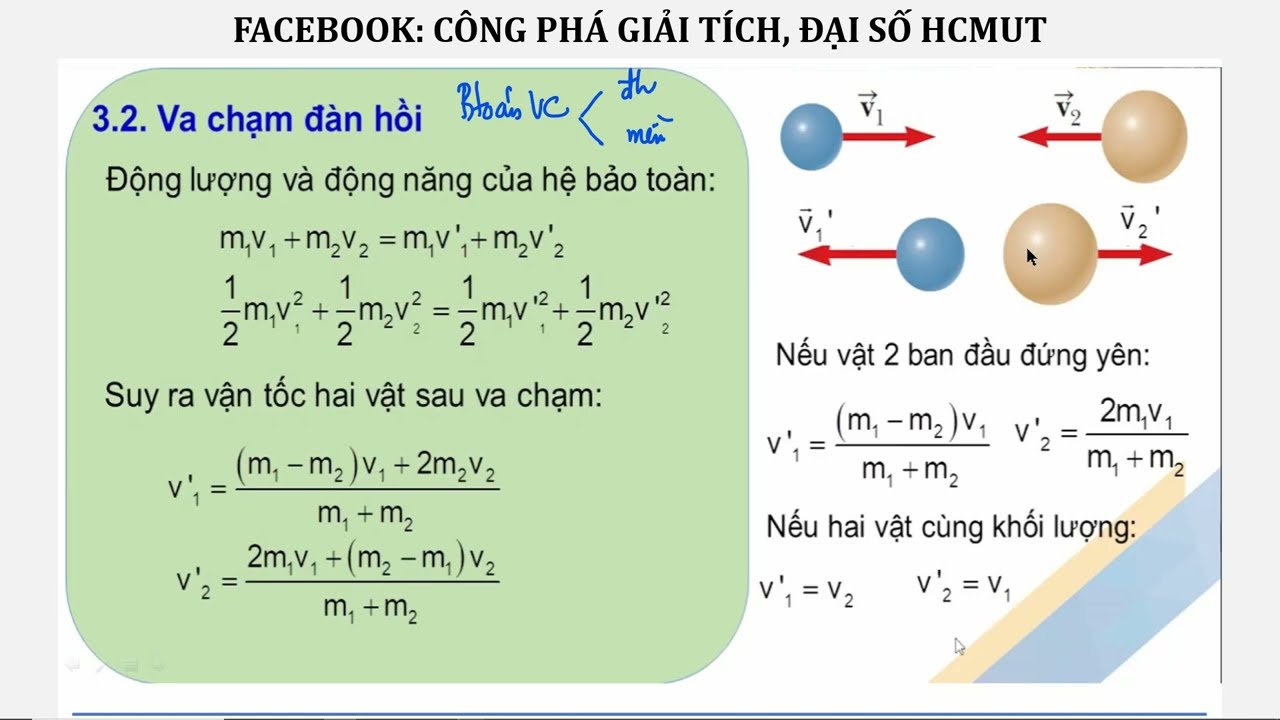
Qua 20 năm giảng dạy, tôi nhận thấy học sinh hiểu sâu hơn khi được thực hành. Các em cần ghi chép và so sánh kết quả thực tế với lý thuyết.

FAQ: Câu hỏi thường gặp về va chạm đàn hồi

Các câu hỏi thường gặp về va chạm đàn hồi giúp học sinh hiểu rõ hơn về hiện tượng vật lý này. Tôi sẽ giải đáp những thắc mắc phổ biến nhất mà học sinh hay gặp phải.

Sự khác biệt giữa va chạm đàn hồi và va chạm không đàn hồi?

Va chạm đàn hồi bảo toàn cả động năng và động lượng của hệ. Các vật sau va chạm không bị biến dạng và không mất năng lượng.

Va chạm không đàn hồi chỉ bảo toàn động lượng, một phần động năng chuyển thành nhiệt năng và năng lượng biến dạng. Các vật có thể bị méo mó hoặc vỡ.

Ví dụ điển hình là quả bóng cao su nảy trên sàn là va chạm đàn hồi, còn quả trứng rơi vỡ là va chạm không đàn hồi.

Làm thế nào để xác định hệ số va chạm?

Hệ số va chạm k được tính bằng tỷ số giữa vận tốc tương đối sau và trước va chạm:

k = |v’2

• v’1|/|v2 - v1|

Trong đó:

• v’1, v’2 là vận tốc của vật 1, vật 2 sau va chạm
• v1, v2 là vận tốc của vật 1, vật 2 trước va chạm

Với va chạm đàn hồi hoàn toàn, k = 1
Với va chạm không đàn hồi hoàn toàn, k = 0

Các lỗi thường gặp khi giải bài tập va chạm đàn hồi?

Qua nhiều năm giảng dạy, tôi nhận thấy học sinh thường mắc phải những sai lầm cơ bản sau:

Nhầm lẫn chiều dương và âm khi viết phương trình động lượng. Cần xác định rõ chiều dương ngay từ đầu bài.

Quên kiểm tra điều kiện bảo toàn động năng. Va chạm đàn hồi phải thỏa mãn cả hai định luật bảo toàn.

Áp dụng sai công thức hệ số va chạm. Cần chú ý dấu của vận tốc và thứ tự các vật trong công thức.

Việc áp dụng công thức va chạm đàn hồi đóng vai trò quan trọng trong nghiên cứu chuyển động của vật chất. Các phương trình động lượng và động năng giúp giải thích chính xác quá trình va chạm giữa các vật. Định luật bảo toàn động lượng và năng lượng là nền tảng để phân tích va chạm đàn hồi xuyên tâm. Kiến thức này có ứng dụng rộng rãi trong thể thao, công nghiệp và đời sống hàng ngày.