Nắm kỹ công thức bảo toàn động lượng và ứng dụng trong vật lý 10

Công thức bảo toàn động lượng là nguyên lý cơ bản trong vật lý. Nó mô tả sự tương tác giữa các vật trong hệ kín. Công thức này giúp giải quyết các bài toán va chạm và phản ứng. Học sinh cần nắm vững điều kiện áp dụng và phương pháp giải phù hợp.

Công thức bảo toàn động lượng là gì?

Công thức bảo toàn động lượng là một định luật vật lý quan trọng mô tả sự bảo toàn động lượng trong hệ kín. Nó thể hiện tổng động lượng của hệ trước và sau va chạm là không đổi.

Công thức được biểu diễn như sau:

m1v1 + m2v2 = m1v1′ + m2v2′

Trong đó:

• m1, m2: Khối lượng của vật 1 và vật 2
• v1, v2: Vận tốc của vật 1 và vật 2 trước va chạm
• v1′, v2′: Vận tốc của vật 1 và vật 2 sau va chạm

Khi giảng dạy, tôi thường lấy ví dụ về trò chơi bi-a để học sinh dễ hình dung. Khi quả bi trắng va chạm vào quả bi màu, tổng động lượng của hai quả bi trước và sau va chạm luôn bằng nhau.

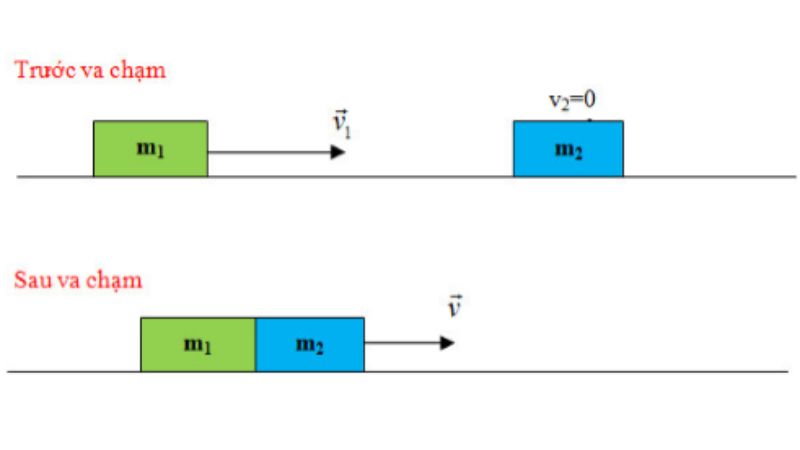
Một lưu ý quan trọng khi áp dụng công thức là phải xác định chiều dương và âm của vận tốc. Vận tốc cùng chiều với chiều dương thì mang dấu dương và ngược lại.

Để giải các bài tập về bảo toàn động lượng, học sinh cần:

• Xác định rõ hệ vật trước và sau va chạm
• Chọn chiều dương phù hợp
• Thay số đúng đơn vị vào công thức
• Kiểm tra kết quả có hợp lý không

Việc nắm vững công thức này giúp giải quyết nhiều bài toán về va chạm trong cơ học.

Nội dung và ý nghĩa của định luật bảo toàn động lượng

Công thức định luật bảo toàn động lượng là một trong những định luật quan trọng nhất của vật lý. Nó mô tả sự bảo toàn của tổng động lượng trong một hệ kín.

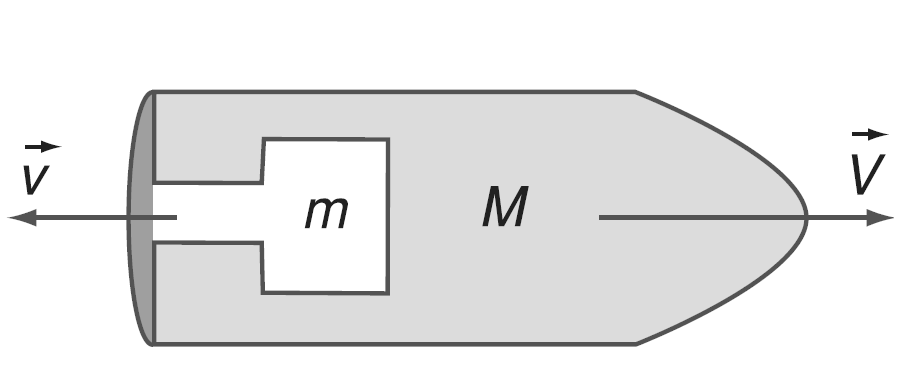
Định luật này giúp chúng ta hiểu và giải thích nhiều hiện tượng trong tự nhiên. Từ việc phóng tên lửa đến va chạm giữa các vật thể đều tuân theo nguyên lý này.

Để hiểu rõ hơn về định luật này, chúng ta cần nắm vững các khía cạnh cơ bản sau đây. Định luật này có mối liên hệ mật thiết với công thức định luật bảo toàn cơ năng.

Phát biểu định luật bảo toàn động lượng

Trong một hệ cô lập, tổng động lượng của hệ luôn được bảo toàn. Điều này có nghĩa là tổng vector động lượng trước và sau tương tác là không đổi.

Công thức toán học thể hiện định luật:

P1 + P2 = P’1 + P’2

Trong đó:

• P1, P2: Động lượng của các vật trước tương tác
• P’1, P’2: Động lượng của các vật sau tương tác

Điều kiện áp dụng định luật

Để áp dụng định luật bảo toàn động lượng, hệ vật cần thỏa mãn hai điều kiện cơ bản:

Hệ phải là hệ cô lập, không chịu tác động của ngoại lực. Điều này đảm bảo không có sự trao đổi động lượng với môi trường bên ngoài.

Các lực tương tác giữa các vật trong hệ phải là lực trong. Các lực này xuất hiện theo cặp và tuân theo định luật III Newton.

Các dạng biểu diễn của công thức

Công thức có thể được biểu diễn theo nhiều cách khác nhau tùy bài toán:

m1v1 + m2v2 = m1v’1 + m2v’2

Với m là khối lượng và v là vận tốc của vật.

Trong trường hợp va chạm một chiều:

m1v1 + m2v2 = m1v’1 + m2v’2

Với các đại lượng vô hướng theo phương chuyển động.

Kinh nghiệm giảng dạy cho thấy học sinh thường dễ nhớ công thức khi liên hệ với các ví dụ thực tế như phản lực của súng khi bắn đạn hoặc va chạm giữa các viên bi.

Hướng dẫn áp dụng công thức bảo toàn động lượng lớp 10

Định luật bảo toàn động lượng là một trong những định luật quan trọng trong vật lý. Tôi sẽ giúp các em nắm vững công thức định luật bảo toàn động lượng lớp 10 một cách dễ hiểu nhất.

Công thức cơ bản:

p₁ + p₂ = p’₁ + p’₂

Trong đó:

• p₁, p₂: động lượng của vật 1 và vật 2 trước va chạm
• p’₁, p’₂: động lượng của vật 1 và vật 2 sau va chạm

Các bước giải bài tập

Bước 1: Xác định các đại lượng đã cho trong đề bài như khối lượng và vận tốc của các vật.

Bước 2: Viết công thức tổng quát:
m₁v₁ + m₂v₂ = m₁v’₁ + m₂v’₂

Bước 3: Thay số và giải phương trình để tìm đại lượng cần tìm.

Kinh nghiệm của tôi khi giảng dạy cho thấy học sinh thường nhầm lẫn dấu của vận tốc. Các em cần chú ý chiều dương đã chọn để xác định dấu chính xác.

Ví dụ minh họa

Một viên bi khối lượng 100g chuyển động với vận tốc 2m/s va chạm vào viên bi khối lượng 200g đang đứng yên. Sau va chạm, viên bi thứ nhất chuyển động ngược lại với vận tốc 1m/s.

Áp dụng công thức bảo toàn động lượng:
0,1 × 2 + 0,2 × 0 = 0,1 × (-1) + 0,2 × v₂
⇒ v₂ = 1,5 m/s

Lưu ý khi sử dụng công thức

Khi áp dụng định luật bảo toàn động lượng, cần đặc biệt chú ý:

Chỉ áp dụng cho hệ kín không chịu tác dụng của ngoại lực.

Phải xác định rõ chiều dương để gán dấu cho vận tốc chính xác.

Đơn vị của các đại lượng phải thống nhất trong hệ SI.

Tôi thường nhắc học sinh kiểm tra kết quả bằng cách thay ngược lại vào công thức ban đầu để tránh sai sót không đáng có.

Các dạng bài tập thường gặp về bảo toàn động lượng

Định luật công thức bảo toàn động lượng là nền tảng quan trọng để giải các bài tập va chạm và phản ứng trong vật lý. Tôi sẽ phân tích chi tiết từng dạng bài tập phổ biến để các em nắm vững cách áp dụng.

Bài tập va chạm đàn hồi

Va chạm đàn hồi là trường hợp động năng được bảo toàn hoàn toàn. Khi hai vật va chạm, chúng sẽ bật ra với vận tốc mới.

Công thức cần nhớ:

m1v1 + m2v2 = m1v1′ + m2v2′
m1v1² + m2v2² = m1v1’² + m2v2’²

Trong đó m là khối lượng, v là vận tốc ban đầu, v’ là vận tốc sau va chạm. Tôi thường hướng dẫn học sinh giải theo 3 bước: viết phương trình bảo toàn động lượng, viết phương trình bảo toàn động năng và giải hệ phương trình.

Bài tập va chạm không đàn hồi

Với va chạm không đàn hồi, một phần động năng bị mất đi do biến dạng vật liệu. Hai vật sẽ dính vào nhau sau va chạm.

Phương trình cơ bản:

m1v1 + m2v2 = (m1 + m2)v
v = (m1v1 + m2v2)/(m1 + m2)

Kinh nghiệm của tôi là nên vẽ sơ đồ trước và sau va chạm để hình dung rõ quá trình. Điều này giúp học sinh không bị nhầm lẫn khi áp dụng công thức.

Bài tập phản ứng và phân rã

Phản ứng và phân rã là các quá trình một vật tách thành nhiều vật hoặc nhiều vật kết hợp thành một vật mới.

Với bài tập phân rã:

mv = m1v1 + m2v2
v = 0 (nếu vật đứng yên ban đầu)

Với bài tập phản ứng:
m1v1 + m2v2 = mv
v = (m1v1 + m2v2)/m

Tôi thường gợi ý học sinh xác định rõ trạng thái trước và sau phản ứng, từ đó áp dụng đúng dấu của các đại lượng trong công thức.

FAQ: Câu hỏi thường gặp về công thức bảo toàn động lượng

Trong quá trình giảng dạy, tôi nhận thấy học sinh thường gặp nhiều thắc mắc về công thức bảo toàn động lượng. Sau đây là những câu hỏi phổ biến nhất và cách giải đáp chi tiết.

Phân biệt va chạm đàn hồi và không đàn hồi

Va chạm đàn hồi là quá trình hai vật va chạm mà động năng được bảo toàn hoàn toàn. Các vật sau va chạm tách rời nhau với vận tốc xác định.

Va chạm không đàn hồi xảy ra khi hai vật dính vào nhau sau va chạm. Một phần động năng chuyển thành nhiệt năng và biến dạng.

Ví dụ thực tế: Khi hai viên bi ve sáng bóng va chạm là va chạm đàn hồi. Còn hai viên đất sét va chạm rồi dính vào nhau là va chạm không đàn hồi.

Mối liên hệ với các định luật bảo toàn khác

Định luật bảo toàn động lượng luôn đúng trong mọi va chạm, dù đàn hồi hay không đàn hồi. Nó có mối liên hệ chặt chẽ với định luật bảo toàn năng lượng.

Trong va chạm đàn hồi, cả động lượng và động năng đều được bảo toàn. Điều này giúp ta có thêm phương trình để giải bài toán.

Với va chạm không đàn hồi, chỉ có động lượng được bảo toàn. Động năng sau va chạm luôn nhỏ hơn trước va chạm.

Các sai lầm thường gặp khi áp dụng

Sai lầm phổ biến nhất là quên xét chiều của vận tốc. Vận tốc là đại lượng véc tơ nên cần chú ý dấu dương/âm.

Một số học sinh áp dụng nhầm công thức bảo toàn động năng cho va chạm không đàn hồi. Điều này dẫn đến kết quả sai.

Kinh nghiệm của tôi là nên vẽ sơ đồ chuyển động trước khi giải. Điều này giúp xác định đúng chiều vận tốc và loại va chạm.

Việc áp dụng công thức bảo toàn động lượng đóng vai trò quan trọng trong giải các bài tập cơ học. Định luật này giúp giải quyết nhiều dạng bài tập về va chạm, phản ứng và phân rã vật chất. Các học sinh cần nắm vững điều kiện áp dụng và phương pháp giải từng dạng bài tập cụ thể. Đặc biệt phải phân biệt rõ va chạm đàn hồi và không đàn hồi để áp dụng công thức chính xác.