Công thức tính chu kỳ chuyển động điều hòa, tròn đều chi tiết

Tổng hợp công thức tính chu kỳ chuyển động điều hòa, chuyển động tròn đều, chu kỳ lò xo, con lắc đơn,.. khoa học và dễ hiểu. Cùng nằm lòng lý thuyết và thực hành bằng cách giải các bài tập kèm lời giải chuẩn xác.

Chu kỳ là gì?

Chu kỳ là thời gian giữa hai lần lặp lại liên tiếp của một sự việc hoặc kết thúc của một chu trình, vòng quay. Đơn vị của chu kỳ thường là giây (s).

Trong vật lý, có hai loại chu kỳ thường gặp:

• Chu kỳ chuyển động tròn đều là thời gian để vật đi được một vòng.
• Chu kỳ của giao động điều hòa là khoảng thời gian ngắn nhất để lặp lại trạng thái của vật.

Công thức tính chu kỳ

Tổng hợp các công thức tính chu kỳ của các loại giao động phổ biến nhất hiện nay: dao động điều hòa, dao động tròn đều, dao động của con lắc đơn, con lắc lò xo,.. Tham khảo cách thức tính chuẩn xác dưới đây:

1/ Công thức tính chu kì dao động điều hòa

T = 1/f

Trong đó:

• T là chu kỳ của dao động điều hòa
• f là tần số của giao động

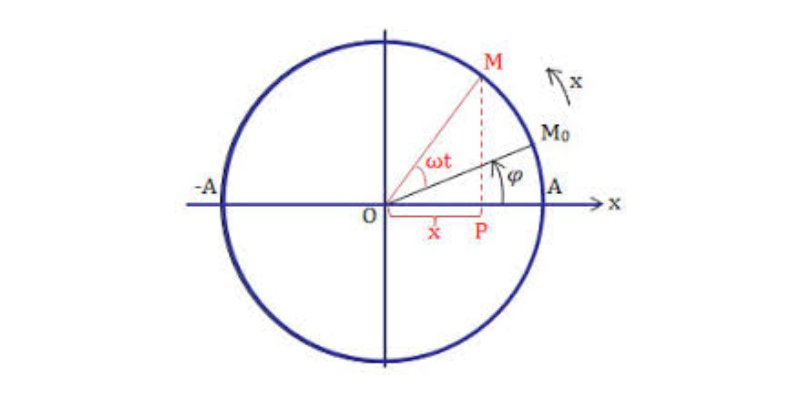
2/ Công thức tính chu kì chuyển động tròn đều

T = 2π/w = 1/f = 1/n = 2πr/v

Trong đó:

• T là chu kỳ của chuyển động tròn đều
• v là tốc độ
• r là bán kính của đường tròn
• w là tốc độ góc
• f là tần số chuyển động

3/ Công thức tính chu kỳ của con lắc lò xo

T = 2π√(m/k)

Trong đó:

• T là chu kỳ của con lắc lò xo
• k là độ cứng của lò xo
• m là khối lượng của lò xo

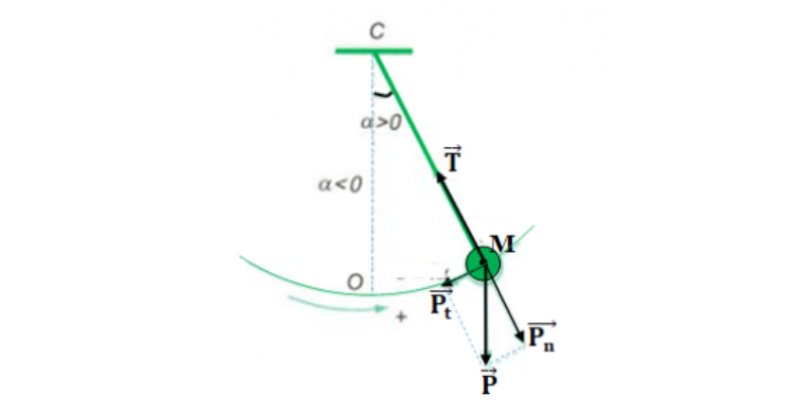
4/ Công thức tính chu kỳ của con lắc đơn

T = 2π√(l/g)

Trong đó:

• T là chu kỳ của con lắc đơn
• l là độ dài sợi dây của con lắc
• g là gia tốc trọng trường tại nơi treo con lắc

Bài tập vận dụng công thức chu kì

Dưới đây là tổng hợp các bài tập công thức chu kỳ hay nhất, giúp bạn test lại khả năng hiểu bài của bản thân. Tham khảo lời giải để hiểu cách giải và khắc phục những sai sót trong quá trình làm đề.

Bài tập 1

Một vật điểm chuyển động trên đường tròn bán kính 10cm với tần số không đổi 10 vòng/s. Tính chu kì, tần số góc, tốc độ dài.

Bài giải:

Theo đề bài, ta có:  f = 10 vòng/s  ( Hz)

Ta có: ω = 2πf = 20π rad/s

Chu kỳ T = 1/f = 0,1s

Vận tốc dài: v = r.ω = 6,283 m/s

Bài tập 2

Một con lắc lò xo nằm ngang có độ cứng K = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1kg. Kích thích cho vật dao động điều hòa, xác định chu kỳ của con lắc lò xo? Lấy π2 = 10.

Bài giải:

Quy đổi: M = 100g = 0,1 kg

Chu kỳ của con lắc lò xo là: T =2π√(m/k)

=> T = 2π√(0.1/100)

=> T = 2 s

Bài tập 3

Một đĩa quay đều quanh trục qua tâm O, với vận tốc qua tâm là 300 vòng/ phút. Tính tốc độ góc, chu kì.

Bài giải:

Quy đổi: f = 300 vòng/phút = 5 vòng/s

Tốc độ góc của đĩa quay là: ω = 2π.f = 10π rad/s

Chu kỳ của đĩa quay là: T = 1/f = 0.2 s

Bài tập 4

Một con lắc lò xo có độ cứng là K, Một đầu gắn cố định, một đầu gắn với vật nặng có khối lượng m. Kích thích cho vật dao động, nó dao động điều hòa với chu kỳ là T. Hỏi nếu tăng gấp đôi khối lượng của vật và giảm độ cứng đi 2 lần thì chu kỳ của con lắc lò xo sẽ thay đổi như thế nào?

1. Không đổi      B. Tăng lên 2 lần       C.Giảm đi 2 lần      D. Giảm 4 lần

Bài giải:

Gọi chu kỳ ban đầu của con lắc lò xo là: T =2π√(m/k)

Goị T’ là chu kỳ của con lắc sau khi thay đổi khối lượng và độ cứng của lò xo.

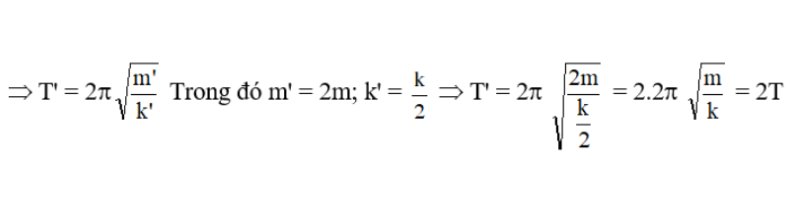
Bài tập 5

Một lò xo có độ cứng là K. Khi gắn vật m₁ vào lò xo và cho dao động thì chu kỳ dao động là 0,3s. Khi gắn vật có khối lượng m₂ vào lò xo trên và kích thích cho dao động thì nó dao động với chu kỳ là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m₁ + 3m₂ thì nó dao động với chu kỳ là bao nhiêu?

1. 0,25s            B. 0,4s                C. 0,812s               D. 0,3s

Bài giải:

Xác định chu kỳ dao động của vật khi gắn vật có khối lượng m = a. m₁ + b. m₂

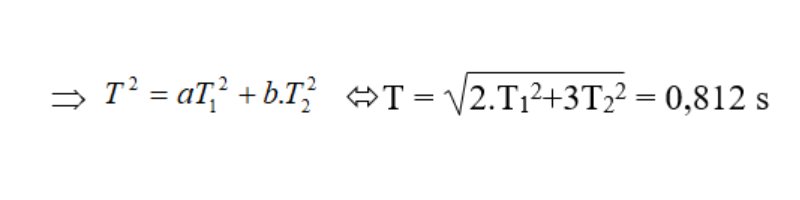
Bài tập 6:

Một vật nhỏ treo vào một lò xo nhẹ dao động điều hoà theo phương ngang với biên độ 4 cm thì chu kì là 0,8 s. Nếu cho vật dao động với biên độ 2 cm thì chu kì dao động điều hoà của vật là

1. 0,8 s
2. 0,4 s
3. 2 cm
4. 1,6 cm

Bài tập 7

Quả cầu m gắn vào lò xo có độ cứng k thì nó dao động với chu kì T. Hỏi phải cắt lò xo trên thành bao nhiêu phần bằng nhau để khi treo quả cầu vào mỗi phần thì chu kì dao động có giá trị T’ = T/2

1. Cắt làm 4 phần                B. Cắt làm 6 phần
2. C. Cắt làm 2 phần           D. Cắt làm 8 phần

Bài giải

Giả sử cắt lò xo thành n phần bằng nhau thì mỗi phần có độ cứng là n.k

Khi đó: T’ = 2π√(m/k) =T/√n= T/2

=> n = 4

Bài tập 8

Con lắc lò xo gồm vật nặng treo dưới cái lò xo dài, có chu kì dao động là T. Nếu lò xo bị cắt bớt 2/3 chiều dài thì chu kì dao động của con lắc mới là:

1. 3T     B. 0,5T√6     C. T/3     D. T/√3

Bài giải

Ta có: l’ = l/3

=> kl = k’l/3

=> k’ = 3k

Trong khi đó: T’ = 2π√(m/3k) = T/√3

Kết luận

Công thức tính chu kỳ được tổng hợp kèm theo bài tập vận dụng giúp bạn ghi nhớ lâu hơn. Chúc bạn ôn tập hiệu quả và đạt được kết quả cao trong kỳ thi sắp tới.