Công thức tính momen lực – Lý thuyết và bài tập hướng dẫn

Công thức tính momen lực phản ánh rõ nét chuyển động của vật thể dưới dạng quay trên một điểm hoặc một trục. Đây là khái niệm quan trọng trong bộ môn vật lý, mang tính ứng dụng thực tiễn cao.

Định nghĩa công thức tính momen lực là gì và ví dụ

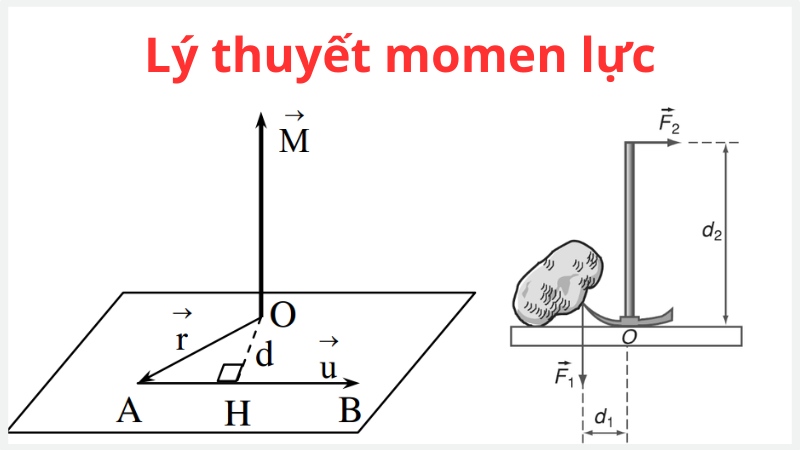
Công thức tính momen lực biểu thị mối liên hệ giữa lực tác động lên vật và cánh tay đòn. Nó được thể hiện dưới dạng M (momen lực) =  F x d, trong đó:

• Đơn vị của M là Nm;
• F là lực tác động lên vật với đơn vị là N;
• d là khoảng cách tính từ trục quay đến điểm tác động lực (hay còn gọi là cánh tay đòn), đơn vị là mét.

Từ công thức có thể hiểu đơn giản một Newton áp dụng lên một cánh tay đòn dài một mét có momen lực bằng bao nhiêu.

Muốn áp dụng công thức phải đảm bảo các điều kiện sau:

• Giá của lực và trục quay không cắt nhau, bởi nếu giá của lực đi qua tâm quay thì vật sẽ không thể qua được, M=0.
• Mặt phẳng chứa lực và trục quay phải vuông góc với nhau.

Nếu muốn tăng M thì có thể lựa chọn tăng F hoặc tăng d hoặc tăng cả hai đại lượng.

Ví dụ: Bạn có thể dễ dàng tìm thấy thực tiễn áp dụng công thức momen lực trong đời sống. Chẳng hạn khi mở cửa sổ, cánh tay đòn là khoảng cách từ bản lề đến tay cửa, còn lực tác động xác định trên cánh cửa sổ.

Lý thuyết cần nhớ về momen lực, công thức mở rộng

Công thức được xây dựng từ khái niệm momen lực trong vật lý học. Cụ thể, thuật ngữ này chỉ sự chuyển động của vật thể quanh một trục hoặc một điểm dưới dạng quay.

M (momen lực) sẽ tỉ lệ thuận với tích của độ lớn lực tác động với khoảng cách từ trục đến tâm của vật.

Khái niệm này được ứng dụng để mở rộng các công thức từ chuyển động thẳng thành quay lên một vật thể rắn.

Momen có thể xem là một vectơ (đoạn thẳng có hướng) với gốc G (trục) và tâm O (trên vật).

Để công thức tính momen lực chính xác, chuyển động của vật thể phải được tạo trên trục quay cố định.

Tổng momen lực tác động lên vật quay theo chiều kim đồng hồ phải bằng tổng momen lực tác động làm vật quay ngược chiều kim đồng hồ:

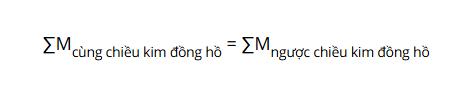
Tuy nhiên không phải lúc nào vật cũng phải đặt trên một trục quay và quay thì mới tạo ra momen lực. Quy tắc còn có thể áp dụng trong trường hợp không có trục ban đầu nhưng vì lý do nào đó, vật xuất hiện trục quay.

Nguồn gốc của momen lực và tính phát triển của công thức

Thuật ngữ này xuất hiện lần đầu khi nhà khoa học cổ đại Archimedes (Ác-si-mét) tìm ra nguyên lý hoạt động của đòn bẩy.

Theo ông, độ lớn của khả năng tác động lực lên đòn bẩy sẽ tỉ lệ thuận với độ lớn của lực và khoảng cách từ điểm tác dụng lực tới tâm quay.

Khoảng cách này chính là điểm mấu chốt trong hoạt động của đòn bẩy hay ròng rọc, được gọi là cánh tay đòn.

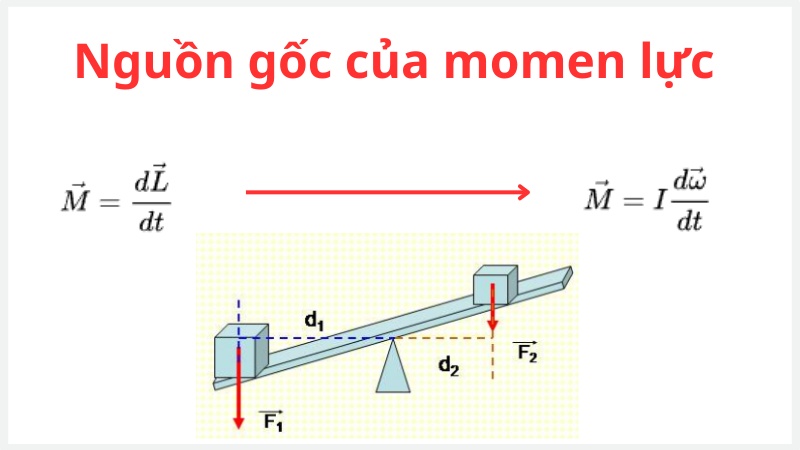
Khái niệm này có ảnh hưởng đến cả việc xác định momen động lượng sau này. Cụ thể nếu không có momen lực tác động lên vật, momen động lượng sẽ giữ nguyên không đổi theo thời gian.

Mối liên hệ này được biểu thị thông qua phương trình với sự kết hợp từ Định luật II Newton. Lưu ý là phương trình còn có thể phát triển nếu xác định được momen quán tính của vật không đổi.

Ứng dụng momen lực trong đời sống

• Cực kỳ phổ biến

Nếu để ý bạn sẽ thấy khái niệm này xuất hiện rất rộng rãi, từ cuộc sống đến sản xuất:

• Tối ưu thiết kế kỹ thuật: Sử dụng công thức momen lực để tạo nên các chuyển động từ vật có sẵn sao cho ít tốn sức nhất. Phổ biến nhất là thiết kế tay nắm cửa sao cho việc đóng mở dễ dàng, thuận tiện.
• Tính toán lực sao cho lớn hơn trọng lực của vật: Ứng dụng trong quá trình tạo ra ròng rọc, bánh răng, đòn bẩy, hoàn thiện chi tiết máy móc.
• Tạo ra công cụ phục vụ đời sống: Cờ lê chính là ví dụ điển hình của việc ứng dụng momen lực. Tức là khi tác động một lực nhỏ lên một đầu của dụng cụ này, momen lực sẽ được tạo ra ở đầu còn lại từ đó hỗ trợ việc tháo lắp hiệu quả.
• Kiểm tra độ bền của công trình xây dựng.
• Ứng dụng trong thiết kế robot: Mục đích chính là để tối ưu hoá hiệu suất hoạt động cũng như đảm bảo tính chính xác khi robot nâng vật, tác động lực lên vật hay hoàn thiện cấu trúc các bộ phận bên trong.

Bài tập áp dụng công thức tính momen lực và cách giải

Đề bài: Giả sử một thanh sắt CD có m = 50kg, chiều dài bằng 15 mét, khoảng cách từ trọng tâm G đến đầu C bằng 2,4m. Trục quay đi qua điểm O, thanh CD có thể quay quanh trục này với khoảng cách OC = 3m. Cho g = 20m/s2.

Khi tác động một lực lên đầu D, trục quay tác động lên thanh bằng một lực. Hãy xác định:

1. Giá trị của lực cần thiết để khi tác động lên D mà thanh vẫn cân bằng khi quay.
2. Giá trị của lực tác động từ trục quay lên thanh CD.

=> Cách giải: Để thanh nằm cân bằng thì momen lực G phải bằng momen lực D nghĩa là M(G) = M(B).

Ta có công thức: mg.GO = F.OD từ đó tính được F

• 25N.

Mà N = F + P nên cuối cùng tính được giá trị lực tác động từ trục quay lên thanh là 525N.

Kết luận

Công thức tính momen lực giúp bạn hiểu hơn về chuyển động quay của một vật và ứng dụng vào các trường hợp vật lý liên quan. Nếu muốn tìm hiểu thêm nhiều khái niệm khác trong bộ môn, bạn hãy truy cập website congthucvatly.org.